AI上推荐 之 MIND(动态路由与胶囊网络的奇光异彩)

1. 写在前面

今天整理的是MIND模型(Multi-Interest Network with Dynamic Routing)， 这是阿里团队2019年在CIKM上发的一篇paper，该模型依然是用在召回阶段的一个模型，解决的痛点是之前在召回阶段的模型，比如双塔，上一篇介绍的YouTubeDNN召回模型等，在模拟用户兴趣的时候，总是基于用户的历史点击，最后通过pooling的方式得到一个兴趣向量，用该向量来表示用户的兴趣，但是该篇论文的作者认为，用一个向量来表示用户的广泛兴趣未免有点太过于单一，这是作者基于天猫的实际场景出发的发现，每个用户每天与数百种产品互动， 而互动的产品往往来自于很多个类别，这就说明用户的兴趣极其广泛，用一个向量是无法表示这样广泛的兴趣的，当然，即使能，向量的维度也会很大，会带来计算上的压力，于是乎，就自然而然的引出一个问题，有没有可能用多个向量来表示用户的多种兴趣呢？ 如果这个问题交给我们想，我们应该也能想到解决方法，既然用户交互的历史商品很多，又来自不同的种类，那么我们完全可以对这些历史商品先聚类，然后每一类里面的商品进行pooling，不就得到多个向量来表示用户的多个兴趣了？

读完这篇paper之后，我感觉作者思考出发点应该也是这样，但是人家用了一种更加优雅的方式对用户交互过的历史商品进行聚类，即胶囊网络，该网络采用了动态路由算法能非常自然的将历史商品聚成多个集合，每个集合的历史行为进一步推断对应特定兴趣的用户表示向量。这样，对于一个特定的用户，MND输出了多个表示向量，它们代表了用户的不同兴趣。当用户再有新的交互时，通过胶囊网络，还能实时的改变用户的兴趣表示向量，做到在召回阶段的实时个性化。所以这个机制还是非常powerful的，那么，胶囊网络究竟是怎么做到的呢？ 胶囊网络又是什么原理呢？这篇文章来剖析下

首先，还是按照论文的逻辑，在Introduction部分介绍下该模型提出的动机，以及之前的一些召回模型有什么问题，然后介绍胶囊网络及相关知识，因为MIND模型的核心就是多兴趣提取层，而这个层其实就是一个胶囊网络结合实际情况的改进版本，所以我觉得如果想理解这个核心层，胶囊网络必须先有个认识，但论文里面介绍胶囊网络直接上了很多复杂公式，并不是很直观易懂，不符合我总结论文的风格，所以我想先拿出一小节，单独介绍下胶囊网络，这个东西也是非常有意思，其实一开始是为了解决CNN的pooling痛点提出的，竟然也能用到推荐里面，所以，知识是一通百通，而如果我们多了解其他领域的一些东西，有时候idea就来了哈哈，有了这一小节铺垫，就会发现这篇论文读起来简单清晰了。 接下来就是MIND的网络架构，进行各层的细节剖析，最后就是基于新闻推荐数据集简单实现下MIND，跑下召回看看效果，从代码层面再深入了解下。

PS： 这篇文章依然会很长，还是各取所需即可

主要内容：

• 背景与动机
• 胶囊网络与动态路由机制
• MIND模型的网络结构与细节剖析
• MIND模型之简易代码复现
• MIND模型在deepmatch中的使用方法
• 总结

Ok, let’s go!

2. 背景与动机

本章是基于天猫APP的背景来探索十亿级别的用户个性化推荐。天猫的推荐的流程主要分为召回阶段和排序阶段。召回阶段负责检索数千个与用户兴趣相关的候选物品，之后，排序阶段预测用户与这些候选物品交互的精确概率。这篇文章做的是召回阶段的工作，来对满足用户兴趣的物品的有效检索。

作者这次的出发点是基于场景出发，在天猫的推荐场景中，作者发现用户的兴趣存在多样性。平均上，10亿用户访问天猫，每个用户每天与数百种产品互动。交互后的物品往往属于不同的类别，说明用户兴趣的多样性。 一张图片会更加简洁直观：

因此如果能在召回阶段建立用户多兴趣模型来模拟用户的这种广泛兴趣，那么作者认为是非常有必要的，因为召回阶段的任务就是根据用户兴趣检索候选商品嘛。

那么，如何能基于用户的历史交互来学习用户的兴趣表示呢？ 以往的解决方案如下：

• 协同过滤的召回方法(itemcf和usercf)是通过历史交互过的物品或隐藏因子直接表示用户兴趣， 但会遇到稀疏或计算问题
• 基于深度学习的方法用低维的embedding向量表示用户，比如YoutubeDNN召回模型，双塔模型等，都是把用户的基本信息，或者用户交互过的历史商品信息等，过一个全连接层，最后编码成一个向量，用这个向量来表示用户兴趣，但作者认为，这是多兴趣表示的瓶颈，因为需要压缩所有与用户多兴趣相关的信息到一个表示向量，所有用户多兴趣的信息进行了混合，导致这种多兴趣并无法体现，所以往往召回回来的商品并不是很准确，除非向量维度很大，但是大维度又会带来高计算。
• DIN模型在Embedding的基础上加入了Attention机制，来选择的捕捉用户兴趣的多样性，但采用Attention机制，对于每个目标物品，都需要重新计算用户表示，这在召回阶段是行不通的(海量)，所以DIN一般是用于排序。不过，从另一个角度看，我现在觉得其实MIND和DIN很像，DIN无非是通过注意力机制，每次选择与当前商品相关的行为进行训练，而MIND首先是先把历史行为聚成多个类表示用户兴趣，然后通过注意力机制选择与当前商品相关的兴趣，但是，MIND最后能得到用户的多兴趣表示向量，而DIN不能，不过，在计算复杂度上我倒是觉得MIND并没有比DIN简洁多少，甚至可能更复杂，毕竟胶囊网络那里还得经历好几次迭代。

所以，作者想在召回阶段去建模用户的多兴趣，但以往的方法都不好使，为了解决这个问题，就提出了动态路由的多兴趣网络MIND。为了推断出用户的多兴趣表示，提出了一个多兴趣提取层，该层使用动态路由机制自动的能将用户的历史行为聚类，然后每个类簇中产生一个表示向量，这个向量能代表用户某种特定的兴趣，而多个类簇的多个向量合起来，就能表示用户广泛的兴趣了。

这就是MIND的提出动机以及初步思路了，这里面的核心是Multi-interest extractor layer， 而这里面重点是动态路由与胶囊网络，所以接下来先补充这方面的相关知识。

3. 胶囊网络与动态路由机制

3.1 胶囊网络初识

Hinton大佬在2011年的时候，就首次提出了"胶囊"的概念， "胶囊"可以看成是一组聚合起来输出整个向量的小神经元组合，这个向量的每个维度(每个小神经元)，代表着某个实体的某个特征。而真正介绍胶囊网络和动态路由的是Hinton在2017年的一篇paper，详细的可以来这里。

当然，由于篇幅原因，这里就不解读这篇文章了，而是用一种通俗易懂的方式来说明胶囊网络以及动态路由的原理说清楚就行了，这里我参考的李宏毅老师在B站上的胶囊网络课程，图片也来自李老师的PPT，所以详细的可以看这个教程，链接在参考出。

胶囊网络其实可以和神经网络对比着看可能更好理解，我们知道神经网络的每一层的神经元输出的是单个的标量值，接收的输入，也是多个标量值，所以这是一种value to value的形式，而胶囊网络每一层的胶囊输出的是一个向量值，接收的输入也是多个向量，所以它是vector to vector形式的。来个图对比下就清楚了：

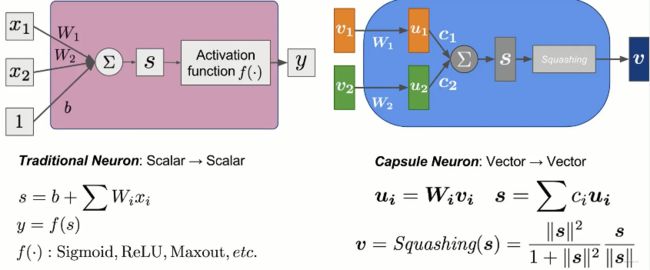
左边的图是普通神经元的计算示意，而右边是一个胶囊内部的计算示意图。 神经元这里不过多解释，这里主要是剖析右边的这个胶囊计算原理。从上图可以看出， 输入是两个向量$v_1,v_2$，首先经过了一个线性映射，得到了两个新向量$u_1,u_2$，然后呢，经过了一个向量的加权汇总，这里的$c_1$,$c_2$可以先理解成权重，具体计算后面会解释。 得到汇总后的向量$s$，接下来进行了Squash操作，整体的计算公式如下：
$$\begin{array}{rl}& u^1=W^1{v}^1{u}^2=W^2{v}^2\\ & s=c_1{u}^1+c_2{u}^2\\ & v=\mathrm{Squash}(s)=\frac{\Vert s{\Vert }^2}{1+\Vert s{\Vert }^2}\frac{s}{\Vert s\Vert }\end{array}$$
这里的Squash操作可以简单看下，主要包括两部分，右边的那部分其实就是向量归一化操作，把norm弄成1，而左边那部分算是一个非线性操作，如果$s$的norm很大，那么这个整体就接近1， 而如果这个norm很小，那么整体就会接近0， 和sigmoid很像有没有？

这样就完成了一个胶囊的计算，但有两点需要注意：

1. 这里的$W^i$参数是可学习的，和神经网络一样， 通过BP算法更新
2. 这里的$c_i$参数不是BP算法学习出来的，而是采用动态路由机制现场算出来的，这个非常类似于pooling层，我们知道pooling层的参数也不是学习的，而是根据前面的输入现场取最大或者平均计算得到的。

所以这里的问题，就是怎么通过动态路由机制得到$c_i$，下面是动态路由机制的过程。

3.2 动态路由机制原理

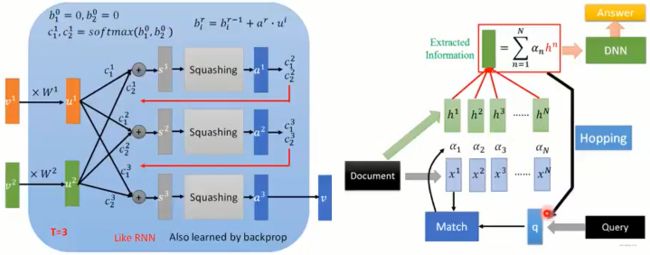
我们先来一个胶囊结构:

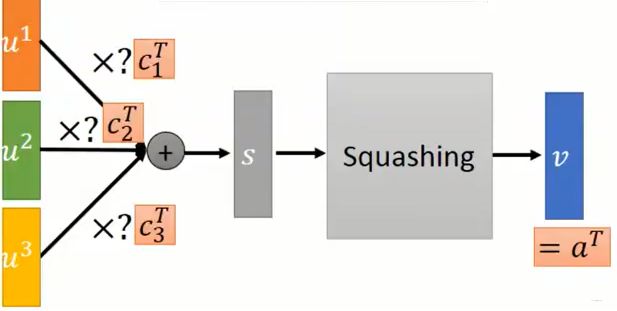
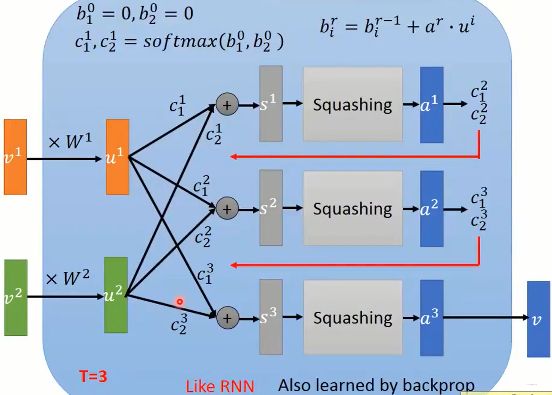
这个$c_i$是通过动态路由机制计算得到，那么动态路由机制究竟是啥子意思？ 其实就是通过迭代的方式去计算，没有啥神秘的，迭代计算的流程如下图:

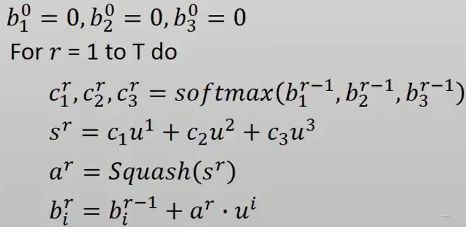
首先我们先初始化$b_i$，与每一个输入胶囊$u_i$进行对应，这哥们有个名字叫做"routing logit"， 表示的是输出的这个胶囊与输入胶囊的相关性，和注意力机制里面的score值非常像。由于一开始不知道这个哪个胶囊与输出的胶囊有关系，所以默认相关性分数都一样，然后进入迭代。

在每一次迭代中，首先把分数转成权重，然后加权求和得到$s$，这个很类似于注意力机制的步骤，得到$s$之后，通过归一化操作，得到$a$，接下来要通过$a$和输入胶囊的相关性以及上一轮的$b_i$来更新$b_i$。最后那个公式有必要说一下在干嘛：

如果当前的$a$与某一个输入胶囊$u_i$非常相关，即内积结果很大的话，那么相应的下一轮的该输入胶囊对应的$b_i$就会变大， 那么， 在计算下一轮的$a$的时候，与上一轮$a$相关的$u_i$就会占主导，相当于下一轮的$a$与上一轮中和他相关的那些$u_i$之间的路径权重会大一些，这样从空间点的角度观察，就相当于$a$点朝与它相关的那些$u$点更近了一点。

通过若干次迭代之后，得到最后的输出胶囊向量$a$会慢慢的走到与它更相关的那些$u$附近，而远离那些与它不相干的$u$。所以上面的这个迭代过程有点像排除异常输入胶囊的感觉。

而从另一个角度来考虑，这个过程其实像是聚类的过程，因为胶囊的输出向量$v$经过若干次迭代之后，会最终停留到与其非常相关的那些输入胶囊里面，而这些输入胶囊，其实就可以看成是某个类别了，因为既然都共同的和输出胶囊$v$比较相关，那么彼此之间的相关性也比较大，于是乎，经过这样一个动态路由机制之后，就不自觉的，把输入胶囊实现了聚类。把和与其他输入胶囊不同的那些胶囊给排除了出去。

所以，这个动态路由机制的计算设计的还是比较巧妙的， 下面是上述过程的展开计算过程， 这个和RNN的计算有点类似：

这样就完成了一个胶囊内部的计算过程了。

3.3 Why? 胶囊网络会work呢？

首先，先了解下胶囊网络提出的动机，这东西其实一开始是想要解决CNN在图像方面存在的问题的。

CNN的问题源自对图像感知的泛化能力，比如一个训练好的CNN可能对同一个图像的旋转版本会识别错误，这就是为啥会使用数据增强以及pooling的操作去增加鲁棒程度：

• pooling操作可以随机选上一层神经元子集，使得网络减少对特征出现的原始位置的依赖
• 数据增强则是先给图片经过各种旋转，裁剪，变换等操作，让CNN能看到同一张图片不同的这些形态

但这两种策略的依据在于： 特征出现的确切位置对目标识别而言影响不大。但池化的这种操作，依然会丢弃掉目标物体的准确位置信息。

而胶囊网络赋予了模型理解图像中所发生变化的能力，从而可以更好地概括所感知的内容。这使得模型对图像中的细微变化可以保持不变的输出。 另一方面，模型有可能忽视图像发生的位移变化。不变意味着无论检测到的字符的顺序和位置是否改变，网络的输出总是相同的。 因此该模型能够理解图像中的特征的旋转和位移，并产生适当的输出。 对于使用池化来说是不可能的。 这就是启发我们发明这个新架构的原因。

如果上面不好理解，下面从手写数字识别的这个例子来看。

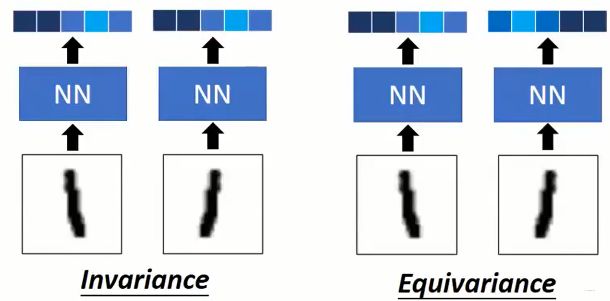
从"Invariance"和"Equivariance"的角度理解，我们说CNN是"Invariance"的，因为我们输入两种1，其实右边的1是翻转版本，但对于CNN来讲，最终的识别都是1，并没有啥区别，即左边图，输入的两个1，过CNN之后得到的两个向量会一样，这叫做"Invariance"，即只认识1，但不知道这俩个1有啥区别。 右边图是"Equivariance"，意思是我这两个1过网络，希望得到的是两个不同的向量，虽然最后分类的时候，依然是认识1，但是我希望能通过这两个不同的向量能区分出输入两个1的区别，一个是翻转了的，一个没翻转，有没有可能学习到这样的一个区别？

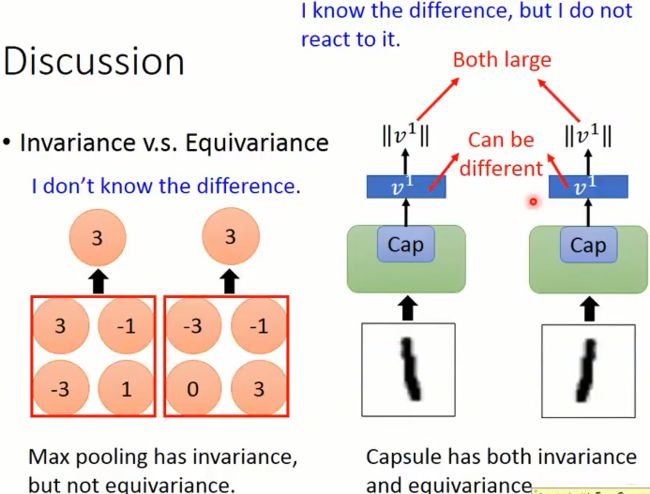
CNN中的池化操作呢，只能做到Invariance，因为不管输入的上一层神经元的位置如何，我都是取最大或者取平均，这样是看不出差异来的。 而胶囊网络呢，就有了invariance和equivariance的能力，胶囊网络最终的输出是一个向量， 这个向量的每一个维度，其实就是表示了图片或者输入对象在某些方面的特性，比如是否旋转，亮度，颜色等。 这样最后虽然也是能正确识别数字，但至少知道区别，只不过不去关注罢了。所以胶囊网络是个“装糊涂的高手”，能够比普通的CNN获取更多的图像信息，所以在图像处理任务上据说更加鲁棒。

其实胶囊网络很像很像注意力机制：

3.4 带有卷积的胶囊网络

上面其实已经把胶囊网络和动态路由机制整理完了，这里只是记录下我学这块的一个好奇， 就是在上面如何用胶囊网络做手写数字图像识别？ 又是如何学习图像之间的空间关系的呢？李宏毅老师讲课的PPT中这样解释做手写数字图像识别，但是我其实好奇CapsNet这个部分到底是咋做的，胶囊在这里面长的什么样子。

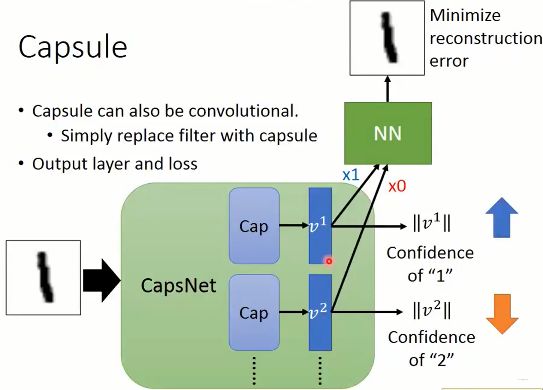
所以就找了一些其他的文章，差不多能解决我的疑问了，原来胶囊网络里面也是有卷积操作的，只不过卷积完了之后，往往会创建一个胶囊操作，like this:

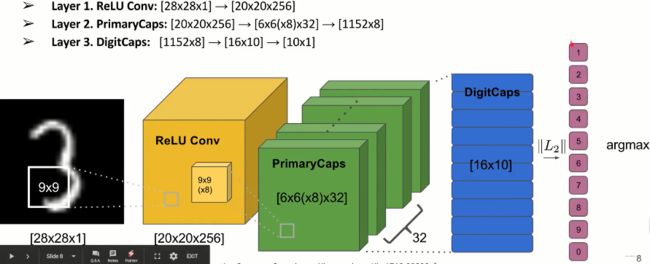
首先，依然是会相同一个卷积操作， 得到像素点之间的局部关联，然后将卷积之后的特征图经过reshape就得到了胶囊，这里比如卷积时候的输出特征图是$20\times 20\times 256$，经过一个Reshape操作，变成$6\times 6\times 8\times 32$， 这里的$8$就是每一个胶囊的向量维度，胶囊的个数是$6\times 6\times 32$个，这里如果是代码的话会更好解释些，其实就是个这样的操作

conv = tf.contrib.layers.conv2d(input_layer, N * C, kernel, stride, padding="VALID")
# Shape: (?, T, T, N * C)

capsules = tf.reshape(conv, shape=(-1, T*T*N, C, 1))
# Shape: (?, T*T*N, C, 1)

# conv[0][0][0][:C] <=> capsules[0]

然后我们得到$T\ast T\ast N$个大小为$C$的胶囊（在这个项目中是$6\times 6\times 32=1152$个胶囊）。 需要指出的是，卷积的第一个C值（见代码中的注释）等于第一个胶囊的值，正如上面代码所示。这个看绿色的那个图会很好理解，conv[0][0][0]就是最左上角的那一长串像素点，共N*C个值，正好是N个胶囊，第0个胶囊就是conv[0][0][0][:C]，这样就得到了胶囊，接下来，就对每个胶囊squash操作。就可以作为下一层的输入了。 接下来，就是把这些胶囊横着排放在一块，得到了$1152\times 8$的矩阵了，这1152 个胶囊作为下一层胶囊网络的输入，下一层网络层的输出胶囊个数是10个， 每一个胶囊的维度是16，对于每个胶囊的运算，1152个输入胶囊，分别做线性映射，即乘一个$8\times 16$的矩阵，得到了1152个$1\times 16$的向量，然后这些向量进行10次动态路由操作，就得到了10个16维的向量，即下一层的输出。这10个16维的向量，求norm，label是哪个就希望哪个输出的norm最大。当然也可以拼起来再接NN求损失等，这就是整个过程了。

Ok， 有了上面的这些铺垫，再来看MIND就会比较简单了。下面正式对MIND模型的网络架构剖析。

4. MIND模型的网络结构与细节剖析

4.1 网络整体结构

MIND网络的架构如下：

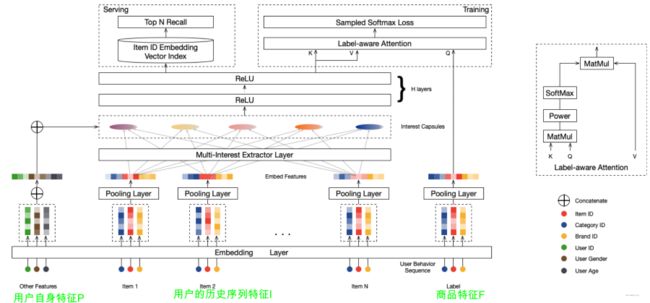
初步先分析这个网络结构的运作： 首先接收的输入有三类特征，用户base属性，历史行为属性以及商品的属性，用户的历史行为序列属性过了一个多兴趣提取层得到了多个兴趣胶囊，接下来和用户base属性拼接过DNN，得到了交互之后的用户兴趣。然后在训练阶段，用户兴趣和当前商品向量过一个label-aware attention，然后求softmax损失。 在服务阶段，得到用户的向量之后，就可以直接进行近邻检索，找候选商品了。 这就是宏观过程，但是，多兴趣提取层以及这个label-aware attention是在做什么事情呢？ 如果单独看这个图，感觉得到多个兴趣胶囊之后，直接把这些兴趣胶囊以及用户的base属性拼接过全连接，那最终不就成了一个用户向量，此时label-aware attention的意义不就没了？ 所以这个图初步感觉画的有问题，和论文里面描述的不符。所以下面先以论文为主，正式开始描述具体细节。

4.2 任务目标

召回任务的目标是对于每一个用户$u\in \mathcal{U}$从十亿规模的物品池$\mathcal{I}$检索出包含与用户兴趣相关的上千个物品集。

4.2.1 模型的输入

对于模型，每个样本的输入可以表示为一个三元组：$\left({\mathcal{I}}_u,{\mathcal{P}}_u,{\mathcal{F}}_i\right)$，其中${\mathcal{I}}_u$代表与用户$u$交互过的物品集，即用户的历史行为；${\mathcal{P}}_u$表示用户的属性，例如性别、年龄等；${\mathcal{F}}_i$定义为目标物品$i$的一些特征，例如物品id和种类id等。

4.2.2 任务描述

MIND的核心任务是学习一个从原生特征映射到用户表示的函数，用户表示定义为：
$${\mathrm{V}}_u=f_{user}\left({\mathcal{I}}_u,{\mathcal{P}}_u\right)$$
其中，${\mathbf{V}}_u=\left({\mathbf{v}}_u^1,\dots ,{\mathbf{v}}_u^K\right)\in {\mathbb{R}}^{d\times k}$是用户$u$的表示向量，$d$是embedding的维度，$K$表示向量的个数，即兴趣的数量。如果$K=1$，那么MIND模型就退化成YouTubeDNN的向量表示方式了。

目标物品$i$的embedding函数为：
$${\mathbf{e}}_i=f_{\text{item }}\left({\mathcal{F}}_i\right)$$
其中，${\mathbf{e}}_i\in {\mathbb{R}}^{d\times 1},f_{item}(\cdot )$表示一个embedding&pooling层。

4.2.3 最终结果

根据评分函数检索（根据目标物品与用户表示向量的内积的最大值作为相似度依据，DIN的Attention部分也是以这种方式来衡量两者的相似度），得到top N个候选项：

$$f_{\text{score }}\left({\mathbf{V}}_u,{\mathbf{e}}_i\right)=\underset{1\le k\le K}{\max }{\mathbf{e}}_i^{\mathrm{T}}{\mathbf{V}}_u^{\mathrm{k}}$$

4.3 Embedding & Pooling层

Embedding层的输入由三部分组成，用户属性${\mathcal{P}}_u$、用户行为${\mathcal{I}}_u$和目标物品标签${\mathcal{F}}_i$。每一部分都由多个id特征组成，则是一个高维的稀疏数据，因此需要Embedding技术将其映射为低维密集向量。具体来说，

• 对于${\mathcal{P}}_u$的id特征（年龄、性别等）是将其Embedding的向量进行Concat，组成用户属性Embedding${\mathbf{p}}_u$；
• 目标物品${\mathcal{F}}_i$通常包含其他分类特征id（品牌id、店铺id等） ，这些特征有利于物品的冷启动问题，需要将所有的分类特征的Embedding向量进行平均池化，得到一个目标物品向量${\mathbf{e}}_i$；
• 对于用户行为${\mathcal{I}}_u$，由物品的Embedding向量组成用户行为Embedding列表$E_u={\mathbf{e}}_j,j\in {\mathcal{I}}_u$， 当然这里不仅只有物品embedding哈，也可能有类别，品牌等其他的embedding信息。

4.4 Multi-Interest Extractor Layer(核心)

作者认为，单一的向量不足以表达用户的多兴趣

所以作者采用多个表示向量来分别表示用户不同的兴趣。通过这个方式，在召回阶段，用户的多兴趣可以分别考虑，对于兴趣的每一个方面，能够更精确的进行物品检索。

为了学习多兴趣表示，作者利用胶囊网络表示学习的动态路由将用户的历史行为分组到多个簇中。来自一个簇的物品应该密切相关，并共同代表用户兴趣的一个特定方面。

由于多兴趣提取器层的设计灵感来自于胶囊网络表示学习的动态路由，所以这里作者回顾了动态路由机制。当然，如果之前对胶囊网络或动态路由不了解，这里读起来就会有点艰难，但由于我上面进行了铺垫，这里就直接拿过原文并解释即可。

4.4.1 动态路由

动态路由是胶囊网络中的迭代学习算法，用于学习低水平胶囊和高水平胶囊之间的路由对数（logit）$b_{ij}$，来得到高水平胶囊的表示。

我们假设胶囊网络有两层，即低水平胶囊$c_i^l\in {\mathbb{R}}^{N_l\times 1},i\in \{1,\dots ,m\}$和高水平胶囊$c_j^h\in {\mathbb{R}}^{N_h\times 1},j\in \{1,\dots ,n\}$，其中$m,n$表示胶囊的个数， $N_l,N_h$表示胶囊的维度。 路由对数$b_{ij}$计算公式如下：
$$b_{ij}={\left(c_j^h\right)}^T{\mathrm{S}}_{ij}{c}_i^l$$
其中${\mathbf{S}}_{ij}\in {\mathbb{R}}^{N_h\times N_l}$表示待学习的双线性映射矩阵【在胶囊网络的原文中称为转换矩阵】

通过计算路由对数，将高阶胶囊$j$的候选向量计算为所有低阶胶囊的加权和：
$$z_j^h=\sum _{i=1}^m{w}_{ij}{S}_{ij}{c}_i^l$$
其中$w_{ij}$定义为连接低阶胶囊$i$和高阶胶囊$j$的权重【称为耦合系数】，而且其通过对路由对数执行softmax来计算：
$$w_{ij}=\frac{\exp b_{ij}}{{\sum }_{k=1}^m\exp b_{ik}}$$
最后，应用一个非线性的“压缩”函数来获得一个高阶胶囊的向量【胶囊网络向量的模表示由胶囊所代表的实体存在的概率】
$$c_j^h=\mathrm{squash}\left(z_j^h\right)=\frac{{\Vert z_j^h\Vert }^2}{1+{\Vert z_j^h\Vert }^2}\frac{z_j^h}{\Vert z_j^h\Vert }$$
路由过程重复进行3次达到收敛。当路由结束，高阶胶囊值$c_j^h$固定，作为下一层的输入。

Ok，下面我们开始解释，其实上面说的这些就是胶囊网络的计算过程，只不过和之前所用的符号不一样了。这里拿个图：

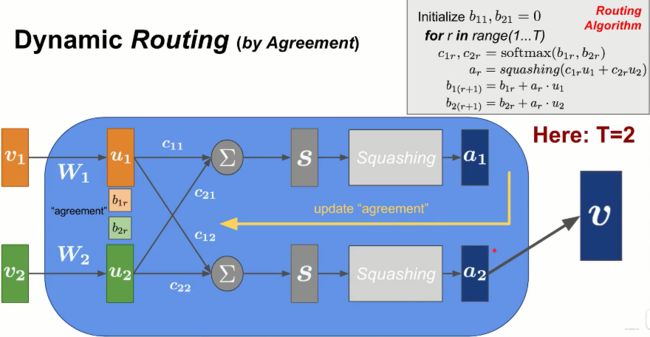
首先，论文里面也是个两层的胶囊网络，低水平层->高水平层。 低水平层有$m$个胶囊，每个胶囊向量维度是$N_l$，用$c_i^l$表示的，高水平层有$n$个胶囊，每个胶囊$N_h$维，用$c_j^h$表示。

单独拿出每个$c_j^h$，其计算过程如上图所示。首先，先随机初始化路由对数$b_{ij}=0$，然后开始迭代，对于每次迭代：
$$\begin{gathered} w_{ij}=\frac{\exp b_{ij}}{{\sum }_{k=1}^m\exp b_{ik}} \\ {z}_j^h=\sum _{i=1}^m{w}_{ij}{S}_{ij}{c}_i^l \\ {c}_j^h=\mathrm{squash}\left(z_j^h\right)=\frac{{\Vert z_j^h\Vert }^2}{1+{\Vert z_j^h\Vert }^2}\frac{z_j^h}{\Vert z_j^h\Vert } \\ {b}_{ij}={\left(c_j^h\right)}^T{\mathrm{S}}_{ij}{c}_i^l \end{gathered}$$
只不过这里的符合和上图中的不太一样，这里的$w_{ij}$对应的是每个输入胶囊的权重$c_{ij}$， 这里的$c_j^h$对应上图中的$a$， 这里的$z_j^h$对应的是输入胶囊的加权组合。这里的$c_i^l$对应上图中的$v_i$，这里的$S_{ij}$对应的是上图的权重$W_{ij}$，只不过这个可以换成矩阵运算。 和上图中不同的是路由对数$b_{ij}$更新那里，没有了上一层的路由对数值，但感觉这样会有问题。

所以，这样解释完之后就会发现，其实上面的一顿操作就是说的传统的动态路由机制。

4.4.2 B2I动态路由

作者设计的多兴趣提取层就是就是受到了上述胶囊网络的启发

如果把用户的行为序列看成是行为胶囊， 把用户的多兴趣看成兴趣胶囊，那么多兴趣提取层就是利用动态路由机制学习行为胶囊->兴趣胶囊的映射关系。但是原始路由算法无法直接应用于处理用户行为数据。因此，提出了行为(Behavior)到兴趣(Interest)（B2I）动态路由来自适应地将用户的行为聚合到兴趣表示向量中，它与原始路由算法有三个不同之处：

1. 共享双向映射矩阵。在初始动态路由中，使用固定的或者说共享的双线性映射矩阵$S$而不是单独的双线性映射矩阵， 在原始的动态路由中，对于每个输出胶囊$c_j^h$，都会有对应的$S_{ij}$，而这里是每个输出胶囊，都共用一个$S$矩阵。 原因有两个：

   1. 一方面，用户行为是可变长度的，从几十个到几百个不等，因此使用共享的双线性映射矩阵是有利于泛化。
   2. 另一方面，希望兴趣胶囊在同一个向量空间中，但不同的双线性映射矩阵将兴趣胶囊映射到不同的向量空间中。因为映射矩阵的作用就是对用户的行为胶囊进行线性映射嘛， 由于用户的行为序列都是商品，所以希望经过映射之后，到统一的商品向量空间中去。路由对数计算如下：
      $$b_{ij}={\mathbf{u}}_j^T{\mathrm{S}\mathrm{e}}_i,i\in {\mathcal{I}}_u,j\in \{1,\dots ,K\}$$
      其中，${\mathbf{e}}_i\in {\mathbb{R}}^d$是历史物品$i$的embedding，$u_j\in {\mathbb{R}}^d$表示兴趣胶囊$j$的向量。$S\in {\mathbb{R}}^{d\times d}$是每一对行为胶囊(低价)到兴趣胶囊(高阶)之间的共享映射矩阵。

2. 随机初始化路由对数。由于利用共享双向映射矩阵$S$，如果再初始化路由对数为0将导致相同的初始的兴趣胶囊。随后的迭代将陷入到一个不同兴趣胶囊在所有的时间保持相同的情景。因为每个输出胶囊的运算都一样了嘛(除非迭代的次数不同，但这样也会导致兴趣胶囊都很类似)，为了减轻这种现象，作者通过高斯分布进行随机采样来初始化路由对数$b_{ij}$，让初始兴趣胶囊与其他每一个不同，其实就是希望在计算每个输出胶囊的时候，通过随机化的方式，希望这几个聚类中心离得远一点，这样才能表示出广泛的用户兴趣(我们已经了解这个机制就仿佛是聚类，而计算过程就是寻找聚类中心)。

3. 动态的兴趣数量，兴趣数量就是聚类中心的个数，由于不同用户的历史行为序列不同，那么相应的，其兴趣胶囊有可能也不一样多，所以这里使用了一种启发式方式自适应调整聚类中心的数量，即$K$值。
   $$K_u^{\prime }=\max \left(1,\min \left(K,{\log }_2\left(\left|{\mathcal{I}}_u\right|\right)\right)\right)$$
   这种调整兴趣胶囊数量的策略可以为兴趣较小的用户节省一些资源，包括计算和内存资源。这个公式不用多解释，与行为序列长度成正比。

最终的B2I动态路由算法如下：

应该很好理解了吧，不解释了。

4.5 Label-aware Attention Layer

通过多兴趣提取器层，从用户的行为embedding中生成多个兴趣胶囊。不同的兴趣胶囊代表用户兴趣的不同方面，相应的兴趣胶囊用于评估用户对特定类别的偏好。所以，在训练的期间，最后需要设置一个Label-aware的注意力层，对于当前的商品，根据相关性选择最相关的兴趣胶囊。这里其实就是一个普通的注意力机制，和DIN里面的那个注意力层基本上是一模一样，计算公式如下：
$$\begin{array}{rl}{\mathbf{v}}_u& =\mathrm{Attention}\left({\mathbf{e}}_i,{\mathrm{V}}_u,{\mathrm{V}}_u\right)\\ & ={\mathrm{V}}_u\mathrm{softmax}\left(\mathrm{pow}\left({\mathrm{V}}_u^{\mathrm{T}}{\mathbf{e}}_i,p\right)\right)\end{array}$$
首先这里的${\mathbf{e}}_i$表示当前的商品向量，$V_u$表示用户的多兴趣向量组合，里面有$K$个向量，表示用户的$K$的兴趣。用户的各个兴趣向量与目标商品做内积，然后softmax转成权重，然后反乘到多个兴趣向量进行加权求和。 但是这里需要注意的一个小点，就是这里做内积求完相似性之后，先做了一个指数操作，这个操作其实能放大或缩小相似程度，至于放大或者缩小的程度，由$p$控制。 比如某个兴趣向量与当前商品非常相似，那么再进行指数操作之后，如果$p$也很大，那么显然这个兴趣向量就占了主导作用。$p$是一个可调节的参数来调整注意力分布。当$p$接近0，每一个兴趣胶囊都得到相同的关注。当$p$大于1时，随着$p$的增加，具有较大值的点积将获得越来越多的权重。考虑极限情况，当$p$趋近于无穷大时，注意机制就变成了一种硬注意，选关注最大的值而忽略其他值。在实验中，发现使用硬注意导致更快的收敛。

理解：$p$小意味着所有的相似程度都缩小了， 使得之间的差距会变小，所以相当于每个胶囊都会受到关注，而越大的话，使得各个相似性差距拉大，相似程度越大的会更大，就类似于贫富差距， 最终使得只关注于比较大的胶囊。

4.6 训练与服务

得到用户向量${\mathbf{v}}_u$和标签物品embedding$e_i$后，计算用户$u$与标签物品$i$交互的概率：
$$\mathrm{Pr}(i\mid u)=\mathrm{Pr}\left(e_i\mid v_u\right)=\frac{\exp \left(v_u^{\mathrm{T}\to }\right)}{{\sum }_{j\in I}\exp \left(v_u^{\mathrm{T}}{e}_j\right)}$$
目标函数是：
$$L=\sum _{(u,i)\in \mathcal{D}}\log \mathrm{Pr}(i\mid u)$$
其中$\mathcal{D}$是训练数据包含用户物品交互的集合。因为物品的数量可伸缩到数十亿，所以不能直接算。因此。使用采样的softmax技术，并且选择Adam优化来训练MIND。

训练结束后，抛开label-aware注意力层，MIND网络得到一个用户表示映射函数$f_{user}$。在服务期间，用户的历史序列与自身属性喂入到$f_{user}$，每个用户得到多兴趣向量。然后这个表示向量通过一个近似邻近方法来检索top N物品。

这就是整个MIND模型的细节了。

关于实验部分，由于这次比较常规，没发现大的tricks， 有个label-aware里面的$p$， 当趋于无穷大的时候， MIND的收敛更快，性能更好。 具体实验的时候可以试一下。

5. MIND模型之简易代码复现

下面参考Deepctr，用简易的代码实现下MIND，并在新闻推荐的数据集上进行召回任务。

关于数据集这里就不过多介绍了，可以参考我上一篇写的YoutubeDNN这篇文章 ， 这里的话，我们就直接看MIND模型的实现，解释下代码部分。

因为在上面介绍的时候，也是有几个小疑问的，比如胶囊网络怎么实现的？ 多兴趣提取层得到多个胶囊之后，与用户的基础特征过DNN，那么这时候得到的用户向量是一个嘛，那这样的话后面还做什么label-aware? label-aware又是怎么做的？

带着这几个小疑问，我们开始看代码，MIND代码相对于YouTubeDNN还是稍微有些复杂的，也花了我将近一天的时间才复现出来，但收获还是蛮多的，分享给大家，当然，可能有些是基于我目前的理解，不一定对。

5.1 整个代码架构

整个MIND模型，我是这么实现的，算是参考deepmatch修改的一个简易版本：

def MIND(user_feature_columns, item_feature_columns, num_sampled=5, k_max=2, p=1.0, dynamic_k=False, user_dnn_hidden_units=(64, 32),
        dnn_activation='relu', dnn_use_bn=False, l2_reg_dnn=0, l2_reg_embedding=1e-6, dnn_dropout=0, output_activation='linear', seed=1024):
    """
        :param k_max: 用户兴趣胶囊的最大个数
    """
    # 目前这里只支持item_feature_columns为1的情况，即只能转入item_id
    if len(item_feature_columns) > 1:
        raise ValueError("Now MIND only support 1 item feature like item_id")
    
    # 获取item相关的配置参数
    item_feature_column = item_feature_columns[0]
    item_feature_name = item_feature_column.name
    item_vocabulary_size = item_feature_column.vocabulary_size
    item_embedding_dim = item_feature_column.embedding_dim
    
    behavior_feature_list = [item_feature_name]
    
    # 为用户特征创建Input层
    user_input_layer_dict = build_input_layers(user_feature_columns)
    item_input_layer_dict = build_input_layers(item_feature_columns)
    # 将Input层转化成列表的形式作为model的输入
    user_input_layers = list(user_input_layer_dict.values())
    item_input_layers = list(item_input_layer_dict.values())
    
    # 筛选出特征中的sparse特征和dense特征，方便单独处理
    sparse_feature_columns = list(filter(lambda x: isinstance(x, SparseFeat), user_feature_columns)) if user_feature_columns else []
    dense_feature_columns = list(filter(lambda x: isinstance(x, DenseFeat), user_feature_columns)) if user_feature_columns else []
    varlen_feature_columns = list(filter(lambda x: isinstance(x, VarLenSparseFeat), user_feature_columns)) if user_feature_columns else []
    
    # 由于这个变长序列里面只有历史点击文章，没有类别啥的，所以这里直接可以用varlen_feature_columns
    # deepctr这里单独把点击文章这个放到了history_feature_columns
    seq_max_len = varlen_feature_columns[0].maxlen
    
    # 构建embedding字典
    embedding_layer_dict = build_embedding_layers(user_feature_columns+item_feature_columns)
    
    # 获取当前的行为特征(doc)的embedding，这里面可能又多个类别特征，所以需要pooling下
    query_embed_list = embedding_lookup(behavior_feature_list, item_input_layer_dict, embedding_layer_dict)  # 长度为1 
    # 获取行为序列(doc_id序列, hist_doc_id) 对应的embedding，这里有可能有多个行为产生了行为序列，所以需要使用列表将其放在一起
    keys_embed_list = embedding_lookup([varlen_feature_columns[0].name], user_input_layer_dict, embedding_layer_dict)  # 长度为1
    
    # 用户离散特征的输入层与embedding层拼接
    dnn_input_emb_list = embedding_lookup([col.name for col in sparse_feature_columns], user_input_layer_dict, embedding_layer_dict)
    
    # 获取dense
    dnn_dense_input = []
    for fc in dense_feature_columns:
        if fc.name != 'hist_len':  # 连续特征不要这个
            dnn_dense_input.append(user_input_layer_dict[fc.name])
    
    # 把keys_emb_list和query_emb_listpooling操作， 这是因为可能每个商品不仅有id，还可能用类别，品牌等多个embedding向量，这种需要pooling成一个
    history_emb = PoolingLayer()(NoMask()(keys_embed_list))  # (None, 50, 8)
    target_emb = PoolingLayer()(NoMask()(query_embed_list))   # (None, 1, 8)
    
    hist_len = user_input_layer_dict['hist_len']
    # 胶囊网络
    # (None, 2, 8) 得到了两个兴趣胶囊
    high_capsule = CapsuleLayer(input_units=item_embedding_dim, out_units=item_embedding_dim,
                                max_len=seq_max_len, k_max=k_max)((history_emb, hist_len))
    
    
    # 把用户的其他特征拼接到胶囊网络上来
    if len(dnn_input_emb_list) > 0 or len(dnn_dense_input) > 0:
        user_other_feature = combined_dnn_input(dnn_input_emb_list, dnn_dense_input)
        # (None, 2, 32)   这里会发现其他的用户特征是每个胶囊复制了一份，然后拼接起来
        other_feature_tile = tf.keras.layers.Lambda(tile_user_otherfeat, arguments={'k_max': k_max})(user_other_feature) 
        user_deep_input = Concatenate()([NoMask()(other_feature_tile), high_capsule]) # (None, 2, 40)
    else:
        user_deep_input = high_capsule
        
    # 接下来过一个DNN层，获取最终的用户表示向量 如果是三维输入， 那么最后一个维度与w相乘，所以这里如果不自己写，可以用Dense层的列表也可以
    user_embeddings = DNN(user_dnn_hidden_units, dnn_activation, l2_reg_dnn,
                          dnn_dropout, dnn_use_bn, output_activation=output_activation, seed=seed,
                          name="user_embedding")(user_deep_input)  # (None, 2, 8)
    
    # 接下来，过Label-aware layer
    if dynamic_k:
        user_embedding_final = LabelAwareAttention(k_max=k_max, pow_p=p,)((user_embeddings, target_emb, hist_len))
    else:
        user_embedding_final = LabelAwareAttention(k_max=k_max, pow_p=p,)((user_embeddings, target_emb))
    
    # 接下来
    item_embedding_matrix = embedding_layer_dict[item_feature_name]  # 获取doc_id的embedding层
    item_index = EmbeddingIndex(list(range(item_vocabulary_size)))(item_input_layer_dict[item_feature_name]) # 所有doc_id的索引
    item_embedding_weight = NoMask()(item_embedding_matrix(item_index))  # 拿到所有item的embedding
    pooling_item_embedding_weight = PoolingLayer()([item_embedding_weight])  # 这里依然是当可能不止item_id，或许还有brand_id, cat_id等，需要池化
    
    # 这里传入的是整个doc_id的embedding， user_embedding, 以及用户点击的doc_id，然后去进行负采样计算损失操作
    output = SampledSoftmaxLayer(num_sampled)([pooling_item_embedding_weight, user_embedding_final, item_input_layer_dict[item_feature_name]])
    
    model = Model(inputs=user_input_layers+item_input_layers, outputs=output)
    
    # 下面是等模型训练完了之后，获取用户和item的embedding
    model.__setattr__("user_input", user_input_layers)
    model.__setattr__("user_embedding", user_embeddings)
    model.__setattr__("item_input", item_input_layers)
    model.__setattr__("item_embedding", get_item_embedding(pooling_item_embedding_weight, item_input_layer_dict[item_feature_name]))
    
    return model

简单说下流程， 函数式API搭建模型的方式，首先我们需要传入封装好的用户特征描述以及item特征描述，比如：

# 建立模型
user_feature_columns = [
        SparseFeat('user_id', feature_max_idx['user_id'], embedding_dim),
        VarLenSparseFeat(SparseFeat('hist_doc_ids', feature_max_idx['article_id'], embedding_dim,
                                                        embedding_name="click_doc_id"), his_seq_maxlen, 'mean', 'hist_len'),    
        DenseFeat('hist_len', 1),
        SparseFeat('u_city', feature_max_idx['city'], embedding_dim),
        SparseFeat('u_age', feature_max_idx['age'], embedding_dim),
        SparseFeat('u_gender', feature_max_idx['gender'], embedding_dim),
    ]
doc_feature_columns = [
    SparseFeat('click_doc_id', feature_max_idx['article_id'], embedding_dim)
    # 这里后面也可以把文章的类别画像特征加入
]

首先， 函数会对传入的这种特征建立模型的Input层，主要是build_input_layers函数。建立完了之后，获取到Input层列表，这个是为了最终定义模型用的，keras要求定义模型的时候是列表的形式。

接下来是选出sparse特征和Dense特征来，这个也是常规操作了，因为不同的特征后面处理方式不一样，对于sparse特征，后面要接embedding层，Dense特征的话，直接可以拼接起来。这就是筛选特征的3行代码。

接下来，是为所有的离散特征建立embedding层，通过函数build_embedding_layers。建立完了之后，把item相关的embedding层与对应的Input层接起来，作为query_embed_list， 而用户历史行为序列的embedding层与Input层接起来作为keys_embed_list，这两个有单独的用户。而Input层与embedding层拼接是通过embedding_lookup函数完成的。 这样完成了之后，就能通过Input层-embedding层拿到item的系列embedding，以及历史序列里面item系列embedding，之所以这里是系列embedding，是有可能不止item_id这一个特征，还可能有品牌id, 类别id等好几个，所以接下来把系列embedding通过pooling操作，得到最终表示item的向量。 就是这两行代码：

# 把keys_emb_list和query_emb_listpooling操作， 这是因为可能每个商品不仅有id，还可能用类别，品牌等多个embedding向量，这种需要pooling成一个
history_emb = PoolingLayer()(NoMask()(keys_embed_list))  # (None, 50, 8)
target_emb = PoolingLayer()(NoMask()(query_embed_list))   # (None, 1, 8)

而像其他的输入类别特征， 依然是Input层与embedding层拼起来，留着后面用，这个存到了dnn_input_emb_list中。 而dense特征， 不需要embedding层，直接通过Input层获取到，然后存到列表里面，留着后面用。

上面得到的history_emb，就是用户的历史行为序列，这个东西接下来要过兴趣提取层，去学习用户的多兴趣，当然这里还需要传入行为序列的真实长度。因为每个用户行为序列不一样长，通过mask让其等长了，但是真实在胶囊网络计算的时候，这些填充的序列是要被mask掉的。所以必须要知道真实长度。

# 胶囊网络
# (None, 2, 8) 得到了两个兴趣胶囊
high_capsule = CapsuleLayer(input_units=item_embedding_dim, out_units=item_embedding_dim,max_len=seq_max_len, k_max=k_max)((history_emb, hist_len))

通过这步操作，就得到了两个兴趣胶囊。 至于具体细节，下一节看。 然后把用户的其他特征拼接上来，这里有必要看下代码究竟是怎么拼接的：

# 把用户的其他特征拼接到胶囊网络上来
if len(dnn_input_emb_list) > 0 or len(dnn_dense_input) > 0:
    user_other_feature = combined_dnn_input(dnn_input_emb_list, dnn_dense_input)
    # (None, 2, 32)   这里会发现其他的用户特征是每个胶囊复制了一份，然后拼接起来
    other_feature_tile = tf.keras.layers.Lambda(tile_user_otherfeat, arguments={'k_max': k_max})(user_other_feature) 
    user_deep_input = Concatenate()([NoMask()(other_feature_tile), high_capsule]) # (None, 2, 40)
else:
    user_deep_input = high_capsule

这里会发现，使用了一个Lambda层，这个东西的作用呢，其实是将用户的其他特征在胶囊个数的维度上复制了一份，再拼接，这就相当于在每个胶囊的后面都拼接上了用户的基础特征。这样得到的维度就成了(None, 2, 40)，2是胶囊个数， 40是兴趣胶囊的维度+其他基础特征维度总和。这样拼完了之后，接下来过全连接层

# 接下来过一个DNN层，获取最终的用户表示向量 如果是三维输入， 那么最后一个维度与w相乘，所以这里如果不自己写，可以用Dense层的列表也可以
user_embeddings = DNN(user_dnn_hidden_units, dnn_activation, l2_reg_dnn,
                          dnn_dropout, dnn_use_bn, output_activation=output_activation, seed=seed,
                          name="user_embedding")(user_deep_input)  # (None, 2, 8)

最终得到的是(None, 2, 8)的向量，这样就解决了之前的那个疑问， 最终得到的兴趣向量个数并不是1个，而是多个兴趣向量了，因为上面用户特征拼接，是每个胶囊后面都拼接一份同样的特征。另外，就是原来DNN这里的输入还可以是3维的，这样进行运算的话，是最后一个维度与W进行运算，相当于只在第3个维度上进行了降维操作后者非线性操作，这样得到的兴趣个数是不变的。

这样，有了两个兴趣的输出之后，接下来，就是过LabelAwareAttention层了，对这两个兴趣向量与当前item的相关性加注意力权重，最后变成1个用户的最终向量。

user_embedding_final = LabelAwareAttention(k_max=k_max, pow_p=p,)((user_embeddings, target_emb))

这样，就得到了用户的最终表示向量，当然这个操作仅是训练的时候，服务的时候是拿的上面DNN的输出，即多个兴趣，这里注意一下。

拿到了最终的用户向量，如何计算损失呢？ 这里用了负采样层进行操作，之前，在YouTubeDNN的时候，其实并没有留意到这个细节操作。当时只是跑通了，而这次借着复现MIND，终于看到了这个负采样操作真实情况是如何操作的。

这里要好好说下我的理解，首先我先把这几行代码拿过来：

item_embedding_matrix = embedding_layer_dict[item_feature_name]  # 获取doc_id的embedding层
item_index = EmbeddingIndex(list(range(item_vocabulary_size)))(item_input_layer_dict[item_feature_name]) # 所有doc_id的索引
item_embedding_weight = NoMask()(item_embedding_matrix(item_index))  # 拿到所有item的embedding
pooling_item_embedding_weight = PoolingLayer()([item_embedding_weight])  # 这里依然是当可能不止item_id，或许还有brand_id, cat_id等，需要池化
    
# 这里传入的是整个doc_id的embedding， user_embedding, 以及用户点击的doc_id，然后去进行负采样计算损失操作
output = SampledSoftmaxLayer(num_sampled)([pooling_item_embedding_weight, user_embedding_final, item_input_layer_dict[item_feature_name]])
    
model = Model(inputs=user_input_layers+item_input_layers, outputs=output)

拿到用户的embedding之后，接下来，开始获取item在embedding层的embedding矩阵，即拿出了所有item对应的embedding，这个embedding当然也是pooling之后的，用pooling_item_embedding_weight表示。 有了所有item的embedding矩阵，有了user_embedding，又有当前用户产生行为的item的索引，那么过一个SampledSoftmaxLayer层就能求得损失。这个层有必要先看下：

class SampledSoftmaxLayer(Layer):
    def __init__(self, num_sampled=5, **kwargs):
        self.num_sampled = num_sampled
        super(SampledSoftmaxLayer, self).__init__(**kwargs)
    def build(self, input_shape):
        self.size = input_shape[0][0]   # docs num
        self.zero_bias = self.add_weight(shape=[self.size], initializer=Zeros, dtype=tf.float32, trainable=False, name='bias')
        super(SampledSoftmaxLayer, self).build(input_shape)
    def call(self, inputs_with_label_idx):
        embeddings, inputs, label_idx = inputs_with_label_idx
        # 这里盲猜下这个操作，应该是有了label_idx，就能拿到其embedding，这个是用户行为过多
        # 所以(user_embedding, embedding[label_idx])就是正样本
        # 然后根据num_sampled，再从传入的embeddings字典里面随机取num_sampled个负样本
        # 根据公式log(sigmoid(user_embedding, embedding[label_idx])) + 求和(log(sigmoid(-user_embedding, embedding[负样本])))得到损失
        loss = tf.nn.sampled_softmax_loss(weights=embeddings,   # (numclass, dim)
                                          biases=self.zero_bias,  # (numclass)
                                          labels=label_idx,   # (batch, num_true)
                                          inputs=inputs,  # (batch, dim)
                                          num_sampled=self.num_sampled, # 负采样个数
                                          num_classes=self.size  # 类别数量
                                         )
        return tf.expand_dims(loss, axis=1)

这里其实计算损失的时候使用的tf.nn.sampled_softmax_loss函数，参数主要有这么几个：

• weights: 这个是所有item的embedding矩阵
• labels: 当前交互的item在矩阵里面的索引，通过这个就能拿到对应的embedding，这个是正样本
• inputs: 用户embedding
• num_sampled: 负采样个数

有这几个，我这里就盲猜了下这个负采样loss究竟是咋计算的，当然底层我没看过啊，凭感觉来的，所以如果理解错了的话，欢迎在评论区交流呀。

首先，在学习w2v的时候，负采样的目标是这么定义的：
$$\log \sigma \left(v_{w_O}^{\prime }{}^{\top }{v}_{w_I}\right)+\sum _{i=1}^k{\mathbb{E}}_{w_i\sim P_n(w)}\left[\log \sigma \left(-v_{w_i}^{\prime }{}^{\top }{v}_{w_I}\right)\right]$$
我们就是希望公式里面的$v_{wI}$与$v_{wo}$离得尽量近，而与后面负采样的k个$v_{wi}$负样本离得尽量远。 这里其实也是同理， 我们的用户embedding就相当于$v_{wI}$， 而当前交互的item的embedding就相当于$v_{wo}$，而有了item的embedding矩阵，又有了num_sampled，那么这个函数当然可以随机从embedding矩阵中采样num_sampled个负样本向量，作为$v_{wi}$，于是乎，loss就产生了。

到了这里，我有意识到一个问题，不是在产生样本的时候，事先做过负样本采样嘛， 那时候已经有负样本了呀，也就是label为0的样本。 对于这样的样本，我传进来怎么办？ 模型不就误认为当前的行为item也与用户相关了吗，此时不就学错了？ 带着这个问题，我又去看了YouTubeDNN那里生成数据集的源码， 就会发现是这么写的：

def gen_data_set(data, negsample=0):
    data.sort_values("timestamp", inplace=True)
    item_ids = data['movie_id'].unique()
    train_set = []
    test_set = []
    for reviewerID, hist in tqdm(data.groupby('user_id')):
        pos_list = hist['movie_id'].tolist()
        rating_list = hist['rating'].tolist()
        if negsample > 0:
            candidate_set = list(set(item_ids) - set(pos_list))
            neg_list = np.random.choice(candidate_set,size=len(pos_list)*negsample,replace=True)
        for i in range(1, len(pos_list)):
            hist = pos_list[:i]
            if i != len(pos_list) - 1:
                train_set.append((reviewerID, hist[::-1], pos_list[i], 1, len(hist[::-1]),rating_list[i]))
                for negi in range(negsample):
                    train_set.append((reviewerID, hist[::-1], neg_list[i*negsample+negi], 0,len(hist[::-1])))
            else:
                test_set.append((reviewerID, hist[::-1], pos_list[i],1,len(hist[::-1]),rating_list[i]))
    random.shuffle(train_set)
    random.shuffle(test_set)
    return train_set,test_set

这里有没有发现negsample=0。也就是默认是不进行负采样操作的，这样，就相当于训练集里全是正样本，label为1。 而真正计算损失的时候，对于正样本随机采负样本进行计算把模型训练收敛，这样才真正的合理。 所以我觉得如果这里使用sampled_softmax_loss， 那么一开始数据集里就不要有负样本， 如果一开始数据集里就进行了采样，那么这里就用普通的二分类交叉熵损失即可，而不要用sampled_softmax_loss。

之前的YouTubeDNN那里，没有注意到这个问题，这里特地注意了下，这个我在MIND这里实验过， 如果生成样本的时候， negsample=0, 召回评估的效果会好很多。

接下来有几行代码也需要注意：

# 下面是等模型训练完了之后，获取用户和item的embedding
model.__setattr__("user_input", user_input_layers)
model.__setattr__("user_embedding", user_embeddings)
model.__setattr__("item_input", item_input_layers)
model.__setattr__("item_embedding", get_item_embedding(pooling_item_embedding_weight, item_input_layer_dict[item_feature_name]))

这几行代码是为了模型训练完，我们给定输入之后，拿embedding用的，设置好了之后，通过：

user_embedding_model = Model(inputs=model.user_input, outputs=model.user_embedding)
item_embedding_model = Model(inputs=model.item_input, outputs=model.item_embedding)

user_embs = user_embedding_model.predict(test_user_model_input, batch_size=2 ** 12)
# user_embs = user_embs[:, i, :]  # i in [0,k_max) if MIND
item_embs = item_embedding_model.predict(all_item_model_input, batch_size=2 ** 12)

这样就能拿到用户和item的embedding， 接下来近邻检索完成召回过程。 注意，MIND的话，这里是拿到的多个兴趣向量的。

到这里， MIND模型的代码宏观，我们就过完了，收获蛮大的这次。下面看下这篇paper里面提出的两个创新点的代码细节。

5.2 多兴趣提取层

多兴趣提取层是这篇paper的核心，原理从上面讲了， 这里直接上代码：

class CapsuleLayer(Layer):
    def __init__(self, input_units, out_units, max_len, k_max, iteration_times=3, init_std=1.0, **kwargs):
        self.input_units = input_units
        self.out_units = out_units
        self.max_len = max_len
        self.k_max = k_max
        self.iteration_times = iteration_times
        self.init_std = init_std
        super(CapsuleLayer, self).__init__(**kwargs)
    
    def build(self, input_shape):
        # 路由对数，大小是1，2，50， 即每个路由对数与输入胶囊个数一一对应，同时如果有两组输出胶囊的话， 那么这里就需要2组B
        self.routing_logits = self.add_weight(shape=[1, self.k_max, self.max_len],
                                             initializer=RandomNormal(stddev=self.init_std),
                                             trainable=False, name='B', dtype=tf.float32)
        # 双线性映射矩阵，维度是[输入胶囊维度，输出胶囊维度] 这样才能进行映射
        self.bilinear_mapping_matrix = self.add_weight(shape=[self.input_units, self.out_units],
                                                       initializer=RandomNormal(stddev=self.init_std),
                                                       name="S", dtype=tf.float32)
        super(CapsuleLayer, self).build(input_shape)
    
    def call(self, inputs, **kwargs):
        # input (hist_emb, hist_len) ,其中hist_emb是(None, seq_len, emb_dim), hist_len是(none, 1) batch and sel_len
        behavior_embeddings, seq_len = inputs
        batch_size = tf.shape(behavior_embeddings)[0]
        seq_len_tile = tf.tile(seq_len, [1, self.k_max])  # 在第二个维度上复制一份 k_max个输出胶囊嘛 (None, 2)  第一列和第二列都是序列真实长度
        
        for i in range(self.iteration_times):
            mask = tf.sequence_mask(seq_len_tile, self.max_len)  #（None, 2, 50) 第一个维度是样本，第二个维度是胶囊，第三个维度是[True, True, ..False, False, ..]
            pad = tf.ones_like(mask, dtype=tf.float32) * (-2**32+1) # (None, 2, 50)  被mask的位置是非常小的数，这样softmax的时候这个位置正好是0
            routing_logits_with_padding = tf.where(mask, tf.tile(self.routing_logits, [batch_size, 1, 1]), pad) 
            # (None, 2, 50) 沿着batch_size进行复制，每个样本都得有这样一套B，2个输出胶囊， 50个输入胶囊

            weight = tf.nn.softmax(routing_logits_with_padding) # (none, 2, 50)  # softmax得到权重
    
            # (None, seq_len, emb_dim) * (emb_dim, out_emb) = (None, 50, 8) axes=1表示a的最后1个维度，与b进行张量乘法
            behavior_embedding_mapping = tf.tensordot(behavior_embeddings, self.bilinear_mapping_matrix, axes=1)
            
            Z = tf.matmul(weight, behavior_embedding_mapping) # (None, 2, 8)即 上面的B与behavior_embed_map加权求和
            interest_capsules = squash(Z) # (None, 2, 8) 
            
            delta_routing_logits = tf.reduce_sum(
                # (None, 2, 8)  * (None, 8, 50) = (None, 2, 50)
                tf.matmul(interest_capsules, tf.transpose(behavior_embedding_mapping, perm=[0, 2, 1])),
                axis=0, keep_dims=True
            ) # (1, 2, 50)   样本维度这里相加  所有样本一块为聚类做贡献

            self.routing_logits.assign_add(delta_routing_logits)  # 原来的基础上加上这个东西 （1, 2, 50)
        
        interest_capsules = tf.reshape(interest_capsules, [-1, self.k_max, self.out_units])  # (None, 2, 8)
        return interest_capsules

本质上，这就是胶囊网络动态路由机制的计算，每一步我都注释了出来，需要留意的点第一个是，多个输出胶囊这里可以用矩阵进行一步到位计算。 另外一个就是更新对数路由的时候，是要加上之前的路由对数的，论文公式里面，貌似是没有加。这里和胶囊网络计算保持了一致。

5.3 label-Aware Attention

这个层本质上就是实现了一个注意力机制，这里面的聚类个数k实现了动态调整的可以看下是怎么实现的那个公式：

class LabelAwareAttention(Layer):
    def __init__(self, k_max, pow_p=1, **kwargs):
        self.k_max = k_max
        self.pow_p = pow_p
        super(LabelAwareAttention, self).__init__(**kwargs)
    def build(self, input_shape):
        self.embedding_size = input_shape[0][-1]
        super(LabelAwareAttention, self).build(input_shape)
    def call(self, inputs):
        keys, query = inputs[0], inputs[1]  # keys (None, 2, 8)  query (None, 1, 8)
        weight = reduce_sum(keys * query, axis=-1, keep_dims=True)  # (None, 2, 1)
        weight = tf.pow(weight, self.pow_p)  # (None, 2, 1)
        
        # k如果需要动态调整，那么这里就根据实际长度mask操作，这样被mask的输出胶囊的权重为0， 发挥不出作用了
        if len(inputs) == 3:
            k_user = tf.cast(tf.maximum(
                1.,
                tf.minimum(
                    tf.cast(self.k_max, dtype="float32"),  # k_max
                    tf.log1p(tf.cast(inputs[2], dtype="float32")) / tf.log(2.)  # hist_len
                )
            ), dtype="int64")
            seq_mask = tf.transpose(tf.sequence_mask(k_user, self.k_max), [0, 2, 1])
            padding = tf.ones_like(seq_mask, dtype=tf.float32) * (-2 ** 32 + 1)  # [x,k_max,1]
            weight = tf.where(seq_mask, weight, padding)
        
        weight = softmax(weight, dim=1, name='weight')
        output = reduce_sum(keys * weight, axis=1)  # (None, 8)
        return output

别的这里就没有啥好说的了。

PS： MIND模型的代码剖析就到这里，另外声明下，我上面的建议模型代码只是为了学习和简单理解模型的运行原理使用，如果真正想用MIND跑任务的话，建议用deepmatch包里面实现的模型。目的上不一样，我这里简易版本是为了搞清楚模型代码细节，而deepmatch我觉得代码可读性和易懂性上不强，对新手有些不友好，但是人家功能齐全，有很多容错机制以及异常处理，模型加速等技术，并且模型能进行保存，我这里由于自定义层里面省去了一些必要配置，所以模型也无法保存。 所以不适合真实任务中使用，我也没必要再重复造轮子哈哈。 之所以这么强调，是因为之前又伙伴私聊我关于模型代码方面的问题，涉及到了模型保存，效果以及简单改东西报错啥的，所以我得在这里解释下。这里的简易版本，只够去了解模型原理的，不能在实际任务中使用。

跑deepmatch的MIND模型也非常简单，后面我GitHub里面给出了参考，当时我尝试直接从YouTubeDNN那个代码上改成MIND来跑，因为我发现deepmatch给的例子就是那样，但是在我这里报错了，原因是起的名字符合要求。如果要跑人家的MIND模型，这里必须改成：

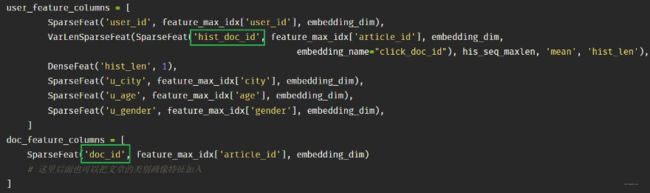
这俩名字必须只差个"hist_"才行，因为MIND模型源代码里面会通过hist_去找用户历史行为特征列，如果不是这样定义，会报错找不到这个。 其他的就和YouTubeDNN的一样了。

我把简易版本以及Deepmatch版本的MIND代码都上传到了GitHub，感兴趣的可以在那里看啦。

6. 小总

今天这篇文章整理的MIND，这是一个多兴趣的召回模型，核心是兴趣提取层，该层通过动态路由机制能够自动的对用户的历史行为序列进行聚类，得到多个兴趣向量，这样能在召回阶段捕获到用户的广泛兴趣，从而召回更好的候选商品。 另外一个点就是LabelAwareAttention， 不过这个并不是什么太新颖的地方，普通的Attention机制了。胶囊网络的思路还是挺有意思的，当然胶囊网络和动态路由机制还可以用在其他类似于聚类或者产生可解释性向量的地方。 那么有没有想过一个问题呀，为啥这个地方用传统的聚类方法就不行呢？ 比如Kmeans这种，我的理解是之所以不太适用，可能有两个原因，第一个可能是这种传统的聚类方法，没法做到泛化，比如就拿Kmeans来说，如果拿到用户的历史行为序列进行聚类的话，首先这个序列长短不一，直接聚类效果肯定不会很好，并且每次都进行聚类的话非常费时，如果想让它work，那么我能想到的就是先把所有商品进行聚类，这样在拿到每个用户行为序列的时候，看看是分别数据哪些类别，这样每个类别的向量进行pooling得到用户兴趣向量，但对所有商品先进行聚类这样也不太现实或者太复杂。另外一个就是即使聚完类了，当用户再有新行为发生时，就又需要重新计算兴趣向量，这个实时性上太花费时间。还有就是聚完类，对每个行为序列都得先看看分别属于哪个类，再pooling感觉也花费不少时间。所以传统聚类算法对这个场景是不行的。那么胶囊网络怎么就行了呢？ 我理解，这个模型训练的时候通过调整参数进行聚类，首先是有泛化性的，不同的行为序列都对参数调整有帮助，所以可以边喂数据边通过聚类调整参数。其次，只要模型一旦训练好，再有新行为，无非就是多了个行为胶囊而已，通过动态路由计算，是能训练的更新兴趣胶囊向量的，实时性上也有一定帮助。当然，这些都是自己的一点想法了，欢迎讨论呀。

这篇文章从看论文，到代码复现，到整理出来大约花费了两天半的时间，当然这个由于涉及到胶囊网络的知识，特地找其他视频看了下，不过，整体下来也是有一些收获吧，之前一直想看胶囊网络的，这次要不是和伙伴们互相分享知识，估计还一直拖着，但突击完之后发现，其实也没有那么难，看来就是比较懒而已哈哈。

这段时间好几条线走着，毕设，cv，机器学习，再加上推荐模型，其实还是有点忙的，后面推荐这块的话，打算当做业余爱好进行更了，主流的一些关键模型也差不多了，排序那块还有多任务没有涉及，召回的话还有双塔系列，这些争取在毕业之前搞定。更新频率的话，大致上一到两周一个吧，有了这些基础模型和思想做铺垫，我想伙伴们能更快的入门推荐系统啦，加油

参考：

• Multi-Interest Network with Dynamic Routing for Recommendation at Tmall
• Dynamic Routing Between Capsule
• CIKM2019｜MIND—召回阶段的多兴趣模型
• B站胶囊网络课程
• 胶囊网络识别交通标志

整理这篇文章的同时， 也建立了一个GitHub项目， 准备后面把各种主流的推荐模型用复现一遍，并用通俗易懂的语言进行注释和逻辑整理， 今天的MIND模型代码已经上传， 该GitHub项目只是单纯供学习使用， 不作任何商业用途，感兴趣的可以看一下 ，star下我会更开心哈哈

筋斗云：https://github.com/zhongqiangwu960812/AI-RecommenderSystem