机器学习 KD树_递归搜索(matlab实现)

思路

KD书基本思路：
建立KD树(Kd_Tree_Create)
递归搜索：回溯搜索的起点(Kd_Tree_Search)
回溯搜索：收敛到全局最近点(暂未实现)

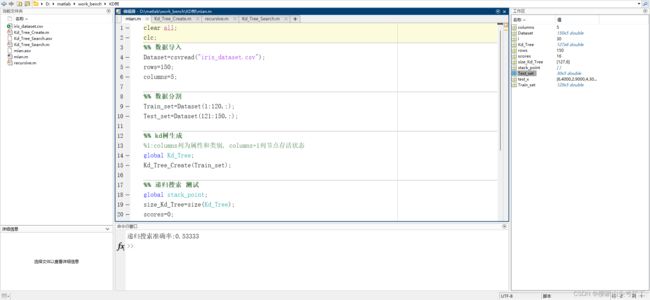
效果

仅用递归搜索效果如下：

代码

mian

clear all;
clc;
%% 数据导入
Dataset=csvread("iris_dataset.csv");
rows=150;
columns=5;

%% 数据分割
Train_set=Dataset(1:120,:);
Test_set=Dataset(121:150,:);

%% kd树生成
%1:columns列为属性和类别, columns+1列节点存活状态
global Kd_Tree;
Kd_Tree_Create(Train_set);

%% 递归搜索 测试
global stack_point;
size_Kd_Tree=size(Kd_Tree);
scores=0;
for i=1:30
    test_x=Test_set(i,1:columns-1);
    Kd_Tree_Search(1,size_Kd_Tree(1),columns-1,1,test_x);
    if (Kd_Tree(stack_point(1),columns)==Test_set(i,columns))
        scores=scores+1;
    end
    stack_point=[];
end
disp("递归搜索准确率:"+scores/30);

%% 递归 & 回溯搜索 测试

Kd_Tree_Create

function [] = Kd_Tree_Create(Dataset)
%二叉树数据结构在c语言中容易表示,可在matlab中却不那么容易
%但是c语言需要自己造轮子(sortrows()用c得写死我), matlab有现成的, 所以思考一下如何在matlab中表示二叉树呢
%参考大堆小堆利用数组表示二叉树, 从而避开指针构建kdtree(哇噢, 感觉自己就是个小机灵鬼诶)
%给每个节点添加下标以实现父子访问
%提示:节点下标为i, 左孩子下标为2*i,左孩子下标为2*i+1
%因为kdtree不是完全二叉树, 所以需要增加状态信息栏表示某节点是否为空
%好了, 开整吧

%Dataset共有rows行数据,1:columns-1列为属性,columns列为类别
size_Dataset=size(Dataset);
recursive(Dataset,1,1,size_Dataset(1),size_Dataset(2)-1);
end

recursive

function [] = recursive(Dataset,pos,x_i,rows,columns)
%Dataset:需要二分的数据集
%rows:需分类的个体数
%columns:用于分类的属性数
%pos:Kd_Tree插入位置
%x_i:排序依据
global Kd_Tree;
if(rows>1)
    %排序
    Dataset=sortrows(Dataset,mod(x_i-1,columns)+1);
    %二分
    Divi_Index=fix(rows/2);
    Kd_Tree(pos,1:columns+1)=Dataset(Divi_Index+1,:);
    Kd_Tree(pos,columns+2)=1;
    %递归
    recursive(Dataset(1:Divi_Index,:),2*pos,x_i+1,Divi_Index,columns);
    recursive(Dataset(Divi_Index+2:rows,:),2*pos+1,x_i+1,rows-Divi_Index-1,columns);
else
    if(rows==1)
        Kd_Tree(pos,1:columns+1)=Dataset;
        Kd_Tree(pos,columns+2)=1;
    else
        Kd_Tree(pos,columns+2)=0;
    end
end

end

Kd_Tree_Search

function [] = Kd_Tree_Search(current_point,rows,x_dim,i_x,test_x)
global Kd_Tree;
global stack_point;
stack_point=[current_point stack_point];
if(Kd_Tree(current_point,i_x)<=test_x(1,i_x))%进入右子节点
    if(2*current_point+1<=rows && Kd_Tree(2*current_point+1,x_dim+2)==1)
        Kd_Tree_Search(2*current_point+1,rows,x_dim,mod(i_x-1,x_dim)+1,test_x)
    else%父与右子之间 && 右子为空
    end
else%进入左子节点
    if(2*current_point<=rows && Kd_Tree(2*current_point,x_dim+2)==1)
        Kd_Tree_Search(2*current_point,rows,x_dim,mod(i_x-1,x_dim)+1,test_x)
    else%父与左子之间 && 左子为空
    end
end


end