机器学习笔记（二）1

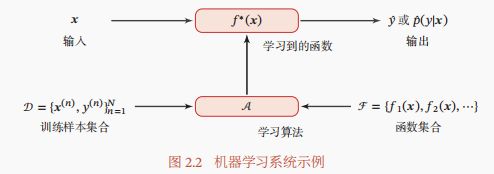
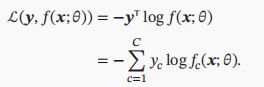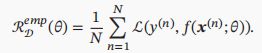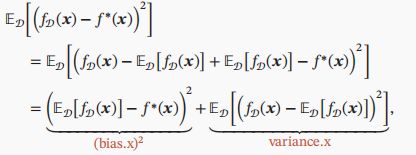　　1.机器学习（通过数据来学习）

　　机器学习（Machine Learning，ML）就是让计算机从数据中进行自动学习，得到某种知识（或规律）。

　　早期又叫模式识别PR（偏向具体任务，eg：光学字符识别、语音识别、人脸识别等）

　　2.基本概念

特征/属性：

标签：：=>样本/示例

数据集/语料库

训练集/测试样本

测试集/训练样本

特征向量

　　

 

 

 　　　　　　　　　　　　学习算法A又叫学习器

　　3.三要素

1.模型：

　　根据经验来假设一个函数集合ℱ，称为假设空间（Hypothesis Space），然后通过观测其在训练集 上的特性，从中选择一个理想的假设（Hypothesis）∗ ∈ ℱ．

　　假设空间ℱ 通常为一个参数化的函数族ℱ = {(; )| ∈ ℝ},其中(; )是参数为 的函数，也称为模型（Model）， 为参数的数量． 

　　

　　线性模型：（权重w 偏置b）
　　非线性模型：其中() = [1 (), 2 (), ⋯ , ()]T为 个非线性基函数组成的向量，参数 包含了权重向量和偏置．如果()本身为可学习的基函数

，比如 其中 ℎ(⋅) 为非线性函数，′ () 为另一组基函数， 和 为可学习的参数，则(; )就等价于神经网络模型．

 

2.学习准则：

　　一个好的模型(, ∗) 应该在所有 (, ) 的可能取值上都与真实映射函数 = ()一致，即|(, ∗ ) − | < , ∀(, ) ∈ × ,或与真实条件概率分布 (|)一致，即| (, ∗ ) − (|)| < , ∀(, ) ∈ × ,其中是一个很小的正数， (, ∗)为模型预测的条件概率分布中对应的概率．模型(; )的好坏可以通过期望风险(Expected Risk）ℛ()来衡量，其定义为ℛ() = (,)∼ (,)[ℒ(, (; ))],其中 (, )为真实的数据分布，ℒ(, (; ))为损失函数，用来量化两个变量之间的差异．

　　1.损失函数：（量化模型预测和真实标签之间的差异）

　　　　　　0-1损失函数：不连续且导数为0，难以优化．因此经常用连续可微的损失函数替代

　　　　　　平方损失函数：不适用于分类问题　

 

 

 

 

　　　　　　交叉熵损失函数：适用于分类问题，用one-hot向量y表示样本标签，类别为k

　　　　　　　　　　=====>

 

　　　　　　Hinge损失函数：eg：二分类中

 

 

　　2.风险最小化准则 　　

　　由于不知道真实的数据分布和映射函数，实际上无法计算其期望风险ℛ()．但可以计算的是经验风险（训练集上的平均损失）

找参数使其最小，，（经验风险最小化ERM）

 

 　　过拟合：ERM+参数正则化（多采用L2，L1使得参数稀疏性）

　　欠拟合

 

 

3.优化算法：

　　参数：通过优化算法可学习的θ　　　　　　超参数：定义模型结构或优化策略，分类k，梯度步长，神经网络层数

　　1.梯度下降法

　　2.提前停止

　　3.随机梯度下降法

　　4.小批量梯度下降法

 

　　4.简单示例：线性回归

　　增广权重向量w （+1），增广特征向量b（+b）

最优化要参数估计：经验风险最小化：（最小二乘法：逆矩阵+满秩，不可逆要先主成分，在最小二乘再使用梯度下降【最小均方LMS算法】）

　　　　　　　　　结构风险最小化：岭回归，给 T 的对角线元素都加上一个常数使得( T+ )满秩，即其行列式不为0

　　　　　　　　　最大似然估计：使对数似然函数最大（结果同最小二乘法）

　　　　　　　　　最大后验估计：贝叶斯估计，参数加先验。最大后验估计MAP是指最优参数为后验分布(|, ; , )中概率密度最高的参数。无信息先验，则退化为最大似然估计。

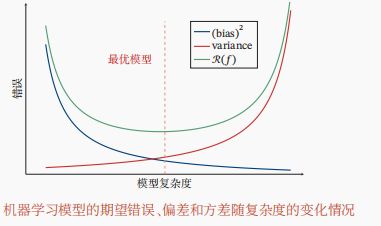
　　5.偏差-方差分解　　　　

　　　　最小化期望错误等价于最小化偏差和方差之和．variance方差一般会随着训练样本的增加而减少。

　　　　

　　随着模型复杂度的增加，模型的拟合能力变强，偏差减少而方差增大，从而导致过拟合．以结构风险最小化为例，我们可以调整正则化系数 来控制模型的复杂度．当 变大时，模型复杂度会降低，可以有效地减少方差，避免过拟合，但偏差会上升．当 过大时，总的期望错误反而会上升。

　　　　　　

　　还有一种有效降低方差的方法为集成模型，即通过多个高方差模型的平均来降低方差． 

 

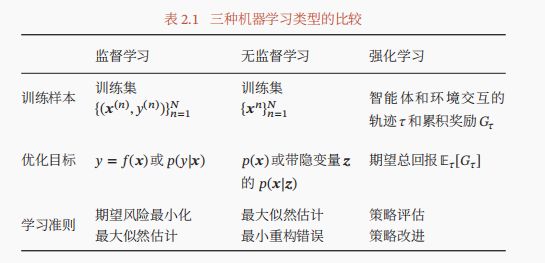
 　　6.算法类型

　　监督学习：分类、回归、结构化学习
　　无监督学习：聚类、密度估计、特征学习、降维
　　强化学习：交互

　　

 

 　　7.特征表示

　　图像特征：向量

　　文本特征：词袋、N元特征词袋

　　如何让机器自动地学习出有效的特征也成为机器学习中的一项重要研究内容，称为特征学习（Feature Learning），也叫表示学习

　　特征学习：选择+抽取