myCobot pro 机械臂（4）正向运动学——改进DH表示法（开发环境：python）

 我只能说，写这篇博客太艰难了……一定要沉住耐心……这个型号的机械臂与官方给的手册里面的参数是有出入的……

感谢《台大机器人学课程》《机器人学之运动学笔记【3】—— 机械臂DH表示法+正向运动学（Forward Kinematics）》以及《机器人工程师进阶之路（二）6轴机械臂D-H法建模》

目录

一、空间中转轴的相对几何关系

1、连杆坐标系

2、DH参数

二、DH参数建立步骤

1、建立模型

（1）确定各关节以及关节轴线Axis i

（2）确定zi轴

（3）确定原点i以及xi轴

（4）添加首尾坐标系

2、确定DH的4个参数

（1）确定αi-1：{大小：zi-1指向zi的角度；符号：右手螺旋定则指向与xi-1相同时为+}

（2）确定ai-1：{大小：zi-1指向zi的距离；符号：沿着xi-1为+，a>0}

（3）确定di：{大小：xi-1指向xi的距离；符号：沿着zi为+，d不一定±}

（4）确定θi：{大小：xi-1指向xi的角度；符号：右手螺旋定则指向与zi相同时为+}

3、offset参数

三、用Python求解正向运动学：计算转换矩阵T

四、回答上文“二/1/（3）”中设置的tips问题）

---

这里对myCobot Pro机械臂采用改进DH表示法描述机械臂，下面将会详细介绍流程：

一、空间中转轴的相对几何关系

一般机械臂初始位置被认为是整体伸直向上。

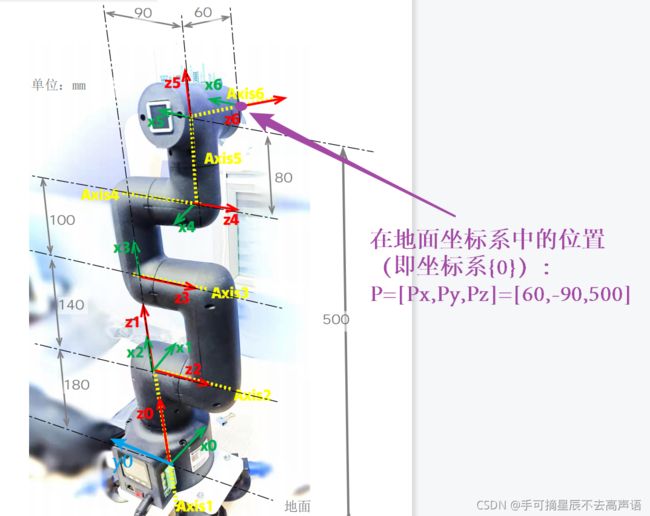
如下图所示：（我这里保持官方给的关节刻度相对准，图中→带+的符号表示电机正转方向）

1、连杆坐标系

2、DH参数

在改进DH法中，描述连杆之间的位置关系，需要用到4个量：（这4个量组成DH参数）

连杆长度a：两个关节的轴（旋转关节的旋转轴，平移关节的平移轴）之间的公共法线长度

连杆扭矩α：一个关节的轴相对于另一个关节的轴绕它们的公共法线旋转的角度

连杆偏距d：一个关节与下一个关节的公共法线和它与上一个关节的公共法线沿这个关节轴的距离

关节转角θ：一个关节与下一个关节的公共法线和它与上一个关节的公共法线绕这个关节轴的转角

连杆长度a、连杆扭矩α、连杆偏距d、关节转角θ（旋转关节，θ为变量；移动关节，d为变量）

 在myCobot当中，全都是Revolute joint关节，因此，4个量中，只有θ是变量

列表如下： 

i	αi-1(alpha_i-1)	ai-1	di	θi	offset
1
2
3
4
5
6

二、DH参数建立步骤

1、建立模型

（1）确定各关节以及关节轴线Axis i

每一个关节轴线确定一个坐标系

（2）确定zi轴

 z轴的位置为当前轴线，方向任意（此处选择电机正转方向，通过右手螺旋定则判断出z轴的正方向），同时z轴的下标表示第几坐标系。

（3）确定原点i以及xi轴

{i}坐标系的原点与xi轴：

        ①（情况存在：{1}、{4}、{5}）Axis i与Axis i+1如果相交，交点为原点，xi的方向在两轴线所在平面的垂线上，通常取为右手螺旋定则（zi指向zi+1）的正方向；

        ②（无需考虑）Axis i与Axis i+1如果不相交，两轴线公垂线和当前关节i轴线的交点为原点，x_i为在公垂线上，方向任意（沿着ai的方向，一般指向后一个关节）；

        ③（情况存在：{2}、{3}）Axis i与Axis i+1如果平行，公垂线有无数条，此时连杆偏距d明显为0，xi在公垂线上，指向Axis i+1，且指向坐标系{i+1}的原点。

需要注意的是，当坐标系{2}的原点定了以后，那么坐标系{3}的原点就在x2的延长线上

tips：这里关于坐标系{2}为什么和{1}重合，我认为是不一定非要用这种方式的（可以不重合），这里先存下一个疑惑，之后会通过计算进行回答！

（4）添加首尾坐标系

在改进DH坐标系中，已经标注好{6}了，所以在首端添加{0}。

为了简化，通常使 {0} 和 {1} 一致，并且当第一个关节变量θ1为0时，{0} 和 {1} 会重合。

2、确定DH的4个参数

“拿出第一步列的表，挨个进行填写。先不要在意参数下角标，因为会混淆。”

首先确定，机械臂的尺寸参数：

在改进DH法中，坐标的变换都是从前面的坐标系往下一个坐标系变换，写第i行时只要关注{i-1}和{i}之间的关系就好。

顺序是：

以下将从坐标系{i}中去考虑。例如，当i=1时，利用{0}的坐标系变换到{1}，此时确定α0，a0，d1，θ1

（1）确定αi-1：{大小：zi-1指向zi的角度；符号：右手螺旋定则指向与xi-1相同时为+}

        先将坐标系{i-1}的zi-1轴绕xi-1轴转到与坐标系{i}的zi轴平行，转过的角度为αi-1，右手准则拇指指向为z正方向为正；

i	αi-1(alpha_i-1)	ai-1	di	θi	offset
1  {0}-{1}	α0（z0-z1）=0

（2）确定ai-1：{大小：zi-1指向zi的距离；符号：沿着xi-1为+，a>0}

        如果两关节轴相交，或者重合，则a=0

i	αi-1(alpha_i-1)	ai-1	di	θi	offset
1  {0}-{1}	α0（z0-z1）=0	a0（z0-z1）=0

（3）确定di：{大小：xi-1指向xi的距离；符号：沿着zi为+，d不一定±}

        如果xi-1与xi平行，那么之间的距离就是di

i	αi-1(alpha_i-1)	ai-1	di	θi	offset
1  {0}-{1}	α0（z0-z1）=0	a0（z0-z1）=0	d1（x0-x1）=180

（4）确定θi：{大小：xi-1指向xi的角度；符号：右手螺旋定则指向与zi相同时为+}

        由于之前——选择电机正转方向，通过右手螺旋定则判断出z轴的正方向，因此这里的θ取得全部是电机转动的方向，正转则为+，反转则为-

i	αi-1(alpha_i-1)	ai-1	di	θi	offset
1  {0}-{1}	α0（z0-z1，x0）=0	a0（z0-z1）=0	d1（x0-x1，z1）=180	θ1（x0-x1）=θ1

因此，改进DH参数表为：

改进DH法参数表

i	αi-1(alpha_i-1)	ai-1	di	θi	offset
1  {0}-{1}	0	0	180	θ1
2  {1}-{2}	90	0	0	θ2
3  {2}-{3}	0	140	0	θ3
4  {3}-{4}	0	100	90	θ4
5  {4}-{5}	90	0	80	θ5
6  {5}-{6}	90	0	60	θ6

3、offset参数

        offset指的是：设置的机械臂的初始姿态与DH描述的数学模型机械臂之间的偏移量，旋转为角度，平移为距离。（我理解的是，offset即与变量有关，这里的mycobot的变量为θ，在这里其实指的就是机械臂初始的θ角度）

        DH描述的数学模型机械臂的姿态的初始情况表示xi-1与x平行

        在旋转关节中，offset=0表示xi-1与x平行

        如果offset=-90，那么表示电机正转转过90度才为回到零初始状态（即初始状态）

故得到完整的改进DH参数表：

i	αi-1(alpha_i-1)	ai-1	di	θi	offset
1  {0}-{1}	0	0	180	θ1	0
2  {1}-{2}	90	0	0	θ2	90
3  {2}-{3}	0	140	0	θ3	0
4  {3}-{4}	0	100	90	θ4	90
5  {4}-{5}	90	0	80	θ5	-90
6  {5}-{6}	90	0	60	θ6	0

三、用Python求解正向运动学：计算转换矩阵T

        两 Link Frame 之间的 Transformations：

通过python代码表示：

def Link_Transformation(last_i,i,a_list,alpha_list,d_list,theta_list):
    """
    function：坐标系{i-1}到坐标系{i}的转换矩阵
    tips：这里的last_i指的是i-1
    """
    i = i  # 下面使用的i-1表示列表的第i-1个数，注意同DH参数里的i-1区别
    T_martix = np.mat(np.zeros((4,4)))
    
    T_martix[0,0] = np.cos(theta_list[i-1])
    T_martix[0,1] = -1*np.sin(theta_list[i-1])
    T_martix[0,2] = 0
    T_martix[0,3] = a_list[i-1]
    
    T_martix[1,0] = np.sin(theta_list[i-1])*np.cos(alpha_list[i-1])
    T_martix[1,1] = np.cos(theta_list[i-1])*np.cos(alpha_list[i-1])
    T_martix[1,2] = -1*np.sin(alpha_list[i-1])
    T_martix[1,3] = -1*np.sin(alpha_list[i-1])*d_list[i-1]
    
    T_martix[2,0] = np.sin(theta_list[i-1])*np.sin(alpha_list[i-1])
    T_martix[2,1] = np.cos(theta_list[i-1])*np.sin(alpha_list[i-1])
    T_martix[2,2] = np.cos(alpha_list[i-1])
    T_martix[2,3] = np.cos(alpha_list[i-1])*d_list[i-1]
    
    T_martix[3,0] = 0
    T_martix[3,1] = 0 
    T_martix[3,2] = 0
    T_martix[3,3] = 1
    
    return T_martix

          那么对于连续的 Link transformations ：

通过python代码表示：

# 例：T_0_1表示坐标系{0}到坐标系{1}的转换矩阵
    T_0_1 = Link_Transformation(0,1,a_list,alpha_list,d_list,theta_list)
    T_1_2 = Link_Transformation(1,2,a_list,alpha_list,d_list,theta_list)
    T_2_3 = Link_Transformation(2,3,a_list,alpha_list,d_list,theta_list)
    T_3_4 = Link_Transformation(3,4,a_list,alpha_list,d_list,theta_list)
    T_4_5 = Link_Transformation(4,5,a_list,alpha_list,d_list,theta_list)
    T_5_6 = Link_Transformation(5,6,a_list,alpha_list,d_list,theta_list)
    
    T_0_6 = T_0_1*T_1_2*T_2_3*T_3_4*T_4_5*T_5_6

根据上面的完整的改进DH参数表，完整的Python计算转换矩阵的代码如下：

import numpy as np


def Link_Transformation(last_i,i,a_list,alpha_list,d_list,theta_list):
    """
    function：坐标系{i-1}到坐标系{i}的转换矩阵
    tips：这里的last_i指的是i-1
    """
    i = i  # 下面使用的i-1表示列表的第i-1个数，注意同DH参数里的i-1区别
    T_martix = np.mat(np.zeros((4,4)))
    
    T_martix[0,0] = np.cos(theta_list[i-1])
    T_martix[0,1] = -1*np.sin(theta_list[i-1])
    T_martix[0,2] = 0
    T_martix[0,3] = a_list[i-1]
    
    T_martix[1,0] = np.sin(theta_list[i-1])*np.cos(alpha_list[i-1])
    T_martix[1,1] = np.cos(theta_list[i-1])*np.cos(alpha_list[i-1])
    T_martix[1,2] = -1*np.sin(alpha_list[i-1])
    T_martix[1,3] = -1*np.sin(alpha_list[i-1])*d_list[i-1]
    
    T_martix[2,0] = np.sin(theta_list[i-1])*np.sin(alpha_list[i-1])
    T_martix[2,1] = np.cos(theta_list[i-1])*np.sin(alpha_list[i-1])
    T_martix[2,2] = np.cos(alpha_list[i-1])
    T_martix[2,3] = np.cos(alpha_list[i-1])*d_list[i-1]
    
    T_martix[3,0] = 0
    T_martix[3,1] = 0 
    T_martix[3,2] = 0
    T_martix[3,3] = 1
    
    return T_martix


if __name__ == "__main__":
    # 初始化参数（DH参数）
    a_list = [0,0,140,100,0,0]
    alpha_list = [0,np.pi/2,0,0,np.pi/2,np.pi/2]
    d_list = [180,0,0,90,80,60]
    theta_list = [0,np.pi/2,0,np.pi/2,-1*np.pi/2,0]  # 输入想要转动的角度（此处设置转动的角度在转动后即达到机械臂伸直状态）
    
    # 例：T_0_1表示坐标系{0}到坐标系{1}的转换矩阵
    T_0_1 = Link_Transformation(0,1,a_list,alpha_list,d_list,theta_list)
    T_1_2 = Link_Transformation(1,2,a_list,alpha_list,d_list,theta_list)
    T_2_3 = Link_Transformation(2,3,a_list,alpha_list,d_list,theta_list)
    T_3_4 = Link_Transformation(3,4,a_list,alpha_list,d_list,theta_list)
    T_4_5 = Link_Transformation(4,5,a_list,alpha_list,d_list,theta_list)
    T_5_6 = Link_Transformation(5,6,a_list,alpha_list,d_list,theta_list)
    
    T_0_6 = T_0_1*T_1_2*T_2_3*T_3_4*T_4_5*T_5_6
    print(T_0_6)
    

得到的解为：

我们再来看一看图片：

 

 因此，我们的DH参数设置的是正确的，Python代码也是正确的！

不跳黄河不死心哈哈哈哈哈哈哈哈哈哈哈哈哈！！！

---

四、回答上文“二/1/（3）”中设置的tips问题）

如果坐标系{2}和坐标系{1}的位置，如下图所示，我们一样进行计算：（图中分成将90分成40-50）

故得到改变后的完整的改进DH参数表：（只有di发生变动）

i	αi-1(alpha_i-1)	ai-1	di	θi	offset
1  {0}-{1}	α0（z0-z1，x0）=0	a0（z0-z1）=0	d1（x0-x1，z1）=180	θ1（x0-x1）=θ1	0
2  {1}-{2}	90	0	50	θ2	90
3  {2}-{3}	0	140	0	θ3	0
4  {3}-{4}	0	100	40	θ4	90
5  {4}-{5}	90	0	80	θ5	-90
6  {5}-{6}	90	0	60	θ6	0

这样一来，我们将代码里的d_list改一下：

d_list = [180,50,0,40,80,60]

然后我们再运行一下程序，得到的答案为：

 是和之前的结果一模一样的。结论就是，建立的坐标系其实是不唯一的！合理就是真理！

撒花……