java集合图解源码系列【2】:从二叉树讲到TreeMap,一篇搞明白树的数据结构
大家好!我是未来村村长,就是那个“请你跟我这样做,我就跟你这样做!”的村长!
||Data Structure||
未来村村长正推出一系列【Data Structure】文章,将从解读数据结构的角度上分析Java集合的源码。因为CSDN上的大多数描述java集合的文章,关注点在于其源码和方法,很少从对数据结构的讲解为切入点进行分析。以此为契机,未来村村长希望能从数据结构开始讲起,分析java集合是如何使用和如何实现的。
文章目录
-
- ||Data Structure||
- 一、二叉树
-
- 1、二叉树的定义
-
- (1)满二叉树
- (2)完全二叉树
- (3)二叉树的表示方式
- ① 数组表示法
- ② 链表表示法
- 2、二叉树的遍历
- 二、二叉XX树
-
- 1、二叉排序树、二叉搜索树和二叉查找树(Binary Search Tree)
-
- (1)插入
- (2)删除
- (3)排序二叉树的不平衡
- 2、平衡二叉树和AVL树(Balanved Binary Tree)
-
- (1)左旋:旧节点去左边
-
- ① 右右型
- ② 右左型
- (2)右旋:旧节点去右边
-
- ① 左左型
- ② 左右型
- 3、B树与B+树
-
- (1)B树和B-树
- (2)B+树
- 三、红黑树
-
- 1、红黑树定义
- 2、红黑树自平衡操作
-
- (1)左旋
- (2)右旋
- 四、TreeMap
-
- 1、概念性源码
-
- (1)基本属性
- (2)节点Entry类
- 2、方法性源码
-
- (1)put方法
-
- ① put()
- ② fixAfterInsertion()
- ③ rotateLeft()
- ④ rotateRight()
- (2)remove方法
- (3)get方法
在正式开始前,我们可以回顾一下树的相关术语(不同的课本对其定义不同,我们这里不必纠结):
-
树的度:所有结点的度的最大值
-
树的深度:结点层次的最大值,层次为0的树只有一个根节点
-
树的高度:树的深度+1
-
节点的层次:根结点的层次规定为0,则其它结点的层次是其双亲结点层次+1
-
节点的度:结点所拥有的子树(或者孩子结点)的个数
-
叶节点:度为0(无子树)
-
子节点、双亲节点、兄弟节点:字面意思
-
森林:树的集合
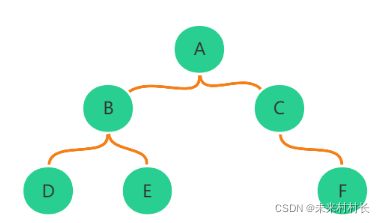
一、二叉树
1、二叉树的定义
二叉树,直接从字面来理解,节点的度小于等于2的树,即一个节点最多只有两个子节点。二叉树中又有特殊的二叉树。
(1)满二叉树
如果二叉树的高度为h,树的结点数为2h-1,h>=0。就是把高度为h的树装满。
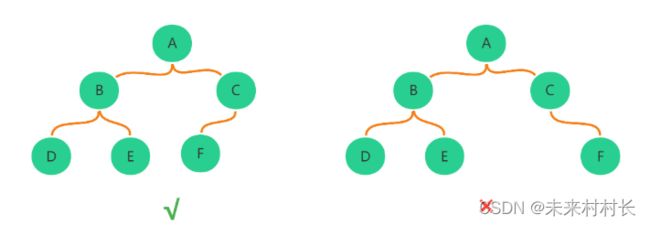
(2)完全二叉树
如果二叉树的高度为h,树的结点数小于2h-1,h>=0,但其编号方式和排列方式按照从左到右、从上到下的顺序一一对应。
(3)二叉树的表示方式
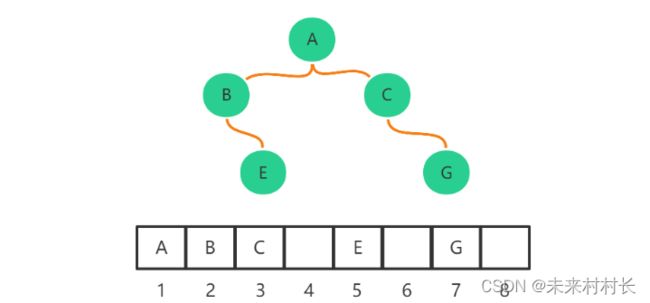
① 数组表示法
可以使用有序的一维数组表示二叉树,我们从下图可以看见节点之间的关系。
父节点的子节点的在数组中的位置关系:2x和2x+1(根节点x为1,x为父节点所在位置),若从0开始,关系则为2x+1和2x+2。具体代码实现不提供了,我们主要看链表表示。
② 链表表示法
链表表示法我们甚至图都不用画,该方法将树的每一个节点看作一个Node,双亲节点存放着指向子节点的left_Node和right_Node。我们来看看代码实现。
1.定义节点
//首先定义节点
class TreeNode{
int value;//节点存放的数据
TreeNode left_Node;//左子节点
TreeNode right_Node;//右子节点
//节点构造方法
public TreeNode(int value){
this.value = value;
this.left_Node=null;
this.right_Node=null;
}
}
2.链表实现
//建立二叉树
class BinaryTree{
public TreeNode rootNode;//根节点
public void add(int value){
TreeNode<E> currentNode = rootNode;//游标指向根节点
//若根节点为空,则数据放入根节点
if(rootNode==null){
rootNode = new TreeNode(value);
return;
}
//若不为空,我们这里默认将大于双亲节点的子节点放在右边,实际上二叉树无此要求
while(ture){
if(value<current.value){//若小于则放在左边
if(current.value.left_Node==null){//
currentNode.left_Node = new TreeNode(value)
return;
}//若不为空,我们继续寻找
else currentNode = currentNode.left_Node;
}
else{//同理
if(current.value.right_Node==null){
currentNode.right_Node = new TreeNode(value)
return;
}
else currentNode = currentNode.right_Node;
}
}}}}
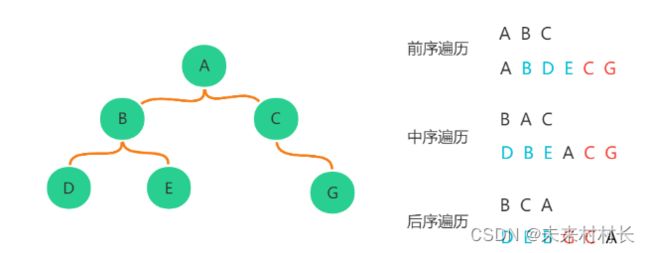
2、二叉树的遍历
前序遍历,每次都按照 双亲节点-左子节点-右子节点 顺序,逐层遍历。
中序遍历,每次都按照 左子节点-双亲节点-右子节点 顺序,逐层遍历。
后续遍历,每次都按照 左子节点-右子节点-双亲节点 顺序,逐层遍历。
其算法实现也很简单:
public void PreOrder(TreeNode node){
if(node!=null){
System.out.print(node.value);
PreOrder(node.left_Node);
PreOrder(node.right_Node);
}
//中序遍历
public void Order(TreeNode node){
if(node!=null){
Order(node.left_Node);
System.out.print(node.value);
Order(node.right_Node);
}
//后序遍历
public void Order(TreeNode node){
if(node!=null){
Order(node.left_Node);
Order(node.right_Node);
System.out.print(node.value);
}
学过JVM我们知道,方法的调用是位于java栈(虚拟栈和本地栈)中处理,当出现递归方法时,会递归到最后一个方法才开始逆序执行。所以在执行后序遍历时,要执行完所有Order()方法,才会到最顶层的Order方法,执行根节点value的的打印。
二、二叉XX树
1、二叉排序树、二叉搜索树和二叉查找树(Binary Search Tree)
二叉排序树、二叉搜索树、二叉查找树是同一种树,我们称其为BST树,该树是许多树的基础。其定义我们之前在二叉树的代码实现时已经体现过,我们当时是按照左子树结点值<根结点值<右子树结点值的顺序进行添加操作,即小左大右。这样使用中序遍历可获得一个递增的有序序列。
(1)插入
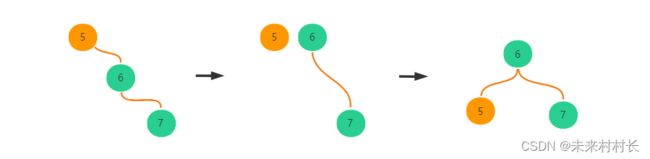
我们来看看二叉排序树的插入过程。在下图中,我们看到每次插入节点从根节点开始遍历,与根节点比较值的大小,大于根节点向右移动,然后6<7,向左移动,就找到了对应的插入位置。
(2)删除
被删结点具有以下三种情况:
- 被删结点是叶结点(左、右子树都空 ):只需要将其双亲节点指向他的节点赋值为null即可。
- 被删结点只有1个孩子结点 (左子树空或右子树空):只需要将其双亲节点指向他的节点直接指向其被删除节点的孩子节点即可
- 被删结点有2个孩子结点(左、右子树都不空):若直接选择一个子节点替换被删除的节点,可能会导致其不满足排序二叉树的属性,我们可以选择其左子树最大的的节点或右子树最小的节点来替换该节点。
(3)排序二叉树的不平衡
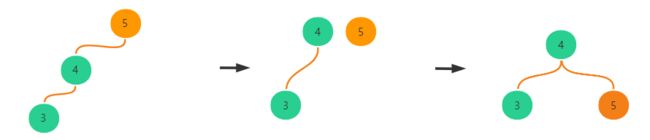
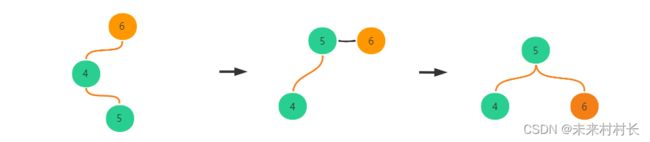
当插入顺序是从小到大的顺序插入时,就容易产生下图情况,从大到小插入同理。
2、平衡二叉树和AVL树(Balanved Binary Tree)
平衡二叉树、AVL树是同一种树,由AV和L(首字母缩写)发明的平衡树,它基于二叉树做了优化,其需要满足以下条件:
- 符合二叉树的性质
- 对于每个子树,左右子树的高度差小于等于 1
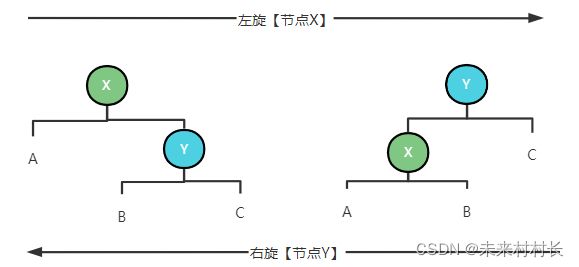
当二叉排序树不满足该条件时,其添加了左旋和右旋的算法,我们来看看具体是怎么实现。
(1)左旋:旧节点去左边
- 旧根节点为新根节点的左子树
- 新根节点的左子树(如果存在)为旧根节点的右子树
① 右右型
② 右左型
(2)右旋:旧节点去右边
- 旧根节点为新根节点的右子树
- 新根节点的右子树(如果存在)为旧根节点的左子树
① 左左型
② 左右型
具体的算法实现和更复杂的情况,我们将在红黑树与TreeMap代码中讲解。
3、B树与B+树
B树和B+树的出现是因为另外一个问题,那就是磁盘IO;IO操作的效率很低,那么,当在大量数据存储中,查询时我们不能一下子将所有数据加载到内存中,只能逐一加载磁盘页,每个磁盘页对应树的节点。造成大量磁盘IO操作(最坏情况下为树的高度)。平衡二叉树由于树深度过大而造成磁盘IO读写过于频繁,进而导致效率低下。
(1)B树和B-树
B树和B-树是同一种树,其结构如下图。2-3-4树是阶数为4的B树,则每个双亲节点的子节点数量为2-4个,如下图。
(2)B+树
MySQL的索引数据结构。B+树的磁盘读写代价更低,便于范围查询,B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题,正是为了解决这个问题,B+树应运而生。
B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作或者说效率太低;B+树的节点只存储索引key值,具体信息的地址存在于叶子节点的地址中。这就使以页为单位的索引中可以存放更多的节点。减少更多的I/O支出。
总结B+树对于B树的优点:
-
单一节点存储更多的元素,使得查询的IO次数更少;
-
所有查询都要查找到叶子节点,查询性能稳定;
-
所有叶子节点形成有序链表,便于范围查询。
B+树缺点:
-
主键不是有序递增的,导致每次插入数据产生大量的数据迁移和空间碎片
-
大量写请求的分布是随机的。
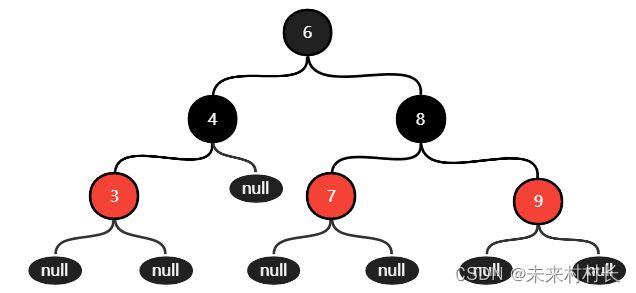
三、红黑树
红黑树基于二叉搜索树,AVL树的查找、插入和删除在平均和最坏情况下都是O(logn),但是其左旋和右选的成本消耗过高,从而出现了改良版AVL树——红黑树。红黑树是对概念模型2-3-4树的一种实现,由于直接进行不同节点间的转化会造成较大的开销,所以选择以二叉树为基础,在二叉树的属性中加入一个颜色属性来表示2-3-4树中不同的节点。(很多书中会说是由黑色节点指出的红色链接,链接指向的节点颜色为红,但是我们以节点颜色来定义)
1、红黑树定义
- 根节点是黑色,其余节点要么黑色要么红色
- 每个红色节点必须有两个黑色子节点
- 所有叶子节点皆为黑色
- 从任一节点到其每个叶子节点的所有简单路径上的黑色节点数量相同
- 插入的新节点为红色
2、红黑树自平衡操作
- 变色:在不违反上述红黑树规则特点情况下,将红黑树某个node节点颜色由红变黑,或者由黑变红;
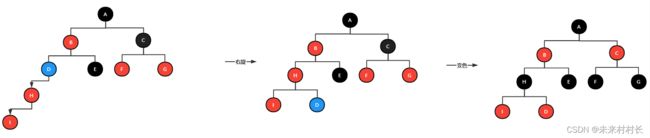
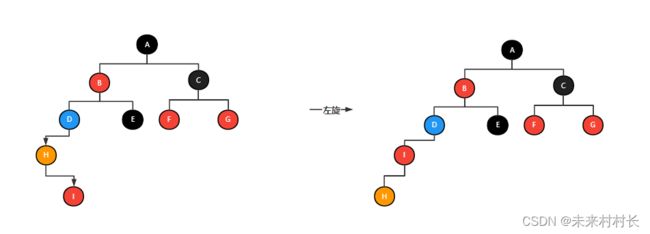
- 左旋:对双亲向左旋转一位,其右子节点成为其双亲节点,此时该右子节点有三个节点,则需要将该右子节点的左子节点放置原双亲节点的右子节点。(右子节点当爸爸,右边左孙变右子)
- 右旋:对双亲向右旋转一位,其左子节点成为其双亲节点,此时该左子节点有三个节点,则需要将该左子节点的右子节点放置原双亲节点的左子节点。(左子节点当爸爸,左边右孙变左子)
(1)左旋
public void leftRotate(Node root) {
Node node=new Node(root.value);
node.left=root.left;
node.right=root.right.left;
root.value=root.right.value;
root.right=root.right.right;
root.left=node;
}
(2)右旋
public void rightRotate(Node root) {
//创建新节点
Node node = new Node(root.value);
//操作新节点
node.left=root.left.right;
node.right=root.right;
//修改当前节点
root.value=root.right.value;
root.left=root.left.left;
root.right=node;
}
四、TreeMap
1、概念性源码
(1)基本属性
public class TreeMap<K,V>{
//根节点
private transient Entry<K,V> root;
//Key-value键值对的数量
private transient int size = 0;
//红黑树结构的调整次数
private transient int modCount = 0;
//定义红色节点和黑色节点常量【boolean】
private static final boolean RED = false;
private static final boolean BLACK = true;
//用于维护此树映射中的顺序的比较器,如果使用其键的自然顺序,则为null。
private final Comparator<? super K> comparator;
}
(2)节点Entry类
static final class Entry<K,V> implements Map.Entry<K,V> {
//key,val是存储的原始数据
K key;
V value;
//定义了节点的左孩子
Entry<K,V> left;
//定义了节点的右孩子
Entry<K,V> right;
//通过该节点可以反过来往上找到自己的父亲
Entry<K,V> parent;
//默认情况下为黑色节点,可调整
boolean color = BLACK;
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
//获取key
public K getKey() {return key;}
//获取Value
public V getValue() {return value;}
//更换value的值,并返回原来的值
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}
属性类源码,较好理解,通过文中源码的注释即可理解。
2、方法性源码
(1)put方法
① put()
public V put(K key, V value) {
Entry<K,V> t = root;//给t赋值root
//如果根节点为null,则创建新的Entry赋值给根节点,调整次数+1
if (t == null) {
compare(key, key);
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;//临时变量,用来判断比较值的大小
Entry<K,V> parent;
//cpr表示有无自己定义的排序规则,分两种情况遍历执行
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);//key为传入的key,t最初为root
if (cmp < 0)//小左
t = t.left;
else if (cmp > 0)//大右
t = t.right;
else//相等设值
return t.setValue(value);
} while (t != null);
}
else {
//从这里看出,当默认排序时,key值是不能为null的
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
//该处同上
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//若没有找到相应的key,则新建一个Entry
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
//加入节点后可能会造成红黑树的结构受到破坏,我们要使用fixAfterInsertion()方法进行调整
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
② fixAfterInsertion()
插入后调整一共有以下几种情况:
| 无需调整 | 【变色】即可实现平衡 | 【旋转+变色】才可实现平衡 | |
|---|---|---|---|
| 情况1: | 当父节点为黑色时插入子节点 | 空树插入根节点,将根节点红色变为黑色 | 父节点为红色左节点,叔父节点为黑色,插入左子节点,那么通过【左左节点旋转】 |
| 情况2: | - | 父节点和叔父节点都为红色 | 父节点为红色左节点,叔父节点为黑色,插入右子节点,那么通过【左右节点旋转】 |
| 情况3: | - | - | 父节点为红色右节点,叔父节点为黑色,插入左子节点,那么通过【右左节点旋转】 |
| 情况4: | - | - | 父节点为红色右节点,叔父节点为黑色,插入右子节点,那么通过【右右节点旋转】 |
调整的话,是因为插入新节点是会破坏红黑树的结构,所以需要进行调整。有以下五种情况:
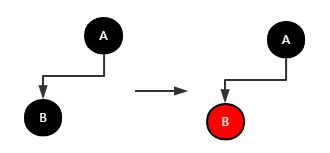
无需调整
当父节点为黑色时,插入子节点,对于插入的子节点我们将其默认的black改为red。
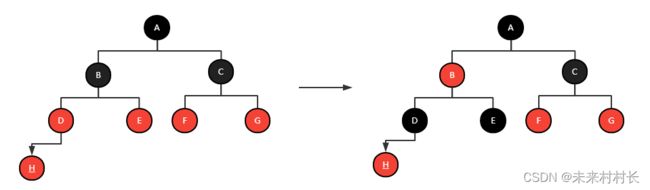
变色
当父节点和叔父节点都为红色时
旋转+变色
【蓝色代表祖父节点,黄色代表父节点】
A:左左型——父节点为红色左节点,叔父节点为黑色(或NULL),插入左节点
A处理:将其祖父节点进行右旋操作,然后进行变色。
B:左右型——父节点为红色左节点,叔父节点为黑色,插入右节点
B处理:将其父节点进行左旋,叔父节点进行右旋
C:右右型——同理但相反,类推即可
D:右左型——同理但相反,类推即可
(PS:以上图片大小不一致,我看着也很难受,各位点开再看吧)
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
③ rotateLeft()
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
④ rotateRight()
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
(2)remove方法
public V remove(Object key) {
Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) {//这种情况就不用多说了吧
root = null;
} else {
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else {
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
(3)get方法
public V get(Object key) {
Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
final Entry<K,V> getEntry(Object key) {
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}
final Entry<K,V> getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator<? super K> cpr = comparator;
if (cpr != null) {
Entry<K,V> p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
}