OpenCV实现常见的四种图像几何变换

目录

• 准备图片
• 1. 缩放 cv2.resize()方法
• 2. 翻转 cv2.flip()方法
• 3. 仿射变换 warpAffine()方法
• 3.1 平移
• 3.2 旋转
• 3.3 倾斜
• 4. 透视

准备图片

选择一张shape为(500,500,3)的梵高的《星月夜》以便示例。

1. 缩放 cv2.resize()方法

cv2.resize(src, dsize, dst=None, fx=None, fy=None, interpolation=None)

src 原图（的数组）

dsize: 输出图像的大小 格式：(a,b)。

设定dsize后就无需再设置fx和fy

fx 可选参数 水平方向缩放比

fy 可选参数 垂直方向缩放比

fx和fy不同于dsize，fx和fy是各是一个比值，如设为2，则表示放大2倍，设为1/2则表示缩小到原来的1/2

import cv2
img = cv2.imread("The_Starry_Night.jpg")

dst1 = cv2.resize(img, (200, 200))
dst2 = cv2.resize(img, (900, 900))
cv2.imshow("img", img)
cv2.imshow("dst1", dst1)
cv2.imshow("dst2", dst2)
cv2.waitKey()
cv2.destroyAllWindows()

执行结果如图所示，相比原图，图像得到了指定大小的缩小与放大。

使用fx和fy参数，则需要手动把dsize设为None。

import cv2
img = cv2.imread("The_Starry_Night.jpg")  
# 将宽缩小到原来的1/3、高缩小到原来的1/2
dst3 = cv2.resize(img, None, fx=1 / 3, fy=1 / 2) 
# 将宽高扩大2倍
dst4 = cv2.resize(img, None, fx=2, fy=2)  
cv2.imshow("img", img)
cv2.imshow("dst3", dst3) 
cv2.imshow("dst4", dst4) 
cv2.waitKey() 
cv2.destroyAllWindows()  

结果呈现：

2. 翻转 cv2.flip()方法

flip(src, flipCode, dst=None)

src 图像（数组）

flipCode 翻转代码。可以是0，正数，负数。0表示沿X轴（水平方向的轴）翻转。1表示沿Y轴（竖直方向的轴）翻转。

负数表示同时沿X轴和Y轴翻转。

讲原图经过着三种翻转后，与原图拼在一块，呈现出了这种奇观：

import cv2
img = cv2.imread("The_Starry_Night.jpg")
dst1 = cv2.flip(img, 0)
dst2 = cv2.flip(img, 1)
dst3 = cv2.flip(img, -1)
cv2.imshow("img", img)
cv2.imshow("dst1", dst1)
cv2.imshow("dst2", dst2)
cv2.imshow("dst3", dst3)
cv2.waitKey()
cv2.destroyAllWindows()

将翻转结果放在同一张画布中

import cv2
import numpy as np
img = cv2.imread("The_Starry_Night.jpg")
dst1 = cv2.flip(img, 0)
dst2 = cv2.flip(img, 1)
dst3 = cv2.flip(img, -1)
a, b, c = img.shape
canvas = np.ones((2 * a, 2 * b, c), np.uint8) * 255
canvas[0:b, 0:a] = img
canvas[b:2*b, 0:a] = dst1
canvas[0:b, a:2*a] = dst2
canvas[b:2*b, a:2*a] = dst3
cv2.imshow("pic", canvas)
cv2.waitKey()
cv2.destroyAllWindows()
# 保存图片
# cv2.imwrite("final_pic", canvas)

结果呈现：

3. 仿射变换 warpAffine()方法

常见的仿射变换有平移，旋转和倾斜变换。

仿射变换使用cv2.warpAffine()方法完成

warpAffine(src, M, dsize, dst=None, flags=None, borderMode=None, borderValue=None)

src 原图

M 是一个二行三列的矩阵，也称仿射矩阵。warpAffine方法根据此矩阵的值来变换像素的位置。

M = [[a, b, c], [d, e, f]]，则像素的变换公式为：

X = x × a + y × b + c

Y = x × d + y × e + f

其中x,y指原像素的x、y轴坐标。X,Y指变换后的X,Y坐标。

dsize 输出图像的尺寸。（不带放缩，增大的部分用黑色色素(0)填充）

这三个参数是常用的参数。其余参数建议使用默认值。

flags表示插入方式，borderMode是边界类型，borderValue表示边界值（默认0）。dst表示反射变换后输出的图像。

3.1 平移

以将《星月夜》向左平移50个像素，向下平移100个像素为例。

则M数组应写为[[1, 0, 50], [0, 1, 100]]：

import cv2
import numpy as np
img = cv2.imread("The_Starry_Night.jpg")
rows = len(img)
cols = len(img[0])
M = np.float32([[1, 0, 50],
                [0, 1, 100]]) 
dst = cv2.warpAffine(img, M, (cols, rows))
cv2.imshow("img", img) 
cv2.imshow("dst", dst) 
cv2.waitKey() 
cv2.destroyAllWindows()

如图所示，图像按照我们的预期成功被平移。

只是这样得到的图像有色素损失，我们丢失了超出画布之外的数据。

为了避免损失，可以取设置dsize参数来控制输出图像的大小。

修改后的代码如下：

import cv2
import numpy as np
img = cv2.imread("The_Starry_Night.jpg")
rows = len(img)
cols = len(img[0])
M = np.float32([[1, 0, 50],
                [0, 1, 100]])
dst = cv2.warpAffine(img, M, (cols+200, rows+200))
cv2.imshow("img", img)
cv2.imshow("dst", dst)
cv2.waitKey()
cv2.destroyAllWindows()

优化后的程序执行效果：

3.2 旋转

旋转也是通过M矩阵来实现的，这个矩阵的运算较复杂，

OpenCV提供了getRotationMatrix2D()方法来计算旋转操作的M矩阵

getRotationMatrix2D(center, angle, scale)

center 指旋转中心的坐标

angle指旋转的角度

scale值缩放的比例。（旋转过程支持缩放）

import cv2
img = cv2.imread("The_Starry_Night.jpg")
rows = len(img) 
cols = len(img[0]) 
center = (rows / 2, cols / 2) 
M = cv2.getRotationMatrix2D(center, 30, 0.8) 
dst = cv2.warpAffine(img, M, (cols, rows)) 
cv2.imshow("img", img) 
cv2.imshow("dst", dst) 
cv2.waitKey() 
cv2.destroyAllWindows()  

旋转效果如图所示：

3.3 倾斜

OpenCV需要定位到图像的三个点的位置来计算倾斜效果，即左上角，右上角和左下角。

图像的倾斜也是根据M矩阵实现，得出矩阵的运算较复杂，通过getAffineTransform 方法实现。

语法

getAffineTransform(src, dst)

src是原图像的左上角，右上角和左下角三个点的坐标。三维数组格式，形如[[a, b], [c, d], [e, f]]。

dst是倾斜后这三个点预期的坐标。格式同上。

要保持左上，右下，左下三个点的顺序不能乱。

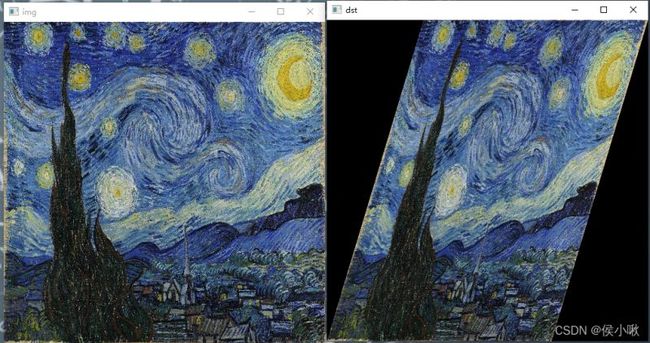
以将《星月夜》保持左下角和右上角坐标不变，左上角（(0,0)处）向右移动150个像素长度。

代码如下：

import cv2
import numpy as np
img = cv2.imread("The_Starry_Night.jpg")
rows = len(img)
cols = len(img[0])
p1 = np.array([[0, 0], [cols - 1, 0], [0, rows - 1]], dtype=np.float32)
p2 = np.array([[150, 0], [cols - 1, 0], [0, rows - 1]], dtype=np.float32)
M = cv2.getAffineTransform(p1, p2)
dst = cv2.warpAffine(img, M, (cols, rows))
cv2.imshow('img', img)
cv2.imshow('dst', dst)
cv2.waitKey()
cv2.destroyAllWindows()

程序执行效果如下：

4. 透视

透视的实现使用的是warpPerspective()方法，而不再是用于平移、旋转、倾斜的warpAffine()方法。

使用warpPerspective()方法也需要通过M矩阵来计算透视效果，计算透视的M矩阵可以使用getPerspectiveTransform()方法。

getPerspectiveTransform(src, dst, solveMethod=None)

该方法常用的参数有两个，分别为原图的四个点的坐标(scr) 和 透视后四个点的坐标(dst)。Opcv需要通过定位图像的这四个点来计算透视效果。四个点依次为左上，右上，左下，右下。

坐标格式为二维数组格式，形如[[a, b],[c, d],[e, f],[g, h]]。

示例代码如下：

import cv2
import numpy as np
img = cv2.imread("The_Starry_Night.jpg")
rows = len(img)
cols = len(img[0])
# 原图的四点坐标
p1 = np.zeros((4, 2), np.float32)
p1[0] = [0, 0]
p1[1] = [cols - 1, 0]
p1[2] = [0, rows - 1]
p1[3] = [cols - 1, rows - 1]
# 透视后的四点坐标
p2 = np.zeros((4, 2), np.float32)
p2[0] = [150, 0]
p2[1] = [cols - 150, 0]
p2[2] = [0, rows - 1]  # 不变
p2[3] = [cols - 1, rows - 1]  # 不变
M = cv2.getPerspectiveTransform(p1, p2)
dst = cv2.warpPerspective(img, M, (cols, rows))
cv2.imshow('The_Starry_Night', img)
cv2.imshow('The_Starry_Night2', dst)
cv2.waitKey()
cv2.destroyAllWindows()

展示原图和透视后的图像效果：

到此这篇关于OpenCV实现常见的四种图像几何变换的文章就介绍到这了,更多相关OpenCV图像几何变换内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！