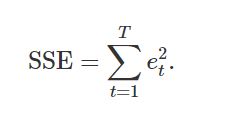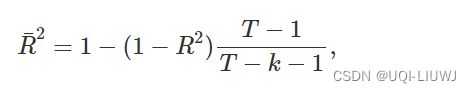机器学习笔记:(时间序列中的线性回归)如何选择预测变量
当有许多可能的预测变量时,我们需要一些策略来选择用于回归模型的最佳预测变量。
1 不推荐的方法
不推荐的一种常见方法是针对特定预测变量绘制预测结果和预测变量之间的关系图,如果没有明显的关系,则从模型中删除该预测变量。
这是不一定有用的,因为并不总是可以从散点图中看到关系,尤其是在未考虑其他预测变量的影响时。
另一种同样无效的常见方法是对所有预测变量进行多元线性回归,并忽略 p 值大于 0.05 的所有变量。
2 本篇前言
在本篇中,我们将使用预测准确性的度量。在R语言中,使用CV()函数实现
y<-ts(c(5,3,3.1,3.2,3.3,3.4,3.5,3.3,3.2,4,4.1,4.2,
6,4,4.1,4.2,4.3,4.4,4.5,4.6,4.7,4.8,4.9,5,
10,9,8,8.5,8.4,8.5,8.6,8.7,8.8,8.9,9,9.5),
start = 2020,
frequency = 12)
library(forecast)
CV(tslm(y~y))
# CV AIC AICc BIC AdjR2
# 5.690735 64.569914 64.933550 67.736952 0.000000 我们将这些值在选择不同预测变量的模型之间进行比较。
对于 CV(R语言中MSE的说法)、AIC、AICc 和 BIC 度量,我们希望找到具有最小值的模型;
对于adjusted R2,我们寻找具有最大值的模型。
3 R2 与adjusted R2
回归模型的R2 值并不是衡量模型预测能力的好方法。 它衡量模型与历史数据的拟合程度,而不是模型预测未来数据的程度。
此外,R2 不允许“自由度”。 添加任何变量都会增加 R2 的值,即使该变量无关紧要。 由于这些原因,预测者不应使用 R2 来确定模型是否会给出良好的预测,因为它会导致过度拟合。
一个等效的想法是选择给出最小误差平方和 (SSE) 的模型,由下式给出
但是,最小化 SSE 等效于最大化 R2,并且总是会选择具有最多变量的模型,因此不是选择预测变量的有效方法。
旨在克服这些问题的替代方案是调整后的 R2(也称为“R-bar-squared”):
其中 T 是观察数,k是预测变量数。 这是对![]() 的改进,因为它不再随着每个添加的预测变量而增加。 使用这个度量,最好的模型将是具有最大
的改进,因为它不再随着每个添加的预测变量而增加。 使用这个度量,最好的模型将是具有最大![]() 的模型。 最大化
的模型。 最大化![]() 等效于最小化标准误差
等效于最小化标准误差  。
。
4 赤化信息准则 Akaike’s Information Criterion
一个和adjusted R^2密切相关的方法是 Akaike 信息准则
T 是用于估计的观测数,k 是模型中的预测变量数。
不同的计算机包对 AIC 的定义略有不同,尽管它们都应该导致选择相同的模型。
这里的 k+2 部分是因为模型中有 k+2 个参数:预测变量的 k 个系数、截距和残差的方差。 (有些地方比如算法笔记:ARIMA_UQI-LIUWJ的博客-CSDN博客 就直接使用k了【同时那个博客中,L指的是似然函数,所以是希望越大越好,这边是误差之和SSE,希望越小越好】)
这里的想法是用需要估计的参数数量来惩罚模型的拟合(SSE)。
我们的目标是让AIC越小越好,也就是模型的参数(k)越少越好(模型越简单越好),同时模型的误差(SSE)越小越好
4.1 修正的池化准则
对于较小的 T 值,AIC 倾向于选择过多的预测变量,因此开发了 AIC 的偏差校正版本,
与 AIC 一样,AICc 应该被最小化。
5 施瓦茨贝叶斯信息理论 Schwarz’s Bayesian Information Criterion
与 AIC 一样,最小化 BIC 旨在提供最佳模型。
BIC 选择的模型要么与 AIC 选择的模型相同,要么比AIC具有更少的项。 这是因为 BIC 对参数数量的惩罚比 AIC 更重。
6 使用哪种准则来选择模型(参数)?
虽然![]() 被广泛使用,并且比其他度量存在的时间更长,但它倾向于选择相对更多的预测变量使其不太适合预测。
被广泛使用,并且比其他度量存在的时间更长,但它倾向于选择相对更多的预测变量使其不太适合预测。
许多统计学家喜欢使用 BIC,因为它的特点是,如果存在真正的基础模型,BIC 会在有足够数据的情况下选择该模型。 然而,实际上,很少有真正的基础模型,即使有真正的基础模型,选择该模型也不一定能提供最佳预测(因为参数估计可能不准确)。
因此,我们建议使用 AICc、AIC或CV,其中每个统计数据都以预测为目标。 如果 T 的值足够大,它们都会导致相同的模型。
7 举例说明
在预测美国消费的多元回归示例中,我们考虑了四个预测变量。 有四个预测变量,就有 16 个可能的模型。
现在我们可以检查所有四个预测变量是否真的有用,或者我们是否可以删除其中一个或多个。
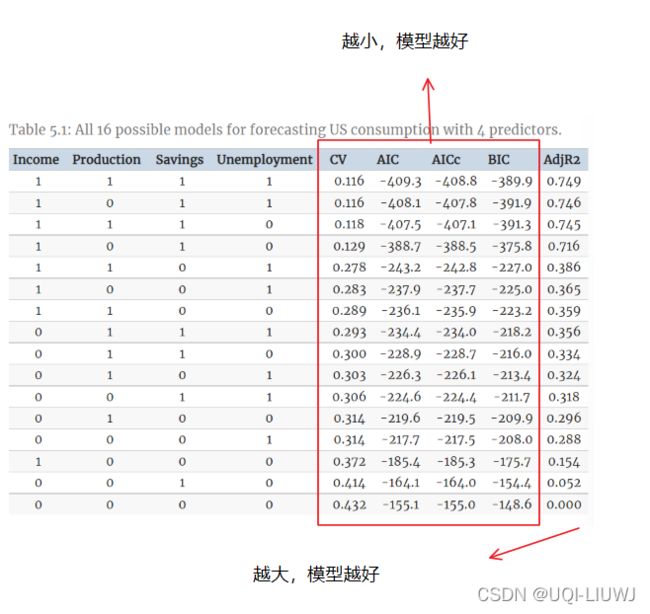
所有 16 个模型均已拟合,结果汇总在表 5.1 中。 “1”表示预测变量包含在模型中,“0”表示预测变量未包含在模型中。
最好的模型包含所有四个预测变量。 然而,仔细观察结果会发现一些有趣的特征。
前四行的模型和下面的模型之间有明显的区别。 这表明收入和储蓄都是比生产和失业更重要的变量。
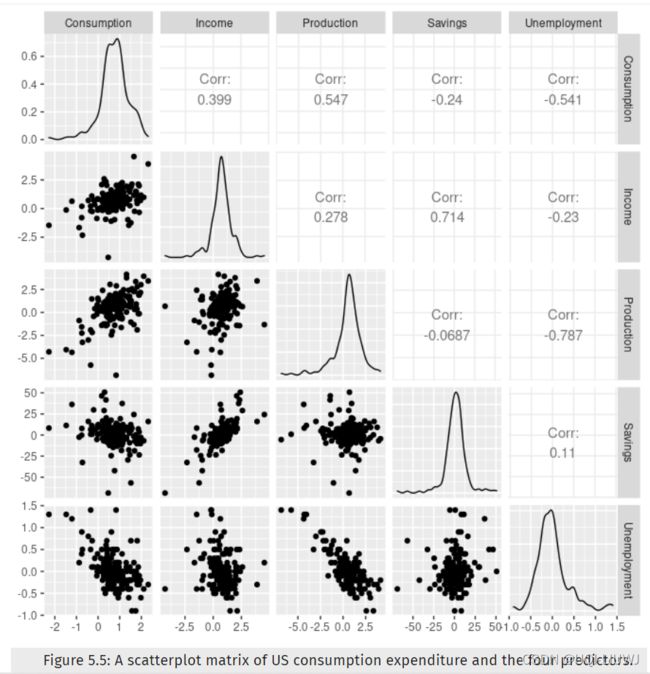
此外,前两行的 CV、AIC 和 AICc 值几乎相同。 因此,我们可能会删除 Production 变量并获得类似的预测。 请注意,Production 和 Unemployment 高度(负)相关,如图 5.5 所示【第五行第三列】,因此 Production 中的大部分预测信息也包含在 Unemployment 变量中。
8 best subset regression
在可能的情况下,应拟合所有潜在的回归模型(如上面示例中所做的那样),并应根据所讨论的措施之一选择最佳模型。 这被称为“最佳子集”回归或“所有可能的子集”回归。
8.1 逐步回归
如果有大量预测变量,则不可能拟合所有可能的模型。 因此,需要一种策略来限制要探索的模型的数量。
一种效果很好的方法是向后逐步回归backwards stepwise regression :
- 从包含所有潜在预测变量的模型开始。
- 一次删除一个预测变量。 如果模型提高了预测准确性的度量,请保留该模型。
- 迭代直到没有进一步的改进。
如果潜在预测变量的数量太大,则后向逐步回归将不起作用,可以使用前向逐步回归代替forward stepwise regression。
此过程从仅包含截距的模型开始。 一次添加一个预测变量,模型中保留最能提高预测准确性度量的预测变量。 重复该过程,直到无法获得进一步的改善。
或者,对于向后或向前回归方向,起始模型可以是包含潜在预测变量子集的模型。
在这种情况下,无论前向还是后向传播,都需要包括一个额外的步骤。
对于后向过程,我们还应该考虑在每个步骤中是否添加一个预测
对于前向过程,我们还应该考虑在每个步骤中是否删除一个预测变量。
这些被称为混合方法。
任何逐步的方法都不能保证产生最好的模型,但它几乎总是会产生一个好的模型
参考内容
5.5 Selecting predictors | Forecasting: Principles and Practice (2nd ed) (otexts.com)