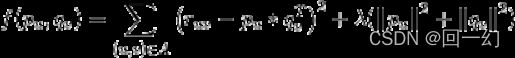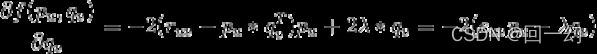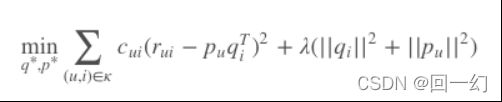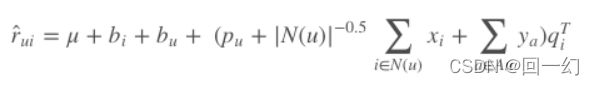推荐算法——矩阵分解
1、矩阵分解
矩阵分解是指将一个矩阵分解成两个或者多个矩阵的乘积,实际推荐计算时不再使用大矩阵,而是用分解得到的两个小矩阵:一个是由代表用户偏好的用户隐因子向量组成,另一个是由代表物品语义主题的隐因子向量组成。
对于下图的user-item矩阵(评分矩阵),记为Rm×n。可以将其分解成两个或者多个矩阵的乘积,假设分解成两个矩阵Pm×k和Qk×n,我们要使得矩阵Pm×k和Qk×n的乘积能够还原原始的矩阵Rm×n。
Rm×n=Pm×k*Qk×n。其中k用k-fold确定。
如下图user-item表中,有用户对每一件商品的打分,其中空白部分表示用户未对该商品进行打分。
矩阵分解的目的是通过机器学习的手段将用户行为矩阵中缺失的数据(用户没有评分的元素)填补完整,最终达到可以为用户做推荐的目标。
2、k-fold简单了解
基本原理:
在机器学习的训练过程中,经常会出现过拟合的问题,就是模型可以很好的匹配训练数据,却不能很好在预测训练集外的数据。如果此时就使用测试数据来调整模型参数,就相当于在训练时已知部分测试数据的信息,会影响最终评估结果的准确性。通常的做法是在训练数据再中分出一部分做为验证(Validation)数据(方法就是:K折交叉验证),用来评估模型的训练效果。
验证数据取自训练数据,但不参与训练,这样可以相对客观的评估模型对于训练集之外数据的匹配程度。模型在验证数据中的评估常用的是交叉验证,又称循环验证。它将原始数据分成K组(K-Fold),将每个子集数据分别做一次验证集,其余的K-1组子集数据作为训练集,这样会得到K个模型。这K个模型分别在验证集中评估结果,最后的误差MSE(Mean Squared Error)加和平均就得到交叉验证误差。交叉验证有效利用了有限的数据,并且评估结果能够尽可能接近模型在测试集上的表现,可以做为模型优化的指标使用。
KFold
KFold(n_splits=’warn’, shuffle=False, random_state=None)
参数:
n_splits:表示划分为几块(至少是2)
Shuffle:表示是否打乱划分,默认False,即不打乱
random_state:表示是否固定随机起点,一般在 shuffle == True时使用.
方法:
1.get_n_splits([X, y, groups]) 返回分的块数
2.split(X[,Y,groups]) 返回分类后数据集的index
举例:
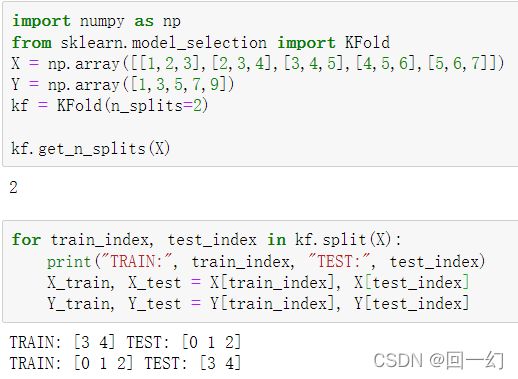
import numpy as np
from sklearn.model_selection import KFold
X = np.array([[1,2,3],[2,3,4],[3,4,5],[4,5,6],[5,6,7]])
Y = np.array([1,3,5,7,9])
kf = KFold(n_splits=2)
kf.get_n_splits(X)
for train_index, test_index in kf.split(X):
print("TRAIN:", train_index, "TEST:", test_index)
X_train, X_test = X[train_index], X[test_index]
Y_train, Y_test = Y[train_index], Y[test_index]结果:
3、SVD奇异值分解
奇异值分解(Singular Value Decomposition,SVD)在降维、数据压缩、推荐系统(在推荐算法中实际使用的是伪奇异值分解)等有广泛的应用,任何矩阵都可以进行奇异值分解。
如下图的稀疏矩阵,矩阵中内容表示用户对物品的评分,其中空白部分表示未知的,也就是要预测的。
矩阵分解把用户(user)和物品(item)都映射到一个K维空间中,分别记作Pm×k和Qk×n,这个k维空间不一定有很好的解释性,每一个维度也没有名字,常叫做隐因子向量。我们并不需要显式的定义这些关联维度,而只需要假定它们存在即可。k的典型取值一般是20到200。
举例:记用户u的向量Pu,物品v的向量Qv,那么物品v推荐给用户u的推荐分数为:Ruv=Pu*Qv。
SVD学习过程如下:
(1)准备好用户物品的评分矩阵,每一条评分数据看做一条训练样本
(2)对分解后的P、Q矩阵做随机初始化值
(3)用P和Q计算预测分数,然后计算与实际分数误差
(4)梯度下降更新P和Q
(5)重复(3)(4),直到达到停止条件
得到U和V后,实际上就是得到了每个用户和每个物品的隐因子向量,只用做点积就可以得到用户和物品的推荐了。
4、算法原理
假设所有用户有评分的(u,v)对(u表示用户,v表示物品)组成的集合为A,![]() ,通过矩阵分解将用户u和标的物品v嵌入k维隐式特征空间的向量分别为:
,通过矩阵分解将用户u和标的物品v嵌入k维隐式特征空间的向量分别为:
![]()
![]()
那么用户u和标的物品v的预测评分为![]() ,真实值与预测值之间的误差为
,真实值与预测值之间的误差为![]() 。如果预测得越准,那么
。如果预测得越准,那么![]() 越小,针对所有用户评分过的(u,v)对,如果我们可以保证这些误差之和尽量小,那么有理由认为我们的预测是精准的。
越小,针对所有用户评分过的(u,v)对,如果我们可以保证这些误差之和尽量小,那么有理由认为我们的预测是精准的。
有了上面的分析,我们就可以将矩阵分解转化为一个机器学习问题。具体地说,我们可以将矩阵分解转化为如下等价的求最小值的最优化问题。SGD和ALS都是损失函数最小化的求解方法。
定义损失函数为:
其中![]() 是超参数,可以通过交叉验证等方式来确定,
是超参数,可以通过交叉验证等方式来确定,![]() 是正则项,避免模型过拟合。
是正则项,避免模型过拟合。
4、随机梯度下降(SGD)
假设用户u对标的物v的评分为![]() ,嵌入k维隐因子空间的向量分别为
,嵌入k维隐因子空间的向量分别为![]() ,我们定义真实评分和预测评分的误差为
,我们定义真实评分和预测评分的误差为![]() ,公式如下:
,公式如下:
![]()
我们可将公式写为如下函数:
![]() 对
对![]() 求偏导数,具体计算如下:
求偏导数,具体计算如下:
有了偏导数,我们沿着导数(梯度)相反的方向更新![]() ,最终我们可以采用如下公式来更新
,最终我们可以采用如下公式来更新![]() 。
。
![]()
![]()
上式中![]() 为步长超参数,也称为学习率(导数前面的系数2可以吸收到参数
为步长超参数,也称为学习率(导数前面的系数2可以吸收到参数![]() 中),取大于零的较小值。
中),取大于零的较小值。![]() 先可以随机取值,通过上述公式不断更新
先可以随机取值,通过上述公式不断更新![]() ,直到收敛到最小值(一般是局部最小值),最终求得所有的
,直到收敛到最小值(一般是局部最小值),最终求得所有的![]() 。
。
SGD方法一般可以快速收敛,但是对于海量数据的情况,单机无法承载这么大的数据量,所以在单机上是无法或者在较短的时间内无法完成上述迭代计算的,这时我们可以采用下面的ALS方法来求解,该方法可以非常容易做分布式拓展。
5、交替最小二乘法(ALS)
ALS算法的原理基本就是名字表达的意思,通过交替优化求得极值。一般过程是先固定Pu,那么下述计算公式就变成了一个关于Qv的二次函数,可以作为最小二乘问题来解决,求出最优的Qv后,固定Qv,再解关于Pu的最小二乘问题,交替进行直到收敛。相比SGD算法,ALS算法有如下两个优势。
(1) 可以并行化处理
(2) 对于隐式特征问题比较合适
计算公式:
简单流程:
(1)随机初始化矩阵P的元素值;
(2)把矩阵P当做已知的,用线性代数的方法求得矩阵Q;
(3)得到了矩阵Q后,把Q当做已知的,用线性代数方法求解矩阵P;
(4)上面过程交替进行,直到误差可以接受为止。
6、显式反馈和隐式反馈
用户给商品评分是个非常简单粗暴的用户行为。在实际的电商网站中,还有大量的用户行为,同样能够间接反映用户的喜好,比如用户的购买记录、搜索关键字,甚至是鼠标的移动。我们将这些间接用户行为称之为隐式反馈(implicit feedback),以区别于评分这样的显式反馈(explicit feedback)。
隐式反馈有以下几个特点:
1.没有负面反馈(negative feedback)。隐式反馈无法判断是否不喜欢,而显式反馈,明显区分是喜欢还是不喜欢。
2.隐式反馈包含大量噪声。
3.显式反馈表现的是用户的偏好,而隐式反馈表现的是用户的置信度。
4.隐式反馈非常难以量化,需要近似评估。
7、加权交替最小二乘法
考虑隐式反馈的矩阵分解,叫做加权交替最小二乘算法:Weighted-ALS。
如果用户对物品无隐式反馈,则认为评分为0。
如果用户对物品有隐式反馈,则认为评分是1,次数作为该评分的置信度。
此时的损失函数如下:
其中,Cui是置信度。Cui=1+a*c,a是调参参数,默认取40,c是次数。
8、考虑时间因素
用户在不同时间和自身状态是不一样的。考虑时间因素,有以下几种做法:
对评分按时间加权,让久远的评分更趋近平均值。
对特殊的日子,如节日,周末等训练对应的隐因子向量
9、考虑历史行为
显式反馈比隐式反馈少得多。在SVD中结合用户的隐式反馈行为和属性(比如性别),这套模型称作SVD++。
加入隐式反馈:用户有过行为的物品集合也配置一个隐因子向量,维度是一样的。把用户操作过的物品隐因子向量加起来,用来表达用户的兴趣偏好。
加入用户属性:全部转换成0-1型,配置隐因子向量同上。
SVD++的损失函数为:
其中,X是隐式反馈向量,Y是用户属性向量。
10、考虑偏置信息
由于每个用户的评分标准不一样,有的比较宽松,有的则比较严格。另外,有些物品可能用户不喜欢,但是用户也不得不买,如大米,白面等。因些需要引入偏置。一个用户对一个物品的评分由多项偏置组成,可对偏置设置权重或其他条件等。