基于Pytorch的强化学习(DQN)之 Multi-agent 基本概念

目录

1. 引言

2. 基本分类

2.1 Fully cooperative

2.2 Fully competitive

2.3 Mixed cooperative&competitive

2.4 Self interested

3. 专业术语

3.1 state and action

3.2 state transtition

3.3 reward and return

3.4 policy network

3.5 state value function

3.6 convergence

---

1. 引言

我们之前所学的所有DQN的内容都基于一个前提：系统中只有一个agent，也就是进行决策的主体只有一个，但是在现实中往往存在需要多个主体同时进行决策的情况，下面我们来学习多智能体(Multi-agent)的一些基础概念。

2. 基本分类

我们人类之前存在合作、竞争等简单的交互关系，agents之间通常也存在以下几种关系。

2.1 Fully cooperative

完全合作关系(fully cooperative)，一些agents可能需要共同完成一个任务，这时它们有一个共同的目标，这便是完全合作，例如汽车制造厂中有许多机器臂对汽车进行不同的操作，最终目标就是组装一辆汽车，因此它们是完全合作关系。

2.2 Fully competitive

完全竞争关系(fully competitive)，有一些agents目标对立，一方胜利另一方就失败，例如两个搏击机器人，它们都想赢下比赛，让对手输掉比赛，这就会出现一个胜利另一个失败的结果，这便是完全竞争。

2.3 Mixed cooperative&competitive

混合关系(mixed cooperative&competitive)，如果在一个系统中同时出现完全合作和完全竞争关系的agents，那么这些agents就是混合关系，例如搏击机器人团队赛，任意一个agent都与和自己一队的agent是完全合作关系，而与其他队的agent是完全竞争关系，所以它们是混合关系。

2.4 Self interested

利己主义(self interested)，有一些agent只关心怎么将自己的利益最大化，而不在乎其他agents怎么变化，我们称这种agent为利己主义者，它们将其他agents看作环境的一部分，最终目标就是最大化自己的利益，例如无人驾驶汽车，agent的目标就是安全快速地到达目的地，其他的无人驾驶汽车在它看来就是环境的一部分，所以它是一个利己主义者。

3. 专业术语

Multi-agent与Single-agent的一些专业术语有些不同。

3.1 state and action

状态和动作与Single-agent的类似，分别用  和  表示观测到的state和第  个agent的action，用  和  表示对应的随机变量。

3.2 state transtition

状态转移也与Single-agent的类似，用概率密度函数 表示，整个系统的状态与所以agent的action都有关，所以含有全部的action。

3.3 reward and return

奖励和回报的概念与Single-agent的类似， 表示第  个agent的reward，考虑两个agents，在两种情况下的reward，我们有

1. 完全合作：
2. 完全竞争：

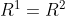
考虑第  个agent，其return的定义为  discounted return为 与Single-agent基本一样。

3.4 policy network

策略网络也和Single-agent的类似，对于第  个agent，其策略网络为  有时候不同agents的参数  是可以交换的，例如两辆同一型号的无人驾驶汽车，但大部分情况下是不可交换的。 

3.5 state value function

状态价值函数与Single-agent的类似，但是状态价值网络需要特别注意，其表达式为 而不是  因为某个agent的当前状态与所有agents的参数有关（你的队员和对手的强弱肯定影响当前局势吧），所以只要有一个agent的参数改变所有的状态价值网络的值都会改变。

3.6 convergence

收敛(convergence)是一个新概念，对于Single-agent，我们称价值函数收敛了，指的是网络找出了一个策略，使得任意改变策略都不会使结果变得更好，而对于Multi-agent，我们称价值函数收敛了，指的是所有agent的策略达到了纳什均衡，即任意一个agent改变策略都不会使自己的结果变得更好，这时候所有agent达到最优。

网络学习的目标就是使结果收敛。但是由于只要有一个agent的参数改变所有的状态价值网络的值都会改变。用Single-agent 那一套往往不能达到收敛，所有我们需要新的方法，下一次介绍。