Pytorch实现高斯混合模型GMM
代码链接:GMM-Pytorch
在数据量很大时,利用GPU进行GMM模型加速
import torch
import numpy as np
from sklearn.covariance import LedoitWolf
def euclidean_metric_np(X, centroids):
X = np.expand_dims(X, 1)
centroids = np.expand_dims(centroids, 0)
dists = (X - centroids) ** 2
dists = np.sum(dists, axis=2)
return dists
def euclidean_metric_gpu(X, centers):
X = X.unsqueeze(1)
centers = centers.unsqueeze(0)
dist = torch.sum((X - centers) ** 2, dim=-1)
return dist
def kmeans_fun_gpu(X, K=10, max_iter=1000, batch_size=8096, tol=1e-40):
N = X.shape[0]
indices = torch.randperm(N)[:K]
init_centers = X[indices]
batchs = N // batch_size
last = 1 if N % batch_size != 0 else 0
choice_cluster = torch.zeros([N]).cuda()
for _ in range(max_iter):
for bn in range(batchs + last):
if bn == batchs and last == 1:
_end = -1
else:
_end = (bn + 1) * batch_size
X_batch = X[bn * batch_size: _end]
dis_batch = euclidean_metric_gpu(X_batch, init_centers)
choice_cluster[bn * batch_size: _end] = torch.argmin(dis_batch, dim=1)
init_centers_pre = init_centers.clone()
for index in range(K):
selected = torch.nonzero(choice_cluster == index).squeeze().cuda()
selected = torch.index_select(X, 0, selected)
init_centers[index] = selected.mean(dim=0)
center_shift = torch.sum(
torch.sqrt(
torch.sum((init_centers - init_centers_pre) ** 2, dim=1)
))
if center_shift < tol:
break
k_mean = init_centers.detach().cpu().numpy()
choice_cluster = choice_cluster.detach().cpu().numpy()
return k_mean, choice_cluster
def _cal_var(X, centers=None, choice_cluster=None, K=10):
D = X.shape[1]
k_var = np.zeros([K, D, D])
eps = np.eye(D) * 1e-10
if centers is not None:
_dist = euclidean_metric_np(X, centers)
choice_cluster = np.argmin(_dist, axis=1)
for k in range(K):
samples = X[k == choice_cluster]
_m = np.mean(samples, axis=0)
k_var[k] = LedoitWolf().fit(samples).covariance_ + eps
return k_var.astype(np.float32)
def mahalanobias_metric_gpu(X, mean, var):
torch.cuda.empty_cache()
dis = torch.zeros([X.shape[0], mean.shape[0]])
for k in range(mean.shape[0]):
_m = mean[k]
_inv = torch.inverse(var[k])
delta = X - _m
temp = torch.mm(delta, _inv)
dis[:, k] = torch.sqrt_(torch.sum(torch.mul(delta, temp), dim=1))
return dis
def check_nan(x):
isnan = torch.isnan(x).int()
loc = isnan.sum()
print(f"any nan: {loc.item()}")
class GMM(object):
def __init__(self, K=5, type='full'):
'''
Initlize GMM
:param K: number of clusters
:param type:
'''
self.K = K
self.type = type
self.eps = 1e-10
self.log2pi = np.log(2 * np.pi)
def _logpdf(self):
'''
X: N x D
mu: K x D
var: K x D x D
alpha: 1 x K
:return: log_prob
'''
log_prob = torch.zeros([self.N, self.K]).cuda()
for k in range(self.K):
mu_k = self.mu[k].unsqueeze(0)
var_k = self.var[k]
var_k_inv = torch.inverse(var_k)
det_var = torch.det(var_k)
delta = self.X - mu_k
temp = torch.mm(delta, var_k_inv)
dist = torch.sum(torch.mul(delta, temp), dim=1)
log_prob_k = -0.5 * (self.D * self.log2pi + torch.log(det_var) + dist) + torch.log(self.alpha[k])
log_prob[:, k] = log_prob_k
return log_prob
def _pdf(self):
'''
X: N x D
mu: K x D
var: K x D x D
alpha: 1 x K
:return:
'''
self.log_prob = self._logpdf()
max_log_prob = -torch.max(self.log_prob, dim=1, keepdim=True)[0]
log_prob = self.log_prob / max_log_prob
self.prob = torch.exp(log_prob)
check_nan(self.prob)
print(self.alpha)
print(f"{torch.max(self.prob)}, {torch.min(self.prob)}")
return self.prob
def _e_step(self):
'''
prob: N x K
'''
self.prob = self._pdf()
prob_sum = torch.sum(self.prob, dim=1, keepdim=True)
self.prob = self.prob / prob_sum
check_nan(self.prob)
return self.prob
def _m_step(self):
'''
X: N x D
mu: K x D
var: K x D x D
alpha: 1 x K
prob: N x K
'''
self.alpha = torch.sum(self.prob, dim=0)
for k in range(self.K):
prob_k = self.prob[:, k].unsqueeze(1)
self.mu[k] = torch.sum(self.X * prob_k, dim=0) / self.alpha[k]
mu_k = self.mu[k].unsqueeze(0)
delta = self.X - mu_k
delta_t = torch.transpose(delta, 0, 1)
delta = delta * prob_k
self.var[k] = torch.mm(delta_t, delta) / self.alpha[k] + self.eps_mat
self.alpha = self.alpha / self.N
def fit(self, X, max_iters=200, tol=1e-60):
'''
fit the X to the GMM model
:param X: N x D
:param max_iters:
:return:
'''
self.X = X
self.N, self.D = X.shape[0], X.shape[1]
self.pi = np.power(np.pi * 2, self.D / 2)
self.eps_mat = torch.eye(self.D).cuda() * self.eps
init_centers, _ = kmeans_fun_gpu(X, K=self.K)
self.mu = torch.from_numpy(init_centers.astype(np.float32)).cuda()
self.var = _cal_var(X.detach().cpu().numpy(), centers=init_centers, K=K)
self.var = torch.from_numpy(self.var).cuda()
self.alpha = torch.ones([self.K, 1]) / self.K
self.alpha = self.alpha.cuda()
log_lh_old = 0
for iter in range(max_iters):
self._e_step()
self._m_step()
log_lh = -torch.sum(self.log_prob)
if iter >= 1 and torch.abs(log_lh - log_lh_old) < tol:
break
log_lh_old = log_lh
print(f"[!!!] Iter-{iter + 1} log likely hood: {log_lh.item():.8f}")
prob = self._e_step()
pred = torch.argmax(prob, dim=1)
return self.mu, pred
class GMM_Batch(object):
def __init__(self, K=5, type='full'):
'''
Initlize GMM
:param K: number of clusters
:param type:
'''
self.K = K
self.type = type
self.eps = 1e-10
self.log2pi = np.log(2 * np.pi)
self.reset_batch_cache()
def reset_batch_cache(self):
self.cache = {"prob": [],
"mu": [[] for _ in range(self.K)],
"var": [[] for _ in range(self.K)],
"alpha": []}
def _logpdf(self, x):
'''
X: N x D
mu: K x D
var: K x D x D
alpha: 1 x K
:return: log_prob
'''
log_prob = torch.zeros([x.shape[0], self.K]).cuda()
for k in range(self.K):
mu_k = self.mu[k].unsqueeze(0)
var_k = self.var[k]
var_k_inv = torch.inverse(var_k)
det_var = torch.det(var_k)
delta = x - mu_k
temp = torch.mm(delta, var_k_inv)
dist = torch.sum(torch.mul(delta, temp), dim=1)
log_prob_k = -0.5 * (self.D * self.log2pi + torch.log(det_var) + dist) + torch.log(self.alpha[k])
log_prob[:, k] = log_prob_k
return log_prob
def _pdf(self, x):
'''
X: N x D
mu: K x D
var: K x D x D
alpha: 1 x K
:return:
'''
self.log_prob = self._logpdf(x)
max_log_prob = -torch.max(self.log_prob, dim=1, keepdim=True)[0]
log_prob = self.log_prob / max_log_prob
self.prob = torch.exp(log_prob)
return self.prob
def _e_step(self, x):
'''
prob: N x K
'''
self.prob = self._pdf(x)
prob_sum = torch.sum(self.prob, dim=1, keepdim=True) + self.eps
self.prob = self.prob / prob_sum
check_nan(self.prob)
self.cache['prob'].append(self.prob)
return self.prob
def _m_step(self, x):
'''
X: N x D
mu: K x D
var: K x D x D
alpha: 1 x K
prob: N x K
'''
self.alpha = torch.sum(self.prob, dim=0)
for k in range(self.K):
prob_k = self.prob[:, k].unsqueeze(1)
self.cache['mu'][k].append(torch.sum(x * prob_k, dim=0).unsqueeze(0))
mu_k = self.mu[k].unsqueeze(0)
delta = x - mu_k
delta_t = torch.transpose(delta, 0, 1)
delta = delta * prob_k
self.cache['var'][k].append(torch.mm(delta_t, delta).unsqueeze(0))
self.cache['alpha'].append(self.alpha.unsqueeze(0))
def fit(self, X, batch_size=1024, max_iters=200, tol=1e-60):
'''
fit the X to the GMM model
:param X: N x D
:param max_iters:
:return:
'''
self.N, self.D = X.shape[0], X.shape[1]
self.pi = np.power(np.pi * 2, self.D / 2)
self.eps_mat = torch.eye(self.D).cuda() * self.eps
init_centers, _ = kmeans_fun_gpu(X, K=self.K)
self.mu = torch.from_numpy(init_centers.astype(np.float32)).cuda()
self.var = _cal_var(X.detach().cpu().numpy(), centers=init_centers, K=K)
self.var = torch.from_numpy(self.var).cuda()
self.alpha = torch.ones([self.K, 1]) / self.K
self.alpha = self.alpha.cuda()
batchs = self.N // batch_size
last = 1 if self.N % batch_size != 0 else 0
log_lh_old = 0
for iter in range(max_iters):
for bn in range(batchs + last):
if bn == batchs and last == 1:
_end = -1
else:
_end = (bn + 1) * batch_size
X_batch = X[bn * batch_size: _end]
self._e_step(X_batch)
self._m_step(X_batch)
self.alpha = torch.cat(self.cache['alpha'], dim=0)
self.alpha = torch.sum(self.alpha, dim=0)
for k in range(self.K):
mu_k = torch.cat(self.cache['mu'][k], dim=0)
self.mu[k] = torch.sum(mu_k, dim=0) / self.alpha[k]
var_k = torch.cat(self.cache['var'][k], dim=0)
self.var[k] = torch.sum(var_k, dim=0) / self.alpha[k] + self.eps_mat
self.alpha = self.alpha / self.N
prob = torch.cat(self.cache['prob'], dim=0)
log_lh = -torch.sum(prob.log())
self.reset_batch_cache()
if iter >= 1 and torch.abs(log_lh - log_lh_old) < tol:
break
log_lh_old = log_lh
print(f"[!!!] Iter-{iter + 1} log likely hood: {log_lh.item():.8f}")
pred = torch.argmax(prob, dim=1)
return self.mu, pred
if __name__ == "__main__":
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import time
n = 1000000
n1 = 5000
K = 5
data, label = make_blobs(n_samples=n, n_features=512, centers=K)
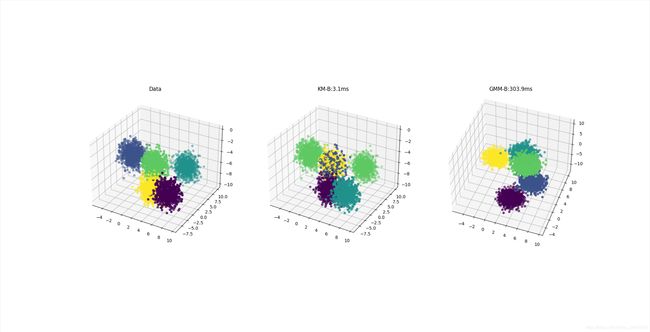
fig = plt.figure(facecolor='white')
ax = fig.add_subplot(1, 3, 1, projection='3d', facecolor='white')
ax.scatter(data[:n1, 0], data[:n1, 1], data[:n1, 2], c=label[:n1])
ax.set_title("Data")
X = torch.from_numpy(data.astype(np.float32)).cuda()
st = time.time()
mean, pre_label = kmeans_fun_gpu(X, K, max_iter=1000)
et = time.time()
print(f"KMeans-Batch-pytorch fitting time: {(et - st):.3f}ms")
ax = fig.add_subplot(1, 3, 2, projection='3d', facecolor='white')
ax.scatter(data[:n1, 0], data[:n1, 1], data[:n1, 2], c=pre_label[:n1])
ax.set_title(f"KM-B:{(et - st):.1f}ms")
st = time.time()
gmm = GMM_Batch(K=K)
_, pre_label = gmm.fit(X, batch_size=100000, max_iters=200)
pre_label = pre_label.detach().cpu().numpy()
print(gmm.alpha)
et = time.time()
print(f"GMM-Batch-pytorch fitting time: {(et - st):.3f}ms")
ax = fig.add_subplot(1, 3, 3, projection='3d', facecolor='white')
ax.scatter(data[:n1, 0], data[:n1, 10], data[:n1, 20], c=pre_label[:n1])
ax.set_title(f"GMM-B:{(et - st):.1f}ms")
plt.show()