Physics-Informed DeepONet for Nonlinear PDEs：一种学习无穷维空间映射的方法

Physics-Informed DeepONet for Nonlinear PDEs：一种学习无穷维空间映射的方法

  深度学习在CV上大获成功之后，也开始在更多的领域攻城掠地，不断地挑战各种传统方法。神经网络展现出了强大的魔力，能够克服传统算法的运行速度较慢的困难，但是也确实相应的理论分析和长期的实践验证。

简介

  一般而言，传统的偏微分方程求解器主要依赖有限插法法、有限元方法和伪谱法等，二分类的话就是有网格和无网格方法。以迭代的方法近似求解偏微分方程，这类传统方法能够严格地给出误差上下界，精确给出算法复杂度。这些方法已经相当成熟了，大部分比较实用的方法已经被集成在商业求解软件中了（这里插一句，现在国防工业中大量需要懂有限元方法的人才）。传统求解器的主要缺点就是计算量特别大，只要有参数发生变化，就需要进行重复且巨量的计算，速度很难满足实时计算的要求。

  深度学习求解微分方程其实是伴随着神经网路的发展，1995年的时候就有人证明了对于任意的光滑、局部Lipschitz的常微分方程，都存在一个神经网络以任意逼近精度对该方程进行逼近。DeepONet就是延续了这个思路对连续非线性算子进行逼近。

  这里还介绍一下什么是Physics Informed，这个概念我的理解就是将物理先验融合到神经网络架构中去，通俗一点来讲就是将偏微分方程的约束加入到loss项中来。原始版本的DeepONet有个问题就是，数据驱动的方式不一定能够满足偏微分方程的约束。但是Physics Informed方式也存在问题，就是在loss项中，偏微分方程的约束会使边界条件及初始条件的约束很难被满足，也就是所说的违反因果性了。初始条件和边界条件是主导偏微分方程的解，但是Physics Informed往往会使偏微分方程的约束被隐形满足，但是突破了初始条件和边界条件的约束，违反了因果性这一本质要求。关于Physics- informed machine learning这个主题可以参考陆路博士的综述

Karniadakis, George Em, et al. "Physics-informed machine learning." Nature Reviews Physics 3.6 (2021): 422-440.

  我这里也给出两个比较重要的图。这张图表示网络偏置的产生原因

这张图代表了数据与物理先验的关系，也即当物理先验较复杂时，数据的产生会比较困难，需要协调数据驱动与物理先验之间的关系。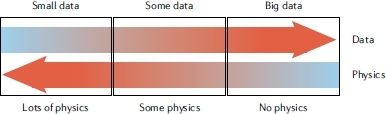

主要思路和方法

  先总结一下目前对于深度学习求解PDE的两种主流思路：

1. 直接学习无穷维空间之间的映射，也就是说直接将初始条件映射到对应的时空条件下，也就说我本质上是用深度神经网络学习了一个无穷维映射算子，这种方法的好处就是非常直接暴力，但是如果训练样本不够多的话，对于处于分布之外的解泛华性能是存疑的。这种思路的主要代表性工作就是DeepONet和FNO（傅里叶算子神经网络）；
2. 自回归方法，类似于传统方法，使用迭代的思路进行求解，在一个较小的时间间隔内使用神经网络学习到增量变化，然后在整个时空区域进行迭代推进，最终得到指定时空条件下的解，这一类方法的泛化性能比较好，但是计算量相对比较大，主要原因是迭代的方法需要大量的重复计算。里面有一个问题，就是积累的误差如何进行修正，这类方法的代表性工作就是基于GNN（图神经网络）求解器；

  这里也给出我目前调研到的主要方法

1. 深度神经网络，也即本文要讨论的DeepONet及其衍生的一些系列算法，这类算法就比较直接好理解，也是一部分研究者主要研究的方法;
2. 图神经网络，图神经网络也是借鉴了传统有限元方法，使用离散化的方法将空间域建模为图网络，结合神经网络进行节点更新，也就是求解，目前来说是消息传递机制、傅里叶算子神经网络比较霍；
3. 多尺度神经网络，这算是深度神经网络的一个分支，主要想要解决的是长时间尺度和大空间域的求解问题。

Physics-Informed DeepONet

  这一部分给出主要技术细节，这一块其实是最简单的，下面给出主要的两篇参考文献：

Lu, Lu, et al. "Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators." Nature Machine Intelligence 3.3 (2021): 218-229.
Wang, Sifan, Hanwen Wang, and Paris Perdikaris. "Learning the solution operator of parametric partial differential equations with physics-informed DeepONets." Science advances 7.40 (2021): eabi8605.

  DeepONet的主要思路就下面两个非线性算子理论：
  定理一：假定\(\sigma\)是一个非多项式函数，\(X\)是一个Banach空间，\(K_{1} \subset X\)，\(K_{2} \subset \mathbb{R}^{d}\)分别是\(X\)和\(\mathbb{R}^{d}\)上的紧集，\(V\)是\(C\left(K_{1}\right)\)上的紧集，\(G\)是一个将\(V\)映射到\(C\left(K_{2}\right)\)的连续非线性算子。那么对于任意\( \epsilon > 0\)，存在正整数\(m\)、\(p\)和\(n\)，常数\(c_i^k\)、\(\xi _{ij}^{k}\)、\(\theta _{i}^{k}\)、\(\zeta _k\in \mathbb{R}\)、\(w_k \in \mathbb{R} ^d\)、\(x_j\in K_1\)、\(i=1,...,n \)，\(k=1,...,p\)，\(j=1,...,m\)使得

$$ \left|G(u)(y)-\sum_{k=1}^{p} \underbrace{\sum_{i=1}^{n} c_{i}^{k} \sigma\left(\sum_{j=1}^{m} \xi_{i j}^{k} u\left(x_{j}\right)+\theta_{i}^{k}\right)}_{\text {branch }} \underbrace{\sigma\left(w_{k} \cdot y+\zeta_{k}\right)}_{\text {trunk }} \right|<\epsilon $$

对于任意\(u \in V\) and \(y \in K_{2}\)成立。\(C(K)\)是所有定义在\(K\)上的所有连续函数的Banach空间，其范数为\(|f|_{C(K)}=\max _{x \in \mathbb{K}}|f(x)|^{\prime}\)。

  定理二：假定\(X\)是一个Banach空间，\(K_{1} \subset X\)，\(K_{2} \subset \mathbb{R}^{d}\)分别是\(X\)和\(\mathbb{R}^{d}\)上的紧集，\(V\)是\(C\left(K_{1}\right)\)上的紧集，\(G\)是一个将\(V\)映射到\(C\left(K_{2}\right)\)的连续非线性算子。那么对于任意\( \epsilon > 0\)，存在两个正整数\(m\)和\(p\)，以及连续向量函数\( \mathbf{g}:\mathbb{R} ^m \Rightarrow \mathbb{R} ^p \)、\( \mathbf{f}:\mathbb{R} ^d \Rightarrow\mathbb{R} ^p \)和\( x_1,x_2,...,x_m \in K_1\)使得

$$ \left|G(u)(y)-\langle\underbrace{\mathbf{g}\left(u\left(x_{1}\right), u\left(x_{2}\right), \cdots, u\left(x_{m}\right)\right)}_{\text {branch }}, \underbrace{\mathbf{f}(y)}_{\text {trunk }}\rangle\right|<\epsilon $$

对于任意\(u \in V\)和\(y \in K_{2}\)成立，其中\(\langle\cdot, \cdot\rangle\)是向量内积符号。此外，函数\(\mathbf{g}\)和\(\mathbf{f}\)可以选择为满足经典通用函数逼近定理的不同类别的神经网络，例如（堆叠/非堆叠）全连接神经网络、残差神经网络和卷积神经网络。

  通过这两个逼近定理，其实神经网络的架构已经呼之欲出了，\(\sigma\)、\(\mathbf{g}\)和\(\mathbf{f}\)都可以看成一个神经网络，最简单的就是多层感知机(MLP)。下面我们就给出两种网络结构（堆叠和非堆叠）：

堆叠和非堆叠其实差异不大，非堆叠的相当于堆叠的网络共享相同的参数。当然了，这里其实有一点是非常疑惑性的，就是\(x_1,x_2,...,x_m \)代表的是空间位置，那么\(y\)也代表的是空间位置，那两者应该是等价的，为什么作者不用统一变量来进行表示，这里就是作者挖的第一个坑。我也不知道作者为啥不在这里明确表示，其实这里的\( y:\mathbb{R} ^m\)其实可以看作是\( y=\left[ x,t \right] \)，这里的\( x\)就和图上的\(x_1,x_2,...,x_m \)对应上了。时间\( t\)没有显示地表现出来，但是在实际操作中\(t\)是被包含在\( y:\mathbb{R} ^m\)中被Trunk Net显式编码，想明白这一点整个DeepONet就能很快弄明白了。

  下面我们介绍Physics Informed DeepONet的损失函数

$$ \mathcal{L} (\boldsymbol{\theta })=\lambda _{ic}\mathcal{L} _{ic}(\boldsymbol{\theta })+\lambda _{bc}\mathcal{L} _{bc}(\boldsymbol{\theta })+\lambda _r\mathcal{L} _r(\boldsymbol{\theta })+\lambda _g\mathcal{L} _g(\boldsymbol{\theta }) $$

各项为

$$ \mathcal{L} _{ic}(\boldsymbol{\theta })=\frac{1}{N_{ic}}\sum_{i=1}^{N_{ic}}{\left| \boldsymbol{u}_{\boldsymbol{\theta }}\left( 0,\boldsymbol{x}_{ic}^{i} \right) -\boldsymbol{g}\left( \boldsymbol{x}_{ic}^{i} \right) \right|^2} \\ \mathcal{L} _{bc}(\boldsymbol{\theta })=\frac{1}{N_{bc}}\sum_{i=1}^{N_{bc}}{\left| \mathcal{B} \left[ \boldsymbol{u}_{\boldsymbol{\theta }} \right] \left( t_{bc}^{i},\boldsymbol{x}_{bc}^{i} \right) \right|^2} \\ \mathcal{L} _r(\boldsymbol{\theta })=\frac{1}{N_r}\sum_{i=1}^{N_r}{\left| \frac{\partial \boldsymbol{u}_{\boldsymbol{\theta }}}{\partial t}\left( t_{r}^{i},\boldsymbol{x}_{r}^{i} \right) +\mathcal{N} \left[ \boldsymbol{u}_{\boldsymbol{\theta }} \right] \left( t_{r}^{i},\boldsymbol{x}_{r}^{i} \right) \right|^2} \\ \mathcal{L} _g(\boldsymbol{\theta })=\frac{1}{PN_g}\sum_{j=1}^P{\sum_{i=1}^{N_g}{\left| \boldsymbol{u}_{\boldsymbol{\theta }}\left( t_{r}^{j},\boldsymbol{x}_{g}^{i} \right) -\boldsymbol{u}_g\left( t_{r}^{j},\boldsymbol{x}_{g}^{i} \right) \right|^2}} $$

这里\(\mathcal{L} _{ic}(\boldsymbol{\theta })\)代表了初始条件的损失函数，也就是相当于约束神经网络一定要满足初始条件，这一项的计算直接将\(t = t_0\)即可；\(\mathcal{L} _{bc}(\boldsymbol{\theta })\)代表了边界条件的损失函数，也就是强迫神经网络的满足边界约束，这个也可以轻松计算；\(\mathcal{L} _{r}(\boldsymbol{\theta })\)这一项及时Physics Informed损失项，也就是让神经网络的解能够满足偏微分方程约束，这一项的引入也开始了Physics-informed neural networks (PINNs)的研究；\(\mathcal{L} _{g}(\boldsymbol{\theta })\)代表了神经网络预测的解和真实值之间的差值。这四项基本就是这一方面研究常用的四项，通常来说前三项都会使用，第四项根据实际情况引入。\(\lambda _{ic}\)、\(\lambda _{bc}\)、\(\lambda _{r}\)和\(\lambda _{g}\)是预先设定的系数，一般都取为1，也就意味着是超参数。需要指出的是，损失函数的计算依赖对空间域上的采样，如何采样也会影响神经网络的优化，一般都是均匀采样或者随机采样，最近也有人引入Attention机制自学习感兴趣区域。

这里神经网络的优化方式使用梯度下降，也即

$$ \boldsymbol{\theta }_{k+1}=\boldsymbol{\theta }_k-\eta \nabla _{\boldsymbol{\theta }}\mathcal{L} (\boldsymbol{\theta }) $$

\( \eta\)是学习律，这个和深度学习里设定学习律基本一致。这里也牵涉到激活函数的选取，一般都是使用DeepXDE自带的自适应激活函数，ReLU由于二阶以上导不存在，一般不使用。具体的优化方式可以是mini-batch SGD（随即梯度下降）。

  这里需要提到一个问题，也就是自动微分机制。为什么要用自动微分机制，很多人可能回认为通过数值差分的方法就能计算各阶偏导数，由于偏微分方程的偏导数阶数通常非常高，这样一次次地迭代计算高阶偏导数项会导致比较大的误差。此外，需要指出的是，实际中数据都是存在噪声的，噪声数据是很难用数值差分的方式计算得到的。当然了，目前也有一些方法是结合数值方法和自动微分机制。Tensorflow和Pytorch都没有提供提供偏微分方程的高阶倒数计算方法，这里推荐使用DeepXDE包（也是由DeepONet作者陆路博士开发的）。使用自动微分机制可以快速计算损失函数及其导数。

  到这里基本Physics Informed DeepONet所有细节就介绍完了，不得不感叹这个方法的简洁与高效。实验部分这里就不赘述，如果有需要可以详细读一下相关论文。

思考与展望

  关于DeepONet的数学分析和拓展可以分别参考下面两篇文章：

Lanthaler, Samuel, Siddhartha Mishra, and George E. Karniadakis. "Error estimates for DeepONets: A deep learning framework in infinite dimensions." Transactions of Mathematics and Its Applications 6.1 (2022): tnac001.
Lu, Lu, et al. "A comprehensive and fair comparison of two neural operators (with practical extensions) based on fair data." Computer Methods in Applied Mechanics and Engineering 393 (2022): 114778.

  综合我最近读的一些论文，我给出一些有潜力的研究方法：

1. Attention机制:该方法主要解决空间域的采样方法，self-Attention能够较好地解决这一问题已经有人开始探索这个领域了；

   Kissas, Georgios, et al. "Learning Operators with Coupled Attention." arXiv preprint arXiv:2201.01032 (2022).

2. 图神经网络：该方法能够和传统方法结合，用神经网络替代传统的迭代计算方法；
3. Meta-Learning方法：偏微分方程中有部分参数在不同应用场景下会发生一定范围的变化，我们可以利用已有的结果快速对新参数泛化，这部分也有人开始研究；
4. 长时间尺度和多物理域问题。