第十届蓝桥杯省赛B组部分题解

一直都在各大论坛看别人的帖子，想着什么时候能自己也写一写自己的一些随笔和学习心得。拖了好久今天终于动笔了，本人蒟蒻一枚。。还请各位多多指教*^^_^*

1. A组队
2. B年号字串
3. C数列求值
4. D数的分解
5. E迷宫
6. F特别数的和
7. G完全二叉树的权值

试题 A: 组队

作为篮球队教练，你需要从以下名单中选出 1 号位至 5 号位各一名球员，
组成球队的首发阵容,每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1号位至 5 号位的评分之和最大可能是多少？

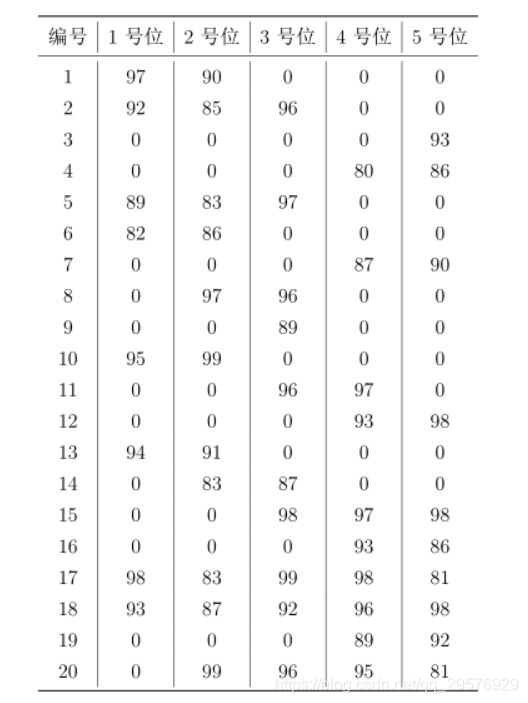
填空题直接选即可，注意别选重复了。
答案：490

试题 B: 年号字串

小明用字母 A 对应数字 1，B 对应 2，以此类推，用 Z 对应 26。对于 27以上的数字，小明用两位或更长位的字符串来对应，例如 AA 对应 27，AB 对应 28，AZ 对应 52，LQ 对应 329。
请问 2019 对应的字符串是什么？

求2019的26进制表示，分别用字母A~Z，手算也很快，代码如下。
（当数被26整除时，应回退一位表示为**Z）

#include 
using namespace std;
int main (){
   stack<int>s;
   int n;
   cin >> n;
   while (n != 0){
     s.push(n % 26);
      n = n / 26;
  }
  while (!s.empty()){
  cout << (char)(s.top() + 64) << endl;
  s.pop();
 }
 return 0;
}

答案：BYQ

试题 C: 数列求值

给定数列 1, 1, 1, 3, 5, 9, 17, …，从第 4 项开始，每项都是前 3 项的和。求
第 20190324 项的最后 4 位数字。

类似于斐波那契数列的递推公式，要注意保留后四位，一边取模一边求和，否则会溢出。代码如下

#include 
using namespace std;
int main (){
   int a = 1, b = 1, c = 1,d;
   for (int i = 4;i <= 20190324;i++){
    d = (a % 10000 + b % 10000 + c % 10000) % 10000;
    a = b;
    b = c;
    c = d;
   }
   cout << d << endl;
   return 0;
}

答案：4659

试题 D: 数的分解

把 2019 分解成 3 个各不相同的正整数之和，并且要求每个正整数都不包
含数字 2 和 4，一共有多少种不同的分解方法？
注意交换 3 个整数的顺序被视为同一种方法，例如 1000+1001+18 和
1001+1000+18 被视为同一种。

比赛时不知道怎么想的，一直在考虑如何去重，选用错误的去重方法所以漏了好多合法解。。。其实可以直接暴力，计算结果除以3个数的全排列数即最终答案，虽然跑的时间有点恐怖。。。
好可惜：（
代码如下

#include 
using namespace std;
bool ok(int x){
    while (x != 0){
    int temp = x % 10;
    x /= 10;
    if (temp == 2 || temp == 4){
     return false;
    }
  }
   return true;
}
int main (){
   int ans = 0;
   for (int i = 1;i <= 1999;i++){
     for (int j = 1;j <= 1999;j++){
       for (int k = 1;k <= 1999;k++){
         if (i != j && j != k && k != i && ok(i) && ok(j) && ok(k) && i + j + k == 2019){
               ans++;
         }
      }
    }
  }
 cout << ans / 6 << endl;
 return 0;
}

答案：40785

试题 E: 迷宫

下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可
以通行的地方。
010000
000100
001001
110000
迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这
个它的上、下、左、右四个方向之一。
对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫，一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。对于下面这个更复杂的迷宫（30 行 50 列） ，请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。
请注意在字典序中D

找到最优路径，很明显的BFS。可惜当时对BFS练的少，一直纠结于如何输出路径上。。。还是太菜太菜太菜。赛后听朋友说可以直接给结构体加个string参数，在BFS的时候直接记录路径即可。

#include 
using namespace std;
int dir[4][2] = {{1, 0},{0, -1},{0, 1},{-1, 0}};
char mp[100][100];
bool vis[100][100];
char mk[4] = {'D','L','R','U'};
struct node{
 int x, y, step;
 string path;
 node(int xx, int yy, int sstep, string ppath){
  x = xx;
  y = yy;
  step = sstep;
  path = ppath;
 }
};
int n, m;
bool in(int x, int y){
  return x >= 0 && x < n && y >= 0 && y < m;
}
void bfs(int x, int y){
 queue<node>q;
 q.push(node(x, y, 0, ""));
 vis[x][y] = true;
 while (!q.empty()){
  node now = q.front();
  q.pop();
  if (now.x == n - 1 && now.y == m - 1){
   cout << now.path << endl;
   break;
  }
  
  for (int i = 0;i < 4;i++){
   int tx = now.x + dir[i][0];
   int ty = now.y + dir[i][1];
   if (in(tx, ty) && !vis[tx][ty] && mp[tx][ty] == '0'){
    q.push(node(tx, ty, now.step + 1, now.path + mk[i]));
    vis[tx][ty] = true;
   }
  }
 }
}
int main (){
   cin >> n >> m;
   for (int i = 0;i < n;i++){
    for (int j = 0;j < m;j++){
      cin >> mp[i][j];
     }
   }
   bfs(0, 0);
   return 0;
}

答案：DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR

试题 F: 特别数的和

【问题描述】
小明对数位中含有 2、0、1、9 的数字很感兴趣（不包括前导 0） ，在 1 到
40 中这样的数包括 1、2、9、10 至 32、39 和 40，共 28 个，他们的和是 574。
请问，在 1 到 n 中，所有这样的数的和是多少？
【输入格式】
输入一行包含两个整数 n。
【输出格式】
输出一行，包含一个整数，表示满足条件的数的和。
【样例输入】
40
【样例输出】
574
【评测用例规模与约定】
对于 20% 的评测用例，1 ≤ n ≤ 10。
对于 50% 的评测用例，1 ≤ n ≤ 100。
对于 80% 的评测用例，1 ≤ n ≤ 1000。
对于所有评测用例，1 ≤ n ≤ 10000。

找出数字1~n中数位包含2，0 ，1，9的数字，暴力即可。

代码：

#include 
using namespace std;
bool ok(int x){
 while (x != 0){
  int temp = x % 10;
  x /= 10;
  if (temp ==  0 || temp == 2 || temp == 1 || temp == 9){
   return true;
   break;
  }
 }
 return false;
}
int main (){
 int n;
 cin >> n;
 int sum = 0;
 for (int i = 1;i <= n;i++){
  if (ok(i)){
   sum += i;
  }
 }
 cout << sum << endl;
 return 0;
}

试题 G: 完全二叉树的权值

【问题描述】
给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从
上到下、从左到右的顺序依次是 A 1 , A 2 , ··· A N ，如下图所示：
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点
权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。
注：根的深度是 1。
【输入格式】
第一行包含一个整数 N。
第二行包含 N 个整数 A 1 , A 2 , ··· A N 。
【输出格式】
输出一个整数代表答案。
【样例输入】
7
1 6 5 4 3 2 1
【样例输出】
2
【评测用例规模与约定】
对于所有评测用例，1 ≤ N ≤ 100000，?100000 ≤ A i ≤ 100000。

完全二叉树的第 i 层的最大节点数为 2^(i-1) 个，完全二叉树的节点总数和深度的关系为深度为 n 的完全二叉树最多拥有 2^n - 1 个节点。可以求出n个结点的树的深度，然后按深度把每层的权值相加并求最大即可。

题目考察二叉树的性质，应该也不算很难，当时因为没有学过系统的学过数据结构，感觉有点难所以就选择了放弃。。。其实二叉树的性质就那么几个，花点时间也是可以做的。

代码

#include 
using namespace std;
int a[100009];
int b[10000];
int main (){
 int n;
 cin >> n;
 for (int i = 0;i < n;i++){
  cin >> a[i];
 }
 b[1] = a[0];
 int k;
 for (int i = 0;i < 10000;i++){
  if (1 << i == n + 1){
   k = i;
   break;
  }
 }
 
 for (int i = 2;i <= k;i++){
  int cent = 1 << i - 1;
  for (int j = cent;j < (cent + 1 << (i - 1));j++){
   b[i] += a[j];
  }
 }
 int max = -0x3f3f3f;
 for (int i = 0;i < k;i++){
  if (b[i] >= max){
   max = b[i];
  }
 }
 
 for (int i = 0;i < k;i++){
  if (b[i] == max){
   cout << i << endl;
   break;
  }
 }
 return 0;
}

_ 今天就先写到这里，剩下的3个题后续补上。现在回过头来想想，好多东西并没有想象中那么难，平时还是得多做做题（逃。
emmmm总的来说还是so vegetable，没有预想的成绩。今后慢慢来吧。。_

以上只是个人思路，不保证正确性，如果博客中有什么不正确的地方，请多多指点。谢谢观看QAQ~