Opencv学习笔记(六)图像金字塔
大纲
- 一、高斯金字塔
-
- 1.数学原理讲解
-
- i.下采样
- ii.上采样
- 2.Sift尺度中的高斯金字塔
- 3.差分金字塔
- 4.高斯金字塔在图像缩放中的应用
- 二、拉普拉斯金字塔
-
- 1.数学原理
一、高斯金字塔
1.数学原理讲解
标准意义上的高斯金字塔指的是不同分辨率的同一张图像所组成的图像结构,金字塔从上往下生成,图片的分辨率不断增大,称作上采样;金字塔从下往上生成,图片的分辨率不断减下,称作下采样(从下往上依次为 G 0 、 G 1 、 G 2 . . . . G N G_0、G_1、G_2....G_N G0、G1、G2....GN层)。
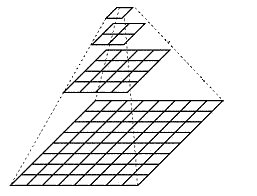
i.下采样
下采样是对图像进行缩小的过程,期间图像分辨率不断降低,图片的信息在不断丢失,从下一层往上一层生成的过程分为两步
(一)对底层图像进行高斯卷积,通常选用归一化5×5高斯卷积和进行卷积;
(二)删除所有的偶数行和偶数列,图片大小变为原来1/4;
示例代码如下:
int main()
{
Mat srcImg = imread("E:\\material\\assassin.jpeg");
if (srcImg.empty())
{
cout << "图片读取错误";
return -1;
}
imshow("原始图片", srcImg);
vector<Mat> tempImg;
tempImg.push_back(srcImg);
for (int k = 0;k < 4;k++)
{
Mat tempimg= Mat::zeros(cvFloor(tempImg[k].size[0] /2), cvFloor(tempImg[k].size[1] / 2), srcImg.type());
tempImg.push_back(tempimg);
Mat dstImg = Mat(tempImg[k].size(), tempImg[k].type());
GaussianBlur(tempImg[k], dstImg, Size(5, 5), 0, 0);
for (int i = 0;i < tempImg[k+1].size[0];i++)
{
for (int j = 0;j < tempImg[k+1].size[1];j++)
{
tempImg[k+1].at<Vec3b>(i, j) = dstImg.at<Vec3b>(2 * i, 2 * j);
}
}
char windowname[20];
sprintf_s(windowname, "%s%d%s", "第", k+1, "次缩小.png");
imshow(windowname, tempImg[k+1]);
imwrite(windowname , tempImg[k + 1]);
}
while ((char)waitKey(0) != 'q');
return 0;
}
ii.上采样
下采样是对图像进行放大的过程,期间图像的分辨率不断升高,从上一层到下一层的生成过程分为两步:
(一)将图像在行和列上扩大两倍,隔一补一,新增的行和列用0来填充;
(二)使用与“下采样”相同的卷积核乘以4与放大后的图像进行卷积;
示例代码如下:
int main()
{
Mat srcImg = imread("第4次缩小.png");
if (srcImg.empty())
{
cout << "图片读取错误";
return -1;
}
imshow("原始图片", srcImg);
vector<Mat> tempImg;
tempImg.push_back(srcImg);
for (int k = 0;k < 4;k++)
{
Mat tempimg= Mat::zeros(cvFloor(tempImg[k].size[0]*2), cvFloor(tempImg[k].size[1]*2), srcImg.type());
for (int i = 0;i < tempImg[k].size[0];i++)
{
for (int j = 0;j < tempImg[k].size[1];j++)
{
tempimg.at<Vec3b>(2*i, 2*j) = tempImg[k].at<Vec3b>(i, j);
}
}
Mat dstImg = Mat(tempimg.size(), tempimg.type());
GaussianBlur(tempimg, dstImg, Size(5, 5), 0, 0);
dstImg = 4 * dstImg;
tempImg.push_back(dstImg);
char windowname[20];
sprintf_s(windowname, "%s%d%s", "第", k+1, "次放大.png");
imshow(windowname, tempImg[k+1]);
imwrite(windowname , tempImg[k + 1]);
}
while ((char)waitKey(0) != 'q');
return 0;
}
实验结果:
![]()



需要注意的是下采样和上采样并不是互逆的两个过程,这一点可以从上采样之后的图片与下采样中相应图片的对比发现,因为下采样过程中消失了很多的图片信息。
2.Sift尺度中的高斯金字塔
高斯金字塔在sift(尺度不变特征变换)中的概念和前面的介绍有所不同,但其原理基本一致。在sift中,高斯金字塔分为组和层,每一组金字塔包含若干层。这一金字塔结构如下:
(一) 将原图扩大1倍之后作为第一组的第一层,将第一组第一层经高斯卷积之后得到第二层,高斯卷积函数(其中 σ \sigma σ取1.6):
G ( x , y ) = 1 2 π σ 2 e − ( x − x 0 ) 2 − ( y − y 0 ) 2 2 σ 2 G(x,y)={{1}\over{2\pi\sigma^2}}e^{-{{(x-x_0)^2-(y-y_0)^2}\over{2\sigma^2}}} G(x,y)=2πσ21e−2σ2(x−x0)2−(y−y0)2
(二) 对第一组第一层进行高斯卷积,但高斯卷积函数中的 σ \sigma σ要乘以一个系数k,所得结果作为第一组第二层;
(三) 后续重复步骤二对上一层进行高斯卷积,高斯卷积中 σ \sigma σ继续乘以系数k,最终得到第一组的N层图像,每一层尺寸都是原图的2倍,且都是对前一层进行高斯卷积得到,只是参数 σ \sigma σ不同,依次为 σ \sigma σ, k σ k\sigma kσ、 k 2 σ k^2\sigma k2σ… k N − 2 σ k^{N-2}\sigma kN−2σ.
(四) 将第一组的倒数第三层 进行比例因子为2的降采样,得到尺寸为其1/4的图片作为第二组的第一层,重复步骤(一)~(三)得到第二组N层;
(五) 重复步骤(四)得到M组N层高斯金字塔;
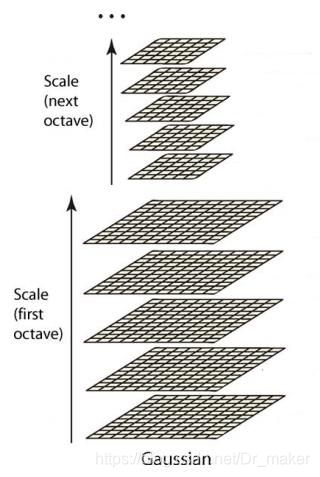
3.差分金字塔
而得到了sift中的高斯金字塔有什么用呢?这就需要引入差分金字塔的概念了,差分金字塔是在高斯金字塔的基础上构建的,对应M组N层高斯金字塔有M组N-1层差分金字塔,其每组第一层都是由高斯金字塔中相应组第二层减第一层得到;每组第二层由高斯金字塔中相应组第三层减第二层得到,后续同理。对所得所用差分金字塔图像进行归一化,我们可以获取在任何尺度变换及模糊程度下图片仍旧保持不变的特征,这就是我们想要获取的稳定特征。
4.高斯金字塔在图像缩放中的应用
Opencv给出了相应的下采样和上采样函数供我们对图像进行缩放。
下采样函数pyrDown()函数原型:
pyrDown( InputArray src, OutputArray dst,const Size& dstsize = Size(),
int borderType = BORDER_DEFAULT );
第一、二个参数为输入输出图像,二者应该有相同的尺寸及类型;
第三个参数为希望输出图像变成的尺寸,有默认值Size ((src.cols+1)/2,(src.rows+1)/2),如果是自行设定的话,需要满足:
∣ d s t s i z e . w i d t h − s r c . c o l s ∣ ≤ 2 |dstsize.width-src.cols|\le2 ∣dstsize.width−src.cols∣≤2
∣ d s t s i z e . h e i g h t − s r c . r o w s ∣ ≤ 2 |dstsize.height-src.rows|\le2 ∣dstsize.height−src.rows∣≤2
猜测这是针对与原图长或者宽为奇数时,可以在下采样第二步选择少去除一行(列)或者多去除一行(列),例如原图为长为51时,输出图像长度可选25或者26;
第四个参数为边界填充类型;
上采样函数pyrUp函数原型:
pyrUp( InputArray src, OutputArray dst,const Size& dstsize = Size(),
int borderType = BORDER_DEFAULT );
除第三个参数外与pyrDown()没有区别,pyrUp第三个参数也为输出图像尺寸,默认Size (src.cols*2,src.rows*2),如果自行设定,需要满足:
∣ d s t s i z e . w i d t h − s r c . c o l s ∗ 2 ∣ ≤ ( d s t s i z e . w i d t h m o d 2 ) |dstsize.width-src.cols*2|\le(dstsize.width\ mod \ 2) ∣dstsize.width−src.cols∗2∣≤(dstsize.width mod 2)
∣ d s t s i z e . h e i g h t − s r c . r o w s ∗ 2 ∣ ≤ ( d s t s i z e . h e i g h t m o d 2 ) |dstsize.height-src.rows*2|\le(dstsize.height\ mod \ 2) ∣dstsize.height−src.rows∗2∣≤(dstsize.height mod 2)
猜测是为了适应不同的插值方式,像是原图长为10时,可以选择第10行后面不插也可以选择插,这样输出就会是20或者21;
二、拉普拉斯金字塔
1.数学原理
拉普拉斯金字塔也是基于高斯金字塔得到的,对应N层高斯金字塔就有N-1层拉普拉斯金字塔,其数学公式为:
L i = G i − p y r U p ( p y r D o w n ( G i ) ) L_i=G_i-pyrUp(pyrDown(G_i)) Li=Gi−pyrUp(pyrDown(Gi))
即拉普拉斯金字塔第一层是将高斯金字塔的第一层减去高斯金字塔第二层上采样之后得到。

参考文献
Sift中尺度空间、高斯金字塔、差分金字塔(DOG金字塔)、图像金字塔
SIFT解析(一)建立高斯金字塔
数字图像处理(21): 图像金字塔(高斯金字塔 与 拉普拉斯金字塔)


