剑指offer113:课程顺序

题目：
现在总共有 numCourses 门课需要选，记为 0 到 numCourses-1。
给定一个数组 prerequisites ，它的每一个元素 prerequisites[i] 表示两门课程之间的先修顺序。 例如 prerequisites[i] = [ai, bi] 表示想要学习课程 ai ，需要先完成课程 bi 。
请根据给出的总课程数 numCourses 和表示先修顺序的 prerequisites 得出一个可行的修课序列。
可能会有多个正确的顺序，只要任意返回一种就可以了。如果不可能完成所有课程，返回一个空数组。
示例一：
输入: numCourses = 2, prerequisites = [[1,0]]
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例二：
输入: numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

示例三：
输入: numCourses = 1, prerequisites = []
输出: [0]
解释: 总共 1 门课，直接修第一门课就可。
分析：
将课程看成图中节点，如果两门课程存在先修顺序那么它们在图中对应的节点之间存在一条先修课程和后修课程的边，因此这是一个有向图。
numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]构建的有向图如下图

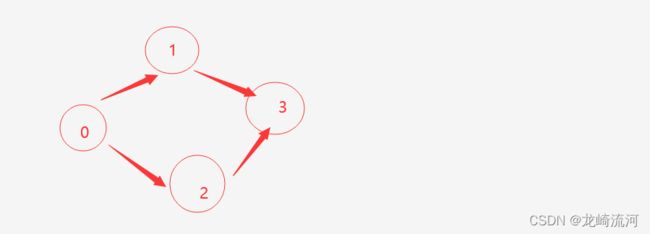
可行的修课序列实际上是图的拓扑排序序列，图中的每条边都是从先修课程指向后修课程，而拓扑排序能够保证任意一条边的起始节点一定排在终止节点的前面，因此拓扑排序得到的序列与先修顺序一定不会存在冲突，于是这个问题转变成如何求有向图的拓扑排序序列。
该题使用拓扑排序算法。
具体细节详细见代码。
代码：

package com.kuang;

import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class FindOrder {
    public int[] findOrder(int numCourses, int[][] prerequisites) {
//        先创建一个邻接表，键是先修课程，值是必须在键对应的课程之后学习的所有课程
        HashMap<Integer, List<Integer>> graph = new HashMap<>();
        for (int i = 0; i < numCourses; i++) {
            graph.put(i,new LinkedList<Integer>());
        }
//        将每个节点的入度保存到数组inDegrees中
        int[] inDegrees = new int[numCourses];
        for (int[] preq:prerequisites){
            graph.get(preq[1]).add(preq[0]);
//            preq[0]节点入度加1
            inDegrees[preq[0]]++;
        }
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (inDegrees[i] ==0){
                queue.add(i);
            }
        }
        List<Integer> order = new LinkedList<>();
        while (!queue.isEmpty()){
           int course = queue.remove();
           order.add(course);
           for (int next:graph.get(course)){
               inDegrees[next]--;
               if (inDegrees[next]==0){
                   queue.add(next);
               }
           }
        }
        return order.size() == numCourses ?order.stream().mapToInt(i->i).toArray():new int[0];
    }
}