高级数据结构

高级数据结构

二叉查找树

重复节点的插入应该如何处理?需要支持么?
1.重复的节点部分拉一条链出来,类似链表或者动态扩容数组
2.把这个新插入的数据当作大于这个节点的值来处理。

1、删除叶子节点

2、删除出度为1的节点

3、删除入读为2的节点

找到前驱或者后继替换后 转换为度为1的节点删除的问题

定义：

一个结点的后继，是大于x.key的最小关键字的结点。

一个结点的前驱，是小于x.key的最大关键字的结点。

完全二叉树、满二叉树，查找时间复杂度与树的高度成正比，O(h) —— O(logN)

与其他数据结构和算法相比,二叉查找树有什么优劣点?
都是查找,二叉查找树和hash相比有什么特点?

速度对比：

1. 哈希表的插入、删除、查找的时间复杂度都是 O(1)；
   而平衡二叉查找树的插入、删除、查找的时间复杂度都是 O(logn)。

2. 散列表扩容耗时很多，而且当遇到散列冲突时，性能不稳定，尽管二叉查找树的性能不稳定，但是在工程中，我们最常用的平衡二叉查找树的性能非常稳定，时间复杂度稳定在 O(logn)。

3. 笼统地来说，尽管散列表的查找等操作的时间复杂度是常量级的，但因为哈希冲突的存在，这个常量不一定比 logn 小，所以实际的查找速度可能不一定比 O(logn) 快。加上哈希函数的耗时，也不一定就比平衡二叉查找树的效率高。

操作对比/功能对比：

1. 散列表中的数据是无序存储的，如果要输出有序的数据，需要先进行排序。而对于二叉查找树来说，我们只需要中序遍历，就可以在 O(n) 的时间复杂度内，输出有序的数据序列。
2. 散列表的构造比二叉查找树要复杂，需要考虑的东西很多。比如散列函数的设计、冲突解决办法、扩缩容等。平衡二叉查找树只需要考虑平衡性这一个问题，而且这个问题的解决方案比较成熟、固定。

二叉查找树 代码演示

#include 
#include 
#include 

using namespace std;

typedef struct Node {
    int value, size;
    struct Node *left, *right;
} Node;

Node __NIL;  //哨兵节点
#define NIL (&__NIL)

__attribute__((constructor))
void init_NTL() {
    NIL->value = 0;
    NIL->size = 0;
    NIL->left = NIL->right = NIL;
}

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->value = key;
    p->size = 1;
    p->left = p->right = NIL;
    return p;
}

void update_size(Node *root) {
    root->size = root->left->size + root->right + 1;
    return ;
}

Node *insert(Node *root, int target) {
    if (root == NIL) return getNewNode(target);
    if (root->value == target) return root;
    if (root->value > targeet) {
        root->left = insert(root->left, target);
    } else {
        root->right = insert(root->right, target);
    }
    
    update_size(root);
    
    //root->size = 0;
    //if (root->left != NULL) root->size += root->left->size;
    //if (root->right != NULL) root->size += root->right->size;
    
    return root;
}

void clear(Node *root) {
    if (root == NIL) return ;
    clear(root->left);
    clear(root->right);
    free(root);
    return ;
}

int search(Node *root, int target) {
    if (root == NIL) return 0;
    if (root->value == target) return 1;
    if (root->value > target) {
        return search(root->left, target);
    }
    return search(root->right, target);
}

Node *predecessor(Node *root) {
    Node *p = root->left;
    while (p != NIL && p->right != NIL) {
        p = p->right;
    }
    return p;
}

Node *erase(Node *root, int target) {
    if (root == NIL) return root;
    if (root->value > target) {
        root->left = erase(root->left, target);
    } else if (root->value < target) {
        root->right = erase(root->right, target);
    } else {   
        //if (root->right == NULL && root->left == NULL) {  // 冗余操作
        //    free(root);
        //   return NULL;
        //} else 
        if(root->right == NIL || root->left == NIL) {
            Node *tmp = root->left != NIL ? root->left : root->right;
            free(root);
            return tmp;    //  返回不为空的节点
        } else {                 // 与前驱节点交换
            Node *tmp = predecessor(root); // 找到前驱节点
            root->value = tmp->value;    //删除当前根节点
            root->left = erase(root->left, tmp->value);   //删除原来根节点的前驱节点
        }
    }    
    update_size(root);
    return root;
}

void in_order(Node *root) {
    if (root == NIL) return ;
    in_order(root->left);
    printf("%d ", root->value);
    in_order(root->right);
    return ;
}

int find_k(Node *root, int k) { //求第k大的数
    if (root->right->size >= k) { // 右边 第k大的数
        return find_k(root->right, k);
    }
    if (root->right->size + 1 == k) {
        return root->value;
    }
    return find_k(root->left, k - root->right->size - 1); // 左边第（k - 右边节点）大的数
}

int main() {
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        int num = rand() % 100;
        printf("%d ", num);
        root = insert(root, num);
    }
 
    printf("\n");
    in_order(root);
    
    while (scanf("%d", &n) != EOF) {
        printf("delete node is %d\n", n);
        root = erase(root, n);
        in_order(root); printf("\n");
        printf("delete is success\n");
    }
    
    return 0;
}

Leetcode 110 Leetcode 669 剑指offer 54 Leetcode 450

平衡二叉树

AVL树

性质:
l H(left) - H(right) l <=1 左右子树高度差一
优点:
由于对每个节点的左右子树的树高做了限制，所以整棵树不会退化成一个链表

1、高度为H的BS 树，所包含的节点数量在什么范围之内?
H<= SIZE(H) <= 2^H - 1
2、高度为H的AVL树，所包含的节点数量在什么范围之内?
low(H - 2) + low(H - 1) + 1 <= SIZE(H) <= 2^H - 1 左右子树的最小高度的数量 + 根节点 = 当前高度最小数量

low(1) - 1, low(2) = 2, low(3) = 4, low(4) = 7; …

AVL 树

1. AVL 树 - 失衡条件
   LL 左子树的左子树多了 LR左子树的右子树多了(先小左旋(LL型)-在大右旋转)
   RR右子树的右子树多了 RL右子树的左子树多了(先小右旋(RR型)-在大左旋转)
2. 回溯的方式判断查看是否平衡

LL型

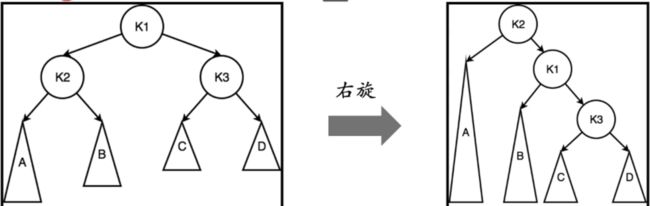
H1 = H2 + 1 K2 = K3 + 2(失衡) K2 = h1 + 1 K3 = max（h3， h4） + 1
H1 = h2 + 1 =max(h3, h4) + 2

LR型 先小左旋(LL型)-在大右旋转

K2 = K3 + 1 K3 = max(h2, h3) + 1 K3 = h1 + 1 K2 = h4 + 2(失衡)
K2 = h1 + 2 = max(h2, h3) + 2 = h4 + 2
h1 = max(h2, h3) =h4

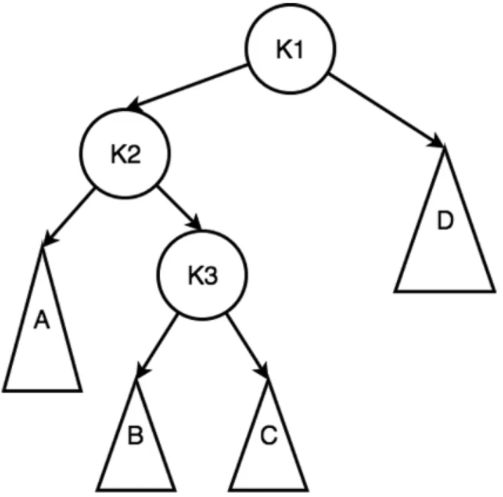
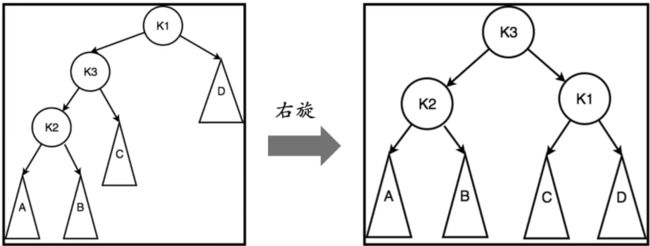
什么时候用AVL树

插入和删除操作较少，查找操作较多用AVL树，否则用BST树

AVL树是一种高度平衡的二叉树，所以查找的效率非常高，但是，有利就有弊，
AVL树为了维持这种高度的平衡，就要付出更多的代价。每次插入、删除都要做调整，
就比较复杂、耗时。所以，对于有频繁的插入、删除操作的数据集合，使用AVL树的代价就有点高了。

代码展示

左旋

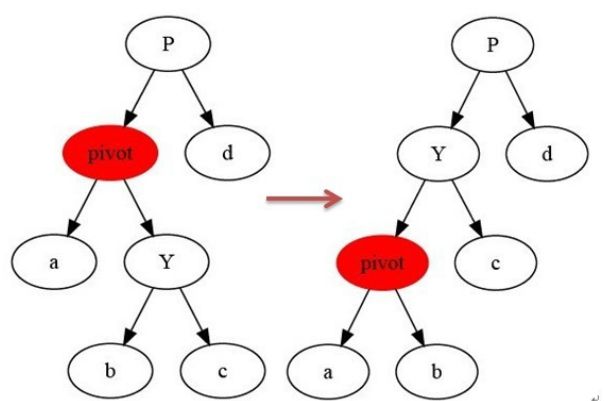
右旋

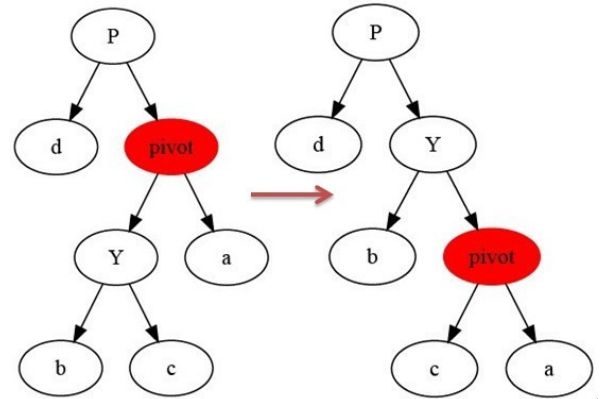
#include 
#include 
#include 
#include 
#include 

#define max(a, b) ((a) > (b) ? (a) : (b)) 

typedef struct Node {
    int value, h;
    struct Node* left, * right;
} Node;

Node __NIL;
#define NIL (&__NIL)
//_attribute__((constructor)) //如果函数被设定为constructor属性，则该函数会在main（）函数执行之前被自动的执行；
void init_NIL() {
    NIL->value = -1;
    NIL->h = 0;
    NIL->left = NIL->right = NIL;
    return;
}

Node* getNewNode(int target) {
    Node* p = (Node*)malloc(sizeof(Node));
    p->value = target;
    p->left = p->right = NIL;
    p->h = 1;
    return p;
}

void clear(Node* root) {
    if (root == NIL) return;
    clear(root->right);
    clear(root->left);
    free(root);
    return;
}

int search(Node* root, int target) {
    if (root == NIL) return 0;
    if (root->value == target) return 1;
    if (root->value > target) {
        return search(root->left, target);
    }
    return search(root->left, target);
}

void update_h(Node* root) {
    root->h = max(root->left->h, root->right->h) + 1;
    return;
}

Node* left_rotate(Node* root) {
    printf("left rotate : %d\n", root->value);
    Node* tmp = root->right;
    root->right = tmp->left;
    tmp->left = root;
    update_h(root);
    update_h(tmp);
    return tmp;
}

Node* right_rotate(Node* root) {
    printf("right rotate : %d\n", root->value);
    Node* tmp = root->left;
    root->left = tmp->right;
    tmp->right = root;
    update_h(root);
    update_h(tmp);
    return tmp;
}

const char* maintain_str[] = { "","LL", "LR", "RL", "RR" };

Node* maintain(Node* root) {
    if (abs(root->left->h - root->right->h) <= 1) return root;
    int maintain_type = 0;
    if (root->left->h > root->right->h) { // 证明左子树更高，失衡条件是L
        if (root->left->right->h > root->left->left->h) { // LR型
            root->left = left_rotate(root->left); //左旋
            maintain_type = 2; //LR
        }
        else {
            maintain_type = 1; //LL
        }
        root = right_rotate(root); //右旋
    }
    else { // 右子树比左子树更好，失衡条件是R
        if (root->right->left->h > root->right->right->h) { //RL型
            root->left = right_rotate(root->right); //右旋
            maintain_type = 3; //RL
        }
        else {
            maintain_type = 4; //RR
        }
        root = left_rotate(root); //左旋
    }
    printf("AVL maintain_type = %s\n", maintain_str[maintain_type]);
    return root;
}

Node* insert(Node* root, int target) {
    if (root == NIL) return getNewNode(target);
    if (root->value == target) return root;
    if (root->value > target) {
        root->left = insert(root->left, target);
    }
    else {
        root->right = insert(root->right, target);
    }
    update_h(root);
    return maintain(root);
}

Node* get_pre(Node* root) { // 前驱节点 前驱节点：当前节点左子树的最右节点，若无左子树，则：当前节点是其父节点的右子树
    Node* tmp = root;
    while (tmp->right != NIL) {
        tmp = tmp->right;
    }
    return tmp;
}

Node* erase(Node* root, int target) {
    if (root == NIL) return root;
    if (root->value > target) {
        root->left = erase(root->left, target);
    }
    else if (root->value < target) {
        root->right = erase(root->right, target);
    }
    else {
        if (root->left == NIL || root->right == NIL) {
            Node* tmp = (root->left != NIL) ? root->left : root->right;
            free(root);
            return tmp;
        }
        else {
            Node* tmp = get_pre(root->left);
            root->value = tmp->value;
            root->left = erase(root->left, tmp->value);
        }
    }
    update_h(root);
    return maintain(root);
}

void output(Node* root) {
    if (root == NIL) return;

    printf("(%d(%d) | %d , %d)\n", root->value, root->h, root->left->value, root->right->value);
    output(root->left);
    output(root->right);
}

int main() {
    init_NIL();
    srand(time(0));
    Node* root = NIL;
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        int val = rand() % 100;
        printf("\ninsert %d to tree: \n", val);
        root = insert(root, val);
        output(root);
    }
    clear(root);
    return 0;
}

字典树

Trie 字典树 单词树 前缀树

作用：单词查找 字符串排序 字符串匹配功能

利用树形结构，对空间优化，把很多前缀一样的进行存储

代码展示（1）

#include 
#include 
#include 
#include 

#define base 26


typedef struct Node {
    int flag;
    struct Node *next[base]; // [0] -> a, [1] -> b
} Node;

Node *getNewNode() {
    Node *p = (Node *)malloc(sizeof(Node));
    p->flag = 0;
    memset(p->next, 0, sizeof(Node *) * base);
    return p;
}

void clear(Node *root) {
    if(root == NULL) return ;
    for(int i = 0; i < base; i++) {
        clear(root->next[i]);
    }
    free(root);
    return ;
}

void insert(Node *root, const char *str) {
    Node *p = root;
    for(int i = 0; str[i]; i++) {
        int ind = str[i] - 'a';
        if(p->next[ind] == NULL) p->next[ind] = getNewNode();
        p = p->next[ind]; }
    p->flag = 1;
    return ;
}

int find(Node *root, const char *str) {
    Node *p = root;
    for(int i = 0; str[i]; i++) {
        int ind = str[i] - 'a';
        p = p->next[ind];
        if(p == NULL) return 0;
    }
    return p->flag;
}

void output(Node *root, int k, char *buff) {
    if(root == NULL) return ;
    buff[k] = '\0';
    if(root->flag) {
        printf("%s\n", buff);
    }
    for(int i = 0; i < base; i++) {
        buff[k] = 'a' + i;
        output(root->next[i], k + 1, buff);
    }
    return ;
}

int main() {

    int op;
    char str[100];
    Node *root = getNewNode();
    while(scanf("%d", &op) != EOF) {
        switch (op) {
            case 1: {
                scanf("%s", str);
                printf("insert %s to tire\n", str);
                insert(root, str);
            } break;
            case 2: {
                scanf("%s", str);
                printf("find %s in tree = %d\n",str, find(root, str));
            } break;
            case 3: {
                char buff[100];
                output(root, 0, buff);
            } break;
        }
    }
    clear(root);
    return 0;
}

Trie树的优缺点

优点︰查找高效,并且利用前缀来节约空间
缺点∶空间复杂度过高

1、空间上的不确定性
2、输入上的不确定性

无法利用CPU缓存，无法名字

思考∶如何解决空间复杂度过高的问题? 缩点

1、hash
2、平衡查找树

1. 完全二叉树，实际存储结构是连续数组空间，思维逻辑结构是树型的
2. 完全二叉树，节省了大量的存储边的空间
3. 优化思想：记录式 改 计算式
4. $n$ 个节点的字典树，有效使用 $n-1$ 条边，浪费了 $(k-1)\ast n+1$ 条边的存储空间
5. 参考完全二叉树的优点，提出了双数组字典树

oj.281

代码展示（2） 利用数组存储字典树

竞赛字典树实现方式

#include 
#include 
#include 
#include 

const int maxn = 1e6 + 10;
const int base = 26;

struct Node {
    int cnt;
    int next[base]; // address -> index         数组：数的计算代替地址的存储
} tree[maxn];  // 字典树  最多有maxn个

// 0 --  root 第一层        

int root = 0, node_cnt = 1;  
char str[maxn];

int getNewNode() {
    return node_cnt++;
}

void insert(const char *str) {
    int p = root;
    for(int i = 0; str[i]; i++) {
        int ind = str[i] - 'a';
        if(tree[p].next[ind] == 0) {
            tree[p].next[ind] = getNewNode(); //对于没有下一层的字母-申请新的一层
        } 
        p = tree[p].next[ind];
    }
    tree[p].cnt += 1;
    return ;
}

int find(const char *str) {
    int p = root;
    int ans = 0;
    for(int i = 0; str[i]; i++) {
        int ind = str[i] - 'a';
        p = tree[p].next[ind];
        if(p == 0) return ans;
        ans += tree[p].cnt;
    }
    return ans;
}

int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i++) {
        scanf("%s", str);
        insert(str);
    }
    for(int i = 0; i < m; i++) {
        scanf("%s", str);
        printf("%d\n", find(str));
    }

    return 0;
}

oj.282

#include 
#include 
#include 
#include 

const int maxn = 3200000 + 10;  //32 * 1e5     1e5个数字，每个数字最多申请32个不同的层
const int max_k = 30;  //31位为符号位  0~30位为值
struct node {
    int flag;
    int next[2];
} tree[maxn];
int root = 0, node_cnt = 1;

int getnewnode() {
    return node_cnt++;
}

void insert(int x) {
    int p = root;
    for(int i = max_k; i >= 0; i--) { //二进制的形式遍历 从大到小存储
        int ind = !!(x & (1 << i));// 拿到x的第i位
        /*
        两个感叹号由此推导可以知道：
		！！（非零）=1
		！！（零）=0
		*/
        if(tree[p].next[ind] == 0) {
            tree[p].next[ind] = getnewnode();
        }
        p = tree[p].next[ind];
    }
    tree[p].flag = 1;
    return ;
}

int find(int x) {
    int p = root;
    int ans = 0;
    for(int i = max_k; i >= 0; i--) { //二进制的形式遍历 从大到小查找
        int ind = !(x & (1 << i));
        if(tree[p].next[ind]) {
            ans |= (1 << i);    //异或 相加
            p = tree[p].next[ind];
        } else {
            p = tree[p].next[!ind];
        }
    }
    return ans;
}

int main() {
    int n, ans = 0;
    scanf("%d", &n);
    for(int i = 0, val, fval = 0; i < n; i++) {
        scanf("%d", &val);
        if(i) fval = find(val);
        ans = fval > ans ? fval : ans;
        insert(val);
    }
    printf("%d\n", ans);

    return 0;
}

int ind = !!(x & (1 << i));// 拿到x的第i位
两个感叹号由此推导可以知道：
！！（非零）=1
！！（零）=0
！！—— 归一化

双数组字典树

1. 顾名思义，两个数组代表一棵字典树结构
2. base 数组信息与子节点编号相关，base + i 就是第 i 个子节点编号
3. check 数组信息负责做【亲子鉴定】，check 数组中用正负表示是否独立成词
4. 不擅长进行动态插入操作
5. 一次建立，终身使用
6. 为了方便，基于普通字典树实现的双数组字典树

DATrie 离线构建，在线查询

base[s] + c = t
check[t] =  s

check 负号 表示独立成词

1为根节点

最长回文子串

马拉车算法 —— 充分利用对称性

d[k] 以k为中心最长的回文长度

d[i] = min(r - i, d[j] ) 如果d[j]长度超过r-i，并且此时d[i] = d[j]则说明 超过r的部分关于k也是对称的，r是错误的，r应该更长，所以不成立。

所以当d[j] < r- i 时，d[i] < d[j]，否则 d[i] = r-i ; 少暴力一段

class Solution {
public:
    string getNewString(string s) {
        string ns = "#";
        for(int i = 0; s[i]; i++) {  //abcd  #a#b#c#d#  减少判断方式  奇数：中心对称    偶数：两边对称
            (ns += s[i]) += "#";
        }
        return ns;
    }

    string longestPalindrome(string s) {
        if(s.size() == 0) return "";
        string ns = getNewString(s);
        vector dis(ns.size());
        int l = 0, r = -1;
        for(int i = 0; i < ns.size(); i++) {
            if(i > r) { dis[i] = 1;} 
            else { dis[i] = min(dis[l + r - i], r - i);}
            while(i - dis[i] >= 0 && i + dis[i] < ns.size()
                && ns[i - dis[i]] == ns[i + dis[i]]) { //暴力匹配
                    dis[i]++; //半径
                }
            if(i + dis[i] > r && i - dis[i] > 0) {
                l = i - dis[i];
                r = i + dis[i];
            }
        }
        string ret;
        int tmp = 0;
        for(int i = 0; ns[i]; i++) {
            if(tmp >= dis[i]) continue;
            tmp = dis[i];
            ret = "";
            for(int j = i - dis[i] + 1; j < i + dis[i]; j++) {
                if(ns[j] == '#') continue;
                ret += ns[j];
            }
        }
        return ret;
    }
};

并查集

#include 
#include 

#define maxn 1000010

int p[maxn];

int find(int x) {
    if (p[x] != x) {
        return p[x] = find(p[x]); 
    }
    return p[x];
}

void merge(int x, int y) {
	int fx = find(x);
    int fy = find(y);
    if (fx != fy) {
        p[fx] = fy;
    }
    return ;
}

int main() {
    int n, m, a, b;
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i++) {
        p[i] = i;
    }
    for (int i = 0; i < m; i++) {
        scanf("%d%d", &a, &b);
    }
    int ans = 0;
    for (int i = 0; i < n; i++) {
        ans += (p[i] == i);
    }
    
	return 0;   
}

冗余连接 II

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

满足下列条件的有向图被称为有向树:
(1) 有且仅有一个结点的入度为0;
(2) 除树根外的结点入度为1;
(3) 从树根到任一结点有一条有向通路。

无环 ，入度<=1

class Solution {
public:
    /*
        思路 : 逐个删除边, 判断剩下的图, 是不是一个有向树
        判断思路 : 
            1. 有且只有一个节点入度为0 
            2. 删除边后，除树根外的结点入度为1      (无环  且<2)
    */


    int p[5000], flag1 = 0, flag2 = 0;
    
    int find(int x) {
        if(p[x] != x) return p[x] = find(p[x]);
        return p[x];
    }
    void union_find(int x, int y) {
        int fx = find(x);
        int fy = find(y);
        if(fx != fy) {
            p[fx] = fy;
        } else {
            flag1 = 1; // 要进行连接的两个集合，之前不能已经连接了，否则就成环了
        }
    }

    vector findRedundantDirectedConnection(vector>& edges) {
        int vis[5000] = {0};
        for(int i = edges.size() - 1; i >= 0; i--) { // 逐个删除边
            flag1 = 0, flag2 = 0;
            int x = edges[i][0];
            int y = edges[i][1];
            memset(vis, 0, sizeof(vis));
            for(int k = 0; k < 5000; k++) {
                p[k] = k;
                vis[k] = 0; // 入度为数组, 初始化为0
            }
            for(int j = 0; j < edges.size(); j++) {
                if(edges[j][0] == x && edges[j][1] == y) { // 删除的那条边
                    continue;
                }
                union_find(edges[j][0], edges[j][1]); // 并查集  加入
                if(flag1 == 1) break;

                // 入度+1
                vis[edges[j][1]]++;
                if(vis[edges[j][1]] > 1) {
                    flag2 = 1;
                    break;
                }
            }
            if(flag1 == 0 && flag2 == 0) {
                return {x, y};
            }
        }
        return edges[0]; // 随便一个返回值, 要不编译不过
    }
};

最小生成树

kurskal(基于并查集)

1、sort 边 从小到大
2、遍历边 （并查集，判断有无环）
3、边两边的点加入T

给邻接图求最小生成树的长度

#include 
#include 
#include 

using namespace std;

const int maxn = 1e4 + 10;

int p[maxn];
struct edge {
    int v, u, c;
};

bool cmp(edge x, edge y) {
    return x.c < y.c;
}

vector e;

int find(int x) {
    if(p[x] != x) return p[x] = find(p[x]);
    return p[x];
}

int union_find(int x, int y) {
    int fx = find(x);
    int fy = find(y);
    if(fx != fy) {
        p[fx] = fy;
        return 1; // 无环
    }
    return 0;  //有环
}

int main() {
    int n, x;
    scanf("%d", &n);
    for(int i = 0; i <= n; i++) {
        p[i] = i;
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            scanf("%d", &x);
            if(i == j) continue;
            e.push_back({i, j, x});
        }
    }
    sort(e.begin(), e.end(), cmp);
    int ans = 0;
    for(int i = 0; i < e.size(); i++) {
        int v = e[i].v, u = e[i].u, c = e[i].c;
        if(union_find(v, u)) {
            ans += c;    
        }    
    }
    
    printf("%d\n", ans);
    
    return 0;
}

prim解法 选离集合最近的点 更适合邻接矩阵

#include 
#include 
#include 
#include 
#include 
#include 
#include 

字符串匹配算法

朴素匹配算法Brute-Force

时间复杂度O(N*M)

#include 
#include 

int brute_force(const char *s, const char *t) {
    for (int i = 0; s[i]; i++) {
        int flag = 0;
        for (int j = 0; t[j]; j++) {
            if (s[i + j] == t[j]) continue;
            flag = 1;
            break;
        }
        if (flag == 0) return i;
    }
    return -1;
}

int main() {
    
    char s[100], t[100];
    scanf("%s%s", s, t);
    printf("%d\n", brute_force(s, t));
    
    return 0;
}

hash Rabin-Karp匹配法

对母串的每一个字串进行hash n-m+1次hash hash(A) = hash(B) A=B

hash 的方法 abc = a * 26 * 26 + b * 26 + c

前一个：aeca hash(A) 后一个：ecae hash(B) hash(B) = hash(A) - (a * 26 * 26 * 26) + e

推导公式 h[i] = (h[i - 1] - 26 ^ (m - 1) * s[i - 1]) * 26 + s[i + m - 1]

问题：
1、hash值超过了int范围？

优化hash函数, 把字符与素数做映射, 而不是简单的a->1, b->2

优化hash函数, 更改hash策略, 直接把对应位置想加, 不做乘法法

2、hash冲突？ 发送冲突，则直接对比 （子字符串）

时间复杂度：
最好：O(N)
最坏：O(N*M) (发送哈希冲突次数过多)

KMP算法

母串S

模式串T

一、关键点：求模式串 的每一个前缀的子前缀的相等的最长前缀和后缀

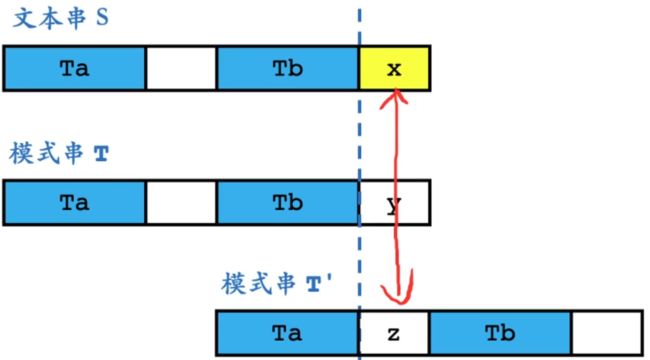
x!=y: 对比x和z

abcdab

子前缀	其相等的最长前缀和后缀
a	a
ab	无
abc	无
abcd	无
abcda	a
abcdab	ab

二、最长前缀后缀预处理

i = j 扩大 Sa 和 Sb，

i != j 利用sa和sb的最长前缀和后缀，再对比 i 和 j

如：模式串T abcxabcab

#include 
#include 

int next[100];

int kmp(const char *s, const char *t) { //s为母串， t为子串
	
    //init next
	next[0] = -1; //第一个字符的前后缀无意义
    
    for(int i = 0, j = -1; t[i]; i++) { //最长前缀后缀预处理
        while(j != -1 && t[j + 1] != t[i]) { //j!= -1 跳过第一个  t[j + 1] != t[i]第二种情况
            j = next[j]; //利用sa和sb的最长前缀和后缀，再对比	i 和 j + 1
        }
        if (t[j + 1] == t[i]) { // t[j + 1] == t[i]   扩大 Sa 和 Sb
            j++;
        }
        next[i] = j;  //存 当前最长值
    }    
    
    /*
	for (int i = 0; i < 20; i++) { //next[i] 默认-1，加一即为真实值
        printf("%d ", next[i]);
    }
    printf("\n");
    */
    
    //match string
    for(int i = 0, j = -1; s[i]; i++) {
        while(j != -1 && s[i] != t[j + 1]) {
            j = next[j];
        }
        if (s[i] == t[j + 1]) j++;
        if (t[j + 1] == '\0') return i - j; //返回位置
    }
    return -1;

}

int main() {
    char s[100], t[100];
    scanf("%s%s", s, t);
    kmp(s, t)；
    printf("%d\n", kmp(s, t));
    
    return 0;
}

无注释版

int next[100];

int kmp(const char *s, const char *t) {
    // init next
    next[0] = -1;
    for(int i = 1, j = -1; t[i]; i++) {
        while(j != -1 && t[j + 1] != t[i]) { j = next[j]; }
        if(t[j + 1] == t[i]) { j++; }
        next[i] = j;
    }
    // match string
    for(int i = 0, j = -1; s[i]; i++) {
        while(j != -1 && s[i] != t[j + 1]) { j = next[j]; }
        if(s[i] == t[j + 1]) j++;
        if(t[j + 1] == '\0') return i - j;
    } 
    return -1;
}

kmp 流式算法
a.out < input 512MB的内存处理10GB

hash算法
BM算法
Sunday算法

Sunday算法

1. SUNDAY 算法理解的核心，在于理解对齐点位
2. 是文本串的匹配尾部，一定会出现在模式串中的字符
3. 文本串应该和模式串中最后一位(从后往前找的第一位)出现该字符的位置对齐
4. 第一步：预处理**每一个字符（所有）**在模式串中最后一次出现的位置
5. 第二步：模拟暴力匹配算法过程，失配的时候，文本串指针根据预处理信息向后移动若干位

int sunday(const char *s, const char *t) {
    int len_s = strlen(s), len_t = strlen(t);
    int ind[256];
    
    //第一步：预处理每一个字符（所有 256个字符）在模式串中最后一次出现的位置
    for (int i = 0; i < 256; i++) ind[i] = len_t + 1;
    for (int i = 0; t[i]; i++) {
        ind[t[i]] = len _t - i;
    }
    
    int i = 0;
    while (i + len_t <= len_s) {
        int flag = 1;
        for (int j = 0; t[j]; j++) {
            if (s[i + j] == t[j]) continue;
            flag = 0;
            break;
        }
        if (flag == 1) return i; // 找到了匹配, 直接返回位置
        i += ind[s[i + len_t]]; // 匹配不成功, 找对齐点位, 出现在第几位, 就往后移动多少位置
    }
    return -1;
}

SHIFT-AND算法

模式串T转换为二维数组

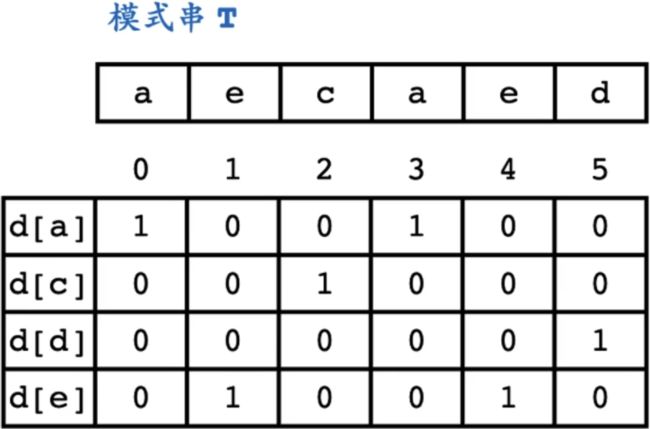
d[a] = int(001001) 反过来

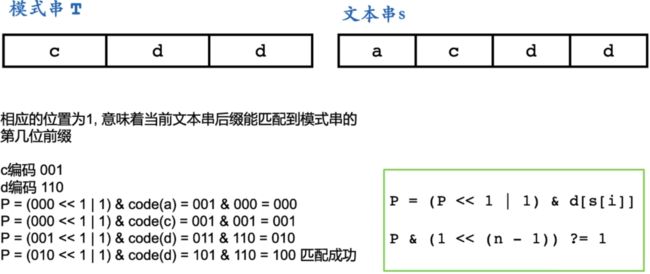
P = （P << 1 | 1) & d[s[i]]

P & (1 << (n - 1))

SHIFT-AND算法

1. 第一步对模式串做特殊处理，把每一种字符出现的位置，转换成相应的二进制编码

2. 后续匹配的过程中跟模式串一毛钱关系都没有

3. P的结构定义:
   相应的位置为1,意味着当前文本串后缀能匹配到模式串的第几位前缀

4. P的结构操作:
   文本串进来一个,对于每个p为1的地方,都有可能移动1位(都有可能多匹配一个字符),并且第一位O也有可能变成1,我们先假设,所有的1都能匹配得到假设完之后,开始验证我们的假设

时间复杂度 O(n+m)

#include 
#include 

int shift_and(const char *s, const char *t) {
    int code[256] = {0};
    int n = 0;
    for(int i = 0; t[i]; i++, n++) {
        code[t[i]] |= (1 << i); //t[i]  位置 加上 第i位的1
    }
    int p = 0;
    for(int i = 0; s[i]; i++) {
        p = (p << 1 | 1) & code[s[i]];
        if(p & (1 << (n - 1))) return i - n + 1; // 和t的n个前缀相等则完成字符串匹配
    }
    return -1;
}

int main() {
    
    char s[100], t[100];
    scanf("%s%s", s, t);
    printf("%d\n", shift_and(s, t));
    
    return 0;
}

练习题:
给出一个正则表达式，形如:
(alb|c) &(c /d)&e& (f|a|b)
再给出一段文本，问文本中有多少段不同的子文本可以被上述
正则表达式匹配。

AC 自动机

kmp的基础上做的多模式匹配

多模匹配问题

1. 有多个模式串的匹配问题，就是多模匹配问题
2. Step1：多个模式串，建立成一棵字典树
3. Step2：和文本串的每一位对齐匹配，模拟暴力匹配算法的过程

AC 自动机的思想

1. 当匹配成功文本串中的 she 时，也就意味着后续一定会匹配成功 he
2. she 对应了字典树中的节点 P，he 对应了字典树中的节点Q
3. P 和 Q 就是等价匹配节点，如果从 P 引出一条边指向 Q，就可以加速匹配过程
4. 在 P 下面查找节点的操作，等价于在 Q 下面查找节点的操作
5. 这条等价关系边，通常在 AC 自动机上叫做 【Fail 指针】
6. AC 自动机 = Trie + Fail 指针
7. 子节点的 Fail 指针是需要参照父节点的 Fail指针信息的，最简单的建立方式，就是采用【层序遍历】
8. 没做优化的 AC 自动机，本质上是一个 NFA（非确定型有穷状态自动机）
9. 通俗理解：根据当前状态 p，以及输入字符 c，无法通过一步操作确定状态
10. 第二种理解：当前状态，并不代表唯一状态。

#include 
#include 
#include 
#include 

#define base 26

typedef struct Node {
    const char *str;
    struct Node *next[base], *fail;
} Node;

typedef struct Queue {
    Node **data;
    int head, tail;
} Queue;

Queue *initQueue(int n) {
    Queue *q = (Queue *)malloc(sizeof(Queue));
    q->data = (Node **)malloc(sizeof(Node *) * n);
    q->head = q->tail = 0;
    return q;
}

int empty(Queue *q) {
    return q->tail - q->head == 0;
}

Node *front(Queue *q) {
    return q->data[q->head];
}

void push(Queue *q, Node *node) {
    q->data[q->tail++] = node;
}

void pop(Queue *q) {
    if(empty(q)) return ;
    q->head++;
    return ;
}

void clearQueue(Queue *q) {
    if(q == NULL) return ;
    free(q->data);
    free(q);
    return ;
}

int node_cnt = 0;
Node *getNewNode() {
    Node *p = (Node*)malloc(sizeof(Node));
    p->str = NULL;
    p->fail = NULL;
    node_cnt++;
    memset(p->next, 0, sizeof(Node *) * base);
    return p;
}

void clear(Node *root) {
    if(root == NULL) return ;
    for(int i = 0; i < base; i++) {
        clear(root->next[i]);
    }
    if(root->str) free((char *)root->str);
    free(root);
    return ;
}

const char *copyStr(const char *s) {
    int n = strlen(s);
    char *buff = (char *)malloc(n + 1);
    strcpy(buff, s);
    return buff;
}

void insert(Node *root, const char *s) {
    Node *p = root;
    for(int i = 0; s[i]; i++) {
        if(p->next[s[i] - 'a'] == NULL) {
            p->next[s[i] - 'a'] = getNewNode();
        }
        p = p->next[s[i] - 'a'];
    }
    p->str = copyStr(s);
    
    return ;
}

void initBuildFaildQueue(Node *root, Queue *q) { //队列 root->next[i]先进先出
    root->fail = NULL;
    for(int i = 0; i < base; i++) {
        if(root->next[i] == NULL) continue;
        root->next[i]->fail = root;
        push(q, root->next[i]);
    }
    return ;
}

void build_fail(Node *root) {
    Queue *q = initQueue(node_cnt);
    initBuildFaildQueue(root, q);
    while(!empty(q)) {
        Node *p = front(q);
        for(int i = 0; i < base; i++) {
            if(p->next[i] == NULL) continue;
            Node *k = p->fail;
            while(k != root && k->next[i] == NULL) {
                k = k->fail;
            }
            if(k->next[i] != NULL) k = k->next[i];
            p->next[i]->fail = k;
            push(q, p->next[i]);
        }
        pop(q);
    }
    clearQueue(q);
    return ;
}

void match_ac(Node *root, const char *s) {
    Node *p = root, *q;
    for(int i = 0; s[i]; i++) {
        while(p != root && p->next[s[i] - 'a'] == NULL) {
            p = p->fail;
        }
        if(p->next[s[i] - 'a']) p = p->next[s[i] - 'a'];
        q = p;
        while(q) {
            if(q->str != NULL) printf("find %s\n", q->str);
            q = q->fail;
        }
    }
    return ;
}


int main() {
    int n;
    char s[100];
    Node *root = getNewNode();

    scanf("%d", &n);
    for(int i = 0; i < n; i++) {
        scanf("%s", s);
        insert(root, s);
    }
    build_fail(root);
    scanf("%s", s);
    match_ac(root, s);
    return 0;
}

经验O(N)

AC自动机的优化（有点类似并查集的路径压缩）

#include 
#include 
#include 
#include 

#define base 26

typedef struct Node {
    const char *str;
    struct Node *next[base], *fail;
} Node;

typedef struct Queue {
    Node **data;
    int head, tail;
} Queue;

Queue *initQueue(int n) {
    Queue *q = (Queue *)malloc(sizeof(Queue));
    q->data = (Node **)malloc(sizeof(Node *) * n);
    q->head = q->tail = 0;
    return q;
}

int empty(Queue *q) {
    return q->tail - q->head == 0;
}

Node *front(Queue *q) {
    return q->data[q->head];
}

void push(Queue *q, Node *node) {
    q->data[q->tail++] = node;
}

void pop(Queue *q) {
    if(empty(q)) return ;
    q->head++;
    return ;
}

void clearQueue(Queue *q) {
    if(q == NULL) return ;
    free(q->data);
    free(q);
    return ;
}

int node_cnt = 0;
Node *getNewNode() {
    Node *p = (Node*)malloc(sizeof(Node));
    p->str = NULL;
    p->fail = NULL;
    node_cnt++;
    memset(p->next, 0, sizeof(Node *) * base);
    return p;
}

void clear(Node *root) {
    if(root == NULL) return ;
    for(int i = 0; i < base; i++) {
        clear(root->next[i]);
    }
    if(root->str) free((char *)root->str);
    free(root);
    return ;
}

const char *copyStr(const char *s) {
    int n = strlen(s);
    char *buff = (char *)malloc(n + 1);
    strcpy(buff, s);
    return buff;
}

void insert(Node *root, const char *s) {
    Node *p = root;
    for(int i = 0; s[i]; i++) {
        if(p->next[s[i] - 'a'] == NULL) {
            p->next[s[i] - 'a'] = getNewNode();
        }
        p = p->next[s[i] - 'a'];
    }
    p->str = copyStr(s);
    
    return ;
}

void initBuildFaildQueue(Node *root, Queue *q) {
    root->fail = NULL;
    for(int i = 0; i < base; i++) {
        if(root->next[i] == NULL) {
            root->next[i] = root;
            continue;
        }
        root->next[i]->fail = root;
        push(q, root->next[i]);
    }
    return ;
}

void build_fail(Node *root) {
    Queue *q = initQueue(node_cnt);
    initBuildFaildQueue(root, q);
    while(!empty(q)) {
        Node *p = front(q);
        for(int i = 0; i < base; i++) {
            if(p->next[i] == NULL) {
                p->next[i] = p->fail->next[i]; 
                continue;
            } 
            Node *k = p->fail->next[i];
            p->next[i]->fail = k;
            push(q, p->next[i]);
        }
        pop(q);
    }
    clearQueue(q);
    return ;
}

void match_ac(Node *root, const char *s) {
    Node *p = root, *q;
    for(int i = 0; s[i]; i++) {
        p = p->next[s[i] - 'a'];
        q = p;
        while(q) {
            if(q->str != NULL) printf("find %s\n", q->str);
            q = q->fail;
        }
    }
    return ;
}


int main() {
    int n;
    char s[100];
    Node *root = getNewNode();

    scanf("%d", &n);
    for(int i = 0; i < n; i++) {
        scanf("%s", s);
        insert(root, s);
    }
    build_fail(root);
    
    scanf("%s", s);
    match_ac(root, s);



    return 0;
}

字符串统计题

蒜头君某一天学习了 nn 个单词，他想看篇文章来复习下今天学习的内容，现在他想知道每个单词在这篇文章里分别出现了多少次，聪明的你能帮他解决这个问题吗？

输入格式

第一行输入一个整数 nn（1 \leq n \leq 10001≤n≤1000），表示蒜头君学习的 nn 个单词。

接下来 nn 行，每行输入一个字符串，仅由小写字母组成，长度不超过 2020。

最后输入一个字符串 SS，仅由小写字母组成，长度不超过 10^5105，表示蒜头君看的文章。

输出格式

依次输出 nn 行，每行输出格式为i: num，ii 表示单词的编号（从 00 开始编号），numnum 为一个整数，表示第 ii 个单词在母串 SS 中出现了 numnum 次。

样例输入复制

2
ab
bca
abcabc

样例输出复制

0: 2
1: 1

#include 
#include 

#define base 26
const int maxn = 1e5 + 10;


struct Node {
    int flag, *cnt;
    int next[base], fail;
} tree[maxn];

int *ans[maxn];
int que[maxn], head, tail;
int root = 1, cnt = 2;
char s[maxn + 10];
int n;

int getNewNode() {
    return cnt++;
}

int *insert(const char *s) {
    int p = root;
    for(int i = 0; s[i]; i++) {
        int ind = s[i] - 'a';
        if(tree[p].next[ind] == 0) tree[p].next[ind] = getNewNode();
        p = tree[p].next[ind];
    }
    tree[p].flag = 1;
    if(tree[p].cnt == NULL) {
        tree[p].cnt = (int *)malloc(sizeof(int));
        tree[p].cnt[0] = 0;
    }

    return tree[p].cnt;
}

void build_ac() {
    head = tail = 0;
    tree[root].fail = 0;
    for(int i = 0; i < base; i++) {
        if(tree[root].next[i] == 0) {
            tree[root].next[i] = root;
            continue;
        }
        tree[tree[root].next[i]].fail = root;
        que[tail++] = tree[root].next[i];        
    }
    
    while(head < tail) {
        int p = que[head++];
        for(int i = 0; i < base; i++) {
            int c = tree[p].next[i], k = tree[p].fail;
            if(c == 0) {
                tree[p].next[i] = tree[k].next[i];
                continue;
            }
            k = tree[k].next[i];
            tree[c].fail = k;
            que[tail++] = c;
        }
    }
    return ;
}


void match_ac(const char *s) {
    int p = root;
    for(int i = 0; s[i]; i++) {
        int ind = s[i] - 'a';
        p = tree[p].next[ind];
        int q = p;
        while(q) {
            if(tree[q].flag) {
                tree[q].cnt[0]++;
            }
            q = tree[q].fail;
        }
    }
    return ;
}


int main() {
    scanf("%d", &n);
    for(int i = 0; i < n; i++) {
        scanf("%s", s);
        ans[i] = insert(s);
    }
    build_ac();

    scanf("%s", s);
    match_ac(s);

    for(int i = 0; i < n; i++) {
        printf("%d: %d\n", i, *ans[i]);
    }
    
    return 0;
}

逆波兰式

#include 
#include 
#include 

const int inf = 0x3f3f3f3f;

char str[1000];

int calc(char *str, int l, int r) { // l起始位置， r末尾位置，借用系统栈
    int pos = -1, pri = inf - 1;
    int temp = 0;
    for(int i = l; i <= r; i++) {
        int cur = inf;
        switch(str[i]) {
            case '(': temp += 100; break;
            case ')': temp -= 100; break;
            case '+':
            case '-': cur = temp + 1; break;
            case '*':
            case '/': cur = temp + 2; break;
        }
        if(cur <= pri) { //选择优先级最小的
            pos = i, pri = cur;
        }
    }
    
    if(pos == -1) { //无符号了
        int num = 0;
        for(int i = l; i <= r; i++) {
            if(str[i] < '0' || str[i] > '9') continue;
            num = num * 10 + (str[i] - '0');
        }
        return num;
    }
    int a = calc(str, l, pos - 1);
    int b = calc(str, pos + 1, r);
    switch(str[pos]) {
        case '+' : return a + b;
        case '-' : return a - b;
        case '*' : return a * b;
        case '/' : return a / b;
    }
    
    return 0;
}

int main() {

    scanf("%s", str);
    printf("\n%d\n", calc(str, 0, strlen(str) - 1));

    return 0;
}

优先队列

优先队列是性质 堆是结构

植物大战僵尸

蒜头君最近迷恋上了一款游戏：植物大战僵尸。在梦中，他梦到了一个更加刺激的植物大战僵尸版本。有 nn 个僵尸从起点出发，编号从 11 到 nn，每个僵尸占用一个独立的直线道路。第 ii 个僵尸在第一秒的速度为 f_if**i ，之后的速度为 s_is**i 。蒜头君在每一秒结束时，都会选择一个跑在最前面的僵尸（如果存在多个僵尸处于最前面，则选择编号最小的僵尸），使用能量豆将其消灭。

求蒜头君消灭僵尸的顺序。

输入格式

第一行输入一个整数 TT（T \leq 20T≤20），表示有 TT 组测试数据，对于每组测试数据：

第一行包含一个整数 nn（1 \leq n \leq 50,0001≤n≤50,000）。

接下来 nn 行，每行包含两个整数 f_if**i 和 s_is**i（0 \leq f_i \leq 5000≤f**i≤500，0 < s_i \leq 1000<s**i≤100）。

输出格式

对于每组测试数据，第一行输出Case #c:，其中 cc 表示测试数据编号；第二行输出 nn 个整数，表示僵尸被消灭的顺序，每两个整数之间一个空格，最后一个整数后面没有空格。

样例输入复制

2
3
10 2
9 3
8 4
6
1 1
2 2
3 3
4 4
5 5
6 1

样例输出复制

Case #1:
1 2 3
Case #2:
6 5 4 3 2 1

#include 
#include 
#include 

const int maxn = 5e4 + 10;

#define swap(a, b) { \
    __typeof(a) c = a; \
    a = b, b = c; \
}

typedef struct data {
    int n, f,s;
} data;

data heap[200][maxn];

int gt(data a, data b) {
    if(a.f != b.f) {
        return a.f > b.f;
    }
    return a.n < b.n;
}

void push(data *h, data val) {
    h[++h[0].n] = val;
    int ind = h[0].n;
    while(ind / 2 && gt(h[ind], h[ind / 2])) {
        swap(h[ind], h[ind / 2]);
        ind /= 2;
    }
    return ;
}

void pop(data *h) {
    swap(h[1], h[h[0].n]);
    h[0].n--;
    int ind = 1, temp;
    while(ind * 2 <= h[0].n) {
        temp = ind;
        if(gt(h[ind * 2], h[temp])) temp = ind * 2; 
        if(ind * 2 + 1 <= h[0].n && gt(h[ind * 2 + 1], h[temp])) {
            temp = ind * 2 + 1;
        }
        if(temp == ind) break;
        swap(h[temp], h[ind]);
        ind = temp;
    }
    return ;
}

int empty(data *h) {
    return h[0].n == 0;
}

data top(data *h) {
    return h[1];
}

void clear(data *h) {
    h[0].n = 0;
}

void init_heap() {
    for(int i = 0; i <= 100; i++) {
        clear(heap[i]);
    }
    return ;
}

void solve() {
    init_heap();
    int n, f, s;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d%d", &f, &s);
        data tmp = {i, f, s};
        push(heap[s], tmp);
    }
    
    for(int i = 1; i <= n; i++) {
        int ind = 0, pos = 0; //跑的最快的僵尸, 在ind堆中, pos记录位置
        for(int j = 1; j <= 100; j++) {
            if(empty(heap[j])) continue;
            // 第i秒, 速度为j的僵尸, 应该在的位置 = 时间 * 速度 + 初始位置
            int cur_pos = (i - 1) * j + top(heap[j]).f;
            if(ind == 0) {
                ind = j, pos = cur_pos;
                continue;
            }
            if(pos < cur_pos || ((pos == cur_pos) && top(heap[j]).n < top(heap[ind]).n)) {
                ind = j, pos = cur_pos;
            }
        }
        if(i != 1) printf(" ");
        printf("%d", top(heap[ind]).n);
        pop(heap[ind]);
    }
    printf("\n");
    return ;
}


int main() {
    int T, i = 0;
    scanf("%d", &T);
    while(T--) {
        i++;
        printf("Case #%d:\n", i);
        solve();    
    }

    return 0;
}

三元组

假设以三元组(F,C,L/R)的形式输入一棵二叉树的诸边（其中F表示双亲结点的标识，C标识孩子结点的标识，L/R标识C为F的左孩子或右孩子），且在输入的三元组序列中，C是按层次顺序出现的。设结点的标识是字符类型。F=^时C为根节点标识，若C也为^，则标识输入结束。试编写算法，由输入的三元组序列建立二叉树的二叉链表。

输入格式

输入为若干行，每行分别为三个字符，描述如题。

输出格式

输出共一行，为该二叉树的广义表达式。

样例输入复制

^AL
ABL
ACR
^^L

样例输出复制

A(B,C)

#include 
#include 
#include 

const int maxn = 1e4;

typedef struct node {
    char ch;
    struct node *left, *right;
} node;

node *getNewNode(char ch) {
    node *p = (node*)malloc(sizeof(node));
    p->ch = ch;
    p->left = p->right = NULL;
    return p;
}

char str[maxn];
node *arr[26];

void output(node *root) {
    if(root == NULL) return ;
    printf("%c", root->ch);
    
    if(root->left == NULL && root->right == NULL) return ;
    printf("(");
    output(root->left);
    if(root->right) {
        printf(",");
        output(root->right);
    }
    printf(")");
}

int main() {
    
    node *root = NULL, *p;
    while(scanf("%s", str)) {
        if(str[0] == '^' && str[1] == '^') break;
        p = getNewNode(str[1]);
        arr[str[1] - 'A'] = p;  //按层次顺序出现的，孩子结点  
        if(str[0] == '^') {
            root = p;
            continue;
        }
        
        switch(str[2]) {
            case 'L' : arr[str[0] - 'A']->left = p; break;
            case 'R' : arr[str[0] - 'A']->right = p; break;
        }
    }

    output(root);
    printf("\n"); 
    return 0;
}

兔子与兔子

字符串哈希

H = (Σci * base) % mod [0 ~ mod] mod 1e9 + 10

#include 
#include 
#include 

const int maxn = 1e6 + 10;
const int base = 131;
const int mod = 1e9 + 10;

char str[maxn];
long long h[maxn], sum[maxn];

int main() {
    scanf("%s", str + 1);
    int n;
    scanf("%d", &n);
    sum[0] = 1;

    for (int i = 1; str[i]; i++) {
        h[i] = (h[i - 1] * base) + (str[i] - 'a' + 1);
        sum[i] = sum[i - 1] * base ;
    }

    for (int i = 0; i < n; i++) {
        int l1, r1, l2, r2;
        scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
        long long a = h[r1] - h[l1 - 1] * sum[r1 - l1 + 1];
        long long b = h[r2] - h[l2 - 1] * sum[r2 - l2 + 1];
        if (a == b ) { //防止前缀冲突，在乘上一个值
            printf("Yes\n");
        }
        else {
            printf("No\n");
        }
    }



    return 0;
}

最短路算法

Dijkstra算法

算法步骤:
1、初始化集合{S=点集}与{T=空集}
2、从S中选出一个距离点v最近的点n
3、将n加入T中，并从S中删除
4、更新S中所有点距离点v的距离
5、重复2-3- 4，直到S变成空集
时间复杂度:O(N2)
堆优化后:O(N*Log (N) +E)

稀疏图：邻接表

0x3f

代码展示

#include 
#include 
#include 
#include 

using namespace std;

const int maxn = 1e4;
const int inf = 0x3f3f3f3f;

struct node {
    int to, w;
} tmp;
vector w[maxn]; // 二维数组

int vis[maxn], dis[maxn]; 
int n, m, c;

void dij(int c) {
    // 初始化所有点到起点的距离是无穷大
    memset(dis, 0x3f, sizeof(dis));    //赋值为无穷大 
    dis[c] = 0;
    
    // i 循环, 找到一个s集合中的并且离起点最近的点
    for(int i = 1; i <= n; i++) {
        int v = -1, minn = inf;

        // j 循环, 就是找到那个点
        for(int j = 1; j <= n; j++) {
            if(!vis[j] && minn > dis[j]) { //vis[j]为0，没被用过
                v = j;
                minn = dis[j];
            }   
        }
        if(v == -1) {
            return ;
        }
        vis[v] = 1;
        
        // 松弛操作, 看看是直接到这个点更近, 还是绕一下更近
        for(int j = 0; j < w[v].size(); j++) {//  w[v]——所有到v的点
            int k = w[v][j].to;//
            if(!vis[k] && dis[k] > dis[v] + w[v][j].w) {
                dis[k] = dis[v] + w[v][j].w;
            }
        }
    }
    return ;
}

int main() {
    cin >> n >> m >> c;
    for(int i = 0; i < m; i++) {
        int x, y;
        cin >> x >> y;
        tmp.to = y, tmp.w = 1;
        w[x].push_back(tmp);  //  x->y  该成员函数的功能是在 vector 容器尾部添加一个元素
        tmp.to = x;
        w[y].push_back(tmp);  //  y->x
    }
    
    dij(c);

    for(int i = 1; i <= n; i++) {
        cout << dis[i] << endl;
    }

    return 0;
}

用堆进行优化

#include 
#include 
#include 
#include 
#include 
using namespace std;

const int maxn = 1e4;
const int inf = 0x3f3f3f3f;

struct node {
    int to, w;
    bool operator < (const node &a) const {
        return w > a.w;
    }
} tmp;
vector w[maxn];

int vis[maxn], dis[maxn]; 
int n, m, c;

void dij(int c) {  //O(logN + E)
    priority_queue que;
    memset(dis, 0x3f, sizeof(dis));
    dis[c] = 0;
    node temp;
    temp.w = 0;
    temp.to = c;
    que.push(temp); //起点 入队列
    
    while(!que.empty()) { //用优先队列找离起点最近的点
        node head = que.top();        
        que.pop();
        
        int k = head.to;
        
        for(int i = 0; i < w[k].size(); i++) {//更新
            int x = dis[k] + w[k][i].w;
            if(dis[w[k][i].to] > x) {//直接距离和间接距离的比较
                dis[w[k][i].to] = x;
                temp.to = w[k][i].to;
                temp.w = dis[w[k][i].to];
                que.push(temp);//更新的距离放入优先队列
            }
        }
    }
    return ;
}

int main() {
    cin >> n >> m >> c;
    for(int i = 0; i < m; i++) {
        int x, y;
        cin >> x >> y;
        tmp.to = y, tmp.w = 1;
        w[x].push_back(tmp);
        tmp.to = x;
        w[y].push_back(tmp);
    }
    
    dij(c);

    for(int i = 1; i <= n; i++) {
        cout << dis[i] << endl;
    }

    return 0;
}

实现str()

class Solution {
public:
    int strStr(string haystack, string str) {
        int ind[128];
        for (int i = 0; i < 128; i++) ind[i] = str.size();
        for (int i = 0; str[i]; i++) {
            ind[str[i]] = str.size() - i;
        }
        int i = 0;
        while (i + str.size() <= haystack.size()) {
            int flag = 1;
            for (int j = 0; str[j]; j++) {
                if (haystack[i + j] == str[j]) continue;
                flag = 0;
                break;                
            }
            if (flag == 1) return i;
            i += ind[haystack[i + str.size()]];
        }
        return -1;
    }
};

红黑树

五个条件

1. 节点非黑既红
2. 根节点是黑色
3. 叶子（NIL）结点是黑色
4. 红色节点下面接两个黑色节点
5. 从根节点到叶子结点路径上，黑色节点数量相同

最长的长度等于最短长度的2倍

非黑即红，根黑叶黑
红下两黑，路径黑同

1、插入调整站在祖父节点看 （往上回溯，向下看）

2、删除调整站在父节点看 （往上回溯，向下看）

3、插入和删除的情况处理一共总结为五种

插入调整策略（祖父节点）

当前节点下两红的情况

新插入节点是红色    (插入黑色一定造成失衡，插入红色不一定造成失衡(仅当父节点为红色))
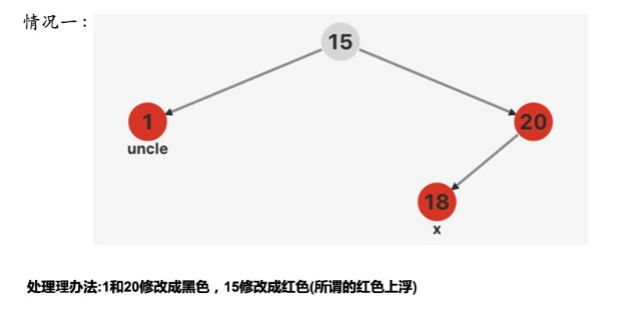
插入操作干掉双红节点

调正操作   双红节点 -> 红黑黑   每条路径黑数量不变 （红色上浮）



1、插入调整站在**祖父节点**看  （往上回溯，向下看）

2、**每次调整后，黑色节点数量保持不变

当前节点下一红一黑的情况

(LR 小左旋) = LL 先大右旋，双红节点->红黑黑/黑红红

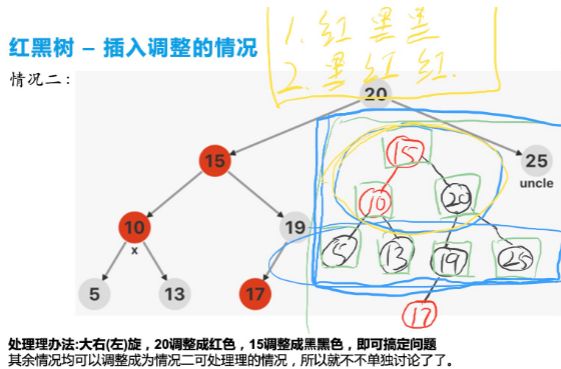
总结/代码

一、平衡条件

1. 节点非黑既红
2. 根节点是黑色
3. 叶子（NIL）结点是黑色
4. 红色节点下面接两个黑色节点
5. 从根节点到叶子结点路径上，黑色节点数量相同

平衡条件的认识
第4条和第5条条件，注定了，红黑树中最⻓路径是最短路径的⻓度的 2 倍。
本质上，红黑树也是通过树高来控制平衡的。红黑树比 AVL 树树高控制条件要更松散，红黑树在发生节点插入和删除以后，发生调整的概率，比 AVL 树要更小。

二、学习诀窍

1. 理解红黑树的插入调整，要站在 祖父节点 向下进行调整
2. 理解红黑树的删除调整，要站在父节点向下进行调整
3. 插入调整，主要就是为了解决双红情况
4. 新插入的节点一定是红色，插入黑色节点一定会产生冲突，违反条件
5. 插入红色节点，不一定产生冲突5. 把每一种情况，想象成一棵大的红黑树中的局部子树6. 局部调整的时候，为了不影响全局，调整前后的路径上黑色节点数量相同

三、插入策略

1. 叔叔节点为红色的时候，修改三元组小帽子，改成红黑黑
2. 叔叔节点为黑色的时候，参考 AVL 树的失衡情况，分成 $LL,LR,RL,RR$, 先参考 AVL 树的旋转调整策略，然后再修改三元组的颜色，有两种调整策略：红色上浮，红色下沉。3.
3. 两大类情况，包含 8 种小情况

#include 
#include 
#include 
#include 

typedef struct Node {
    int key, color; // 0 red, 1 black
    struct Node *lchild, *rchild;
} Node;

Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void inid_NIL() {
    NIL->key = -1;
    NIL->color = 1;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}

Node *getNewNode(int key) { // 插入节点为红色
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->color = 0;
    p->lchild = p->rchild = NIL;
    return p;
}

void clear(Node *root) {
    if(root == NIL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

bool has_red_child(Node *root) {
    return (root->lchild->color == 0 || root->rchild->color == 0);
}

Node *left_rotate(Node *root) {
    printf("left_rotate :%d \n", root->key);
    Node *temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    return temp;
}

Node *right_rotate(Node *root) {
    printf("right_rotate :%d \n", root->key);
    Node *temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    return temp;

}

const char *insert_maintain_str[] = {"", "LL", "LR", "RL", "RR"};

Node *insert_maintain(Node *root) {
    
    if(!has_red_child(root)) {//无红色孩子节点  终止
        return root;
    }
    
    if(root->lchild->color == 0 && root->rchild->color == 0) {//两个红色孩子节点
        if(!has_red_child(root->lchild) && !has_red_child(root->rchild)) {//非双红 终止
            return root;
        }
        // 插入调整, 情况1, 红黑黑
        printf("situation 1 : \n");
        root->color = 0; //红色上浮
        root->lchild->color = root->rchild->color = 1;
        return root;
    }
    // root 下面一个红色，一个黑色，如果是，进去看看有没有冲突，否则返回
    if(root->lchild->color == 0 && !has_red_child(root->lchild)) return root;//儿子节点是红色，孙子节点是黑色， 终止
    if(root->rchild->color == 0 && !has_red_child(root->rchild)) return root;//儿子节点是红色，孙子节点是黑色， 终止
    
    int flag = 0;
    printf("situation 2 : \n");
    if(root->lchild->color == 0) {
        if(root->lchild->rchild->color == 0) {//左子树的右子树是红色
            // LR 先小左旋
            root->lchild = left_rotate(root->lchild);
            flag = 2;
        } else { flag = 1; }
        root = right_rotate(root); //大右旋转
    } else {
        if(root->rchild->lchild->color == 0) {
            // RL 先小右旋
            root->rchild = right_rotate(root->rchild);
            flag = 3;
        } else { flag = 4; }
        root = left_rotate(root); //大左旋
    }

    printf("maintain type : %s\n", insert_maintain_str[flag]);
    
    //调整小三角，红黑黑
    root->color = 0;
    root->lchild->color = root->rchild->color = 1;

    return root;
}

Node *__insert(Node *root, int key) {
    if(root == NIL) return getNewNode(key);
    if(root->key == key) return root;
    if(root->key > key) {
        root->lchild = __insert(root->lchild, key);
    } else {
        root->rchild = __insert(root->rchild, key);
    }
    return insert_maintain(root);//平衡调正操作
}

Node *insert(Node *root, int key) {//分两部走，根节点可能会变，强制改成黑色节点
    root = __insert(root, key);
    root->color = 1;
    return root;
}


void output(Node *root) {
    if(root == NIL) return ;
    printf("(%d | %d, %d, %d) \n", 
          root->color, root->key, root->lchild->key, root->rchild->key);
    output(root->lchild);
    output(root->rchild);
    return ;
}

int main() {
    int n;
    Node *root = NIL;
    scanf("%d", &n);
    for(int i = 0; i < n; i++) {
        int val = rand() % 100;
        printf("\n insert %d to RB_tree : \n",  val);
        root = insert(root, val);
        output(root);
    }
    clear(root);
    return 0;
}

删除的前提︰
1．删除红色节点（度为1不可能，路径长度不同）
a.度为0
b.度为2
2．删除黑色节点
a.度为2
b.度为1（度为1子节点一定是红色，红色变黑色，子节点是黑色不可能，路径长度不同）
c.度为0 （暂时引入双重黑节点，暂时平衡）

一、删除调整发生的前提

1. 删除红色节点，不会对红黑树的平衡产生影响
2. 度为1的黑色节点，唯一子孩子，一定是红色
3. 删除度为1的黑色节点，不会产生删除旋转调整
4. 删除度为0的黑色节点，会产生一个双重黑的 NIL 节点
5. 删除调整，就是为了干掉双重

双重黑色节点（有向上传递的性质）

删除调整策略（父节点）

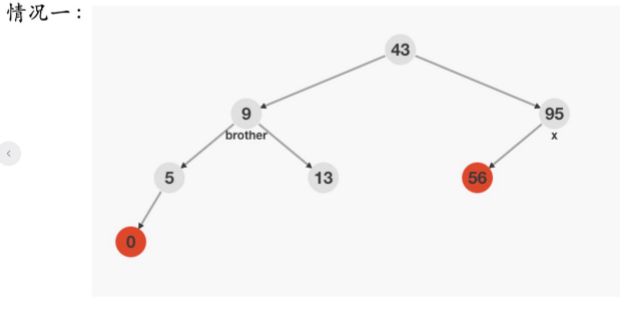
情况一：双重黑节点的兄弟节点是黑色，兄弟节点下面的两个子节点也是黑色

处理办法：父节点增加一重黑色，双重黑与兄弟节点，分别减少一重黑色（黑色向上传递）

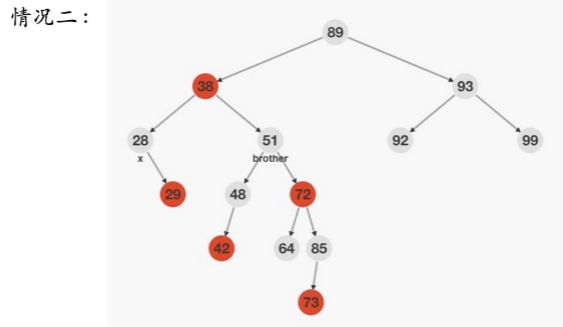
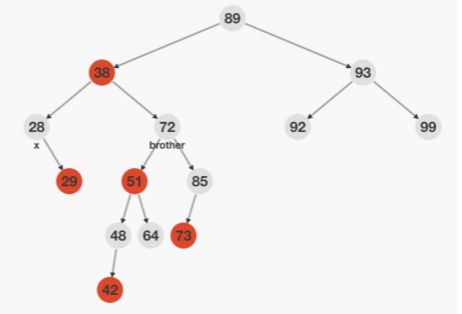
情况二：双重黑节点的兄弟节点是黑色，兄弟节同一侧的子节点是红色

下图为RR型失衡 大左旋

处理办法: father左(右)旋，由于无法确定48的颜色，所以38改成黑色，51改成38的颜色，×减少一重黑色，72改成黑色

让另一侧的黑色节点数量减一，同侧黑色节点数量加一，
1、38为黑色，左旋异侧减一，同侧加一
2、38为红色，左旋异侧不变，同侧加一，将38变为黑色，51变为红色，异侧减一
同侧加一，消去双重黑即可平衡，
异侧减一，将原来兄弟节同一侧的子节点变为黑色即可平衡。

51和38颜色对换保证异侧黑色节点数量一定减一，故将原来兄弟节同一侧的子节点变成红色即可保持平衡

情况三：

RR类型优先即大于RL类型

双重黑节点的兄弟节点是黑色，兄弟节同一侧的子节点是黑色，异侧节点为红色
下图为RL型失衡 小右旋 变为RR型失衡

处理办法: brother右(左)旋，51变黑，72变红，转成处理情况二

情况四：
X的兄弟节点是红色怎么办？

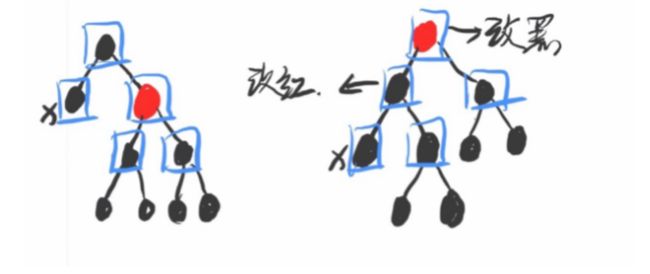
左旋，交换原父节点和原兄弟节点颜色

代码演示

1. 进行 LR/RL 类型判断的时候，不能判断 LL 子树是否为黑色，LL 子树有可能是 NIL 节点，在某些特殊情况下，读到的颜色可能是双重黑，取而代之的判断方法就是【LL 子树不是红色】。

#include 
#include 
#include 
#include 

typedef struct Node {
    int key, color; // 0 red, 1 black, 2 double black
    struct Node *lchild, *rchild;
} Node;

Node __NIL;
#define NIL (&__NIL)
__attribute__((constructor))
void inid_NIL() {
    NIL->key = -1;
    NIL->color = 1;
    NIL->lchild = NIL->rchild = NIL;
    return ;
}

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->color = 0;
    p->lchild = p->rchild = NIL;
    return p;
}

void clear(Node *root) {
    if(root == NIL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

bool has_red_child(Node *root) {
    return (root->lchild->color == 0 || root->rchild->color == 0);
}

Node *left_rotate(Node *root) {
    printf("left_rotate :%d \n", root->key);
    Node *temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    return temp;
}

Node *right_rotate(Node *root) {
    printf("right_rotate :%d \n", root->key);
    Node *temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    return temp;

}

const char *insert_maintain_str[] = {"", "LL", "LR", "RL", "RR"};

Node *insert_maintain(Node *root) {
    if(!has_red_child(root)) {
        return root;
    }
    if(root->lchild->color == 0 && root->rchild->color == 0) {
        if(!has_red_child(root->lchild) && !has_red_child(root->rchild)) {
            return root;
        }
        // 插入调整, 情况1, 红黑黑
        printf("situation 1 : \n");
        root->color = 0;
        root->lchild->color = root->rchild->color = 1;
        return root;
    }
    if(root->lchild->color == 0 && !has_red_child(root->lchild)) return root;
    if(root->rchild->color == 0 && !has_red_child(root->rchild)) return root;
    
    int flag = 0;
    printf("situation 2 : \n");
    if(root->lchild->color == 0) {
        if(root->lchild->rchild->color == 0) {
            // LR 先左旋
            root->lchild = left_rotate(root->lchild);
            flag = 2;
        } else { flag = 1; }
        root = right_rotate(root);
    } else {
        if(root->rchild->lchild->color == 0) {
            // RL 先右旋
            root->rchild = right_rotate(root->rchild);
            flag = 3;
        } else { flag = 4; }
        root = left_rotate(root);
    }

    printf("maintain type : %s\n", insert_maintain_str[flag]);
    root->color = 0;
    root->lchild->color = root->rchild->color = 1;

    return root;
}

Node *__insert(Node *root, int key) {
    if(root == NIL) return getNewNode(key);
    if(root->key == key) return root;
    if(root->key > key) {
        root->lchild = __insert(root->lchild, key);
    } else {
        root->rchild = __insert(root->rchild, key);
    }
    return insert_maintain(root);
}

Node *insert(Node *root, int key) {
    root = __insert(root, key);
    root->color = 1;
    return root;
}

Node *get_pre(Node *root) {
    Node *temp = root->lchild;
    while(temp->rchild != NIL) temp = temp->rchild;
    return temp;
}

Node *erase_maintain(Node *root) {
    // 站在父节点, 看看两个孩子没有有双重黑色
    if(root->lchild->color != 2 && root->rchild->color != 2) {
        return root;
    }
    // 先处理一个双黑一个红色  
	//情况四、右红则左旋，交换原父节点和原兄弟节点颜色
    if(has_red_child(root)) {
        int flag = 0; // flag 是记一下, 红色节点在哪里
        // 先让原来的老根, 变成红色
        root->color = 0;
        if(root->lchild->color == 0) {
            root = right_rotate(root); //右旋
            flag = 1;
        } else {
            root = left_rotate(root);  //左旋
            flag = 2;
        }
        root->color = 1;
        if(flag == 1) root->rchild = erase_maintain(root->rchild);
        else root->lchild = erase_maintain(root->lchild);
        return root;
    }
    
    // 情况1, 兄弟节点的两个孩子也是双黑      双黑向上传递
    if((root->lchild->color == 2 && !has_red_child(root->rchild))
    || (root->rchild->color == 2 && !has_red_child(root->lchild))) {
        root->lchild->color -= 1;
        root->rchild->color -= 1;
        root->color += 1;
        return root;
    }
    
    // 情况2和情况3的处理
    // 当左节点是双黑的时候   向黑色节点旋转
    if(root->lchild->color == 2) {
        // 减掉双黑的一重黑色
        root->lchild->color = 1;
        // RL
        if(root->rchild->rchild->color != 0) {
            // RL 需要先进行一次小右旋, 原根变红, 新根边黑
            root->rchild->color = 0;
            root->rchild = right_rotate(root->rchild);
            root->rchild->color = 1;
        }
        // RR
        root = left_rotate(root);
        root->color = root->lchild->color;
    } else {
        root->rchild->color = 1;
        // LR
        if(root->lchild->lchild->color != 0) {
            // LR 需要先进行一次小左旋, 原根变红, 新根边黑
            root->lchild->color = 0;
            root->lchild = left_rotate(root->lchild);
            root->lchild->color = 1;
        }
        // LL
        root = right_rotate(root);
        root->color = root->rchild->color;
    }
    root->lchild->color = root->rchild->color = 1;
    return root;
}

Node *__erase(Node *root, int key) {
    if(root == NIL) return NIL;
    if(root->key > key) {
        root->lchild = __erase(root->lchild, key);
    } else if(root->key < key) {
        root->rchild = __erase(root->rchild, key);
    } else {
        // 处理度为0或者度为1
        if(root->lchild == NIL || root->rchild == NIL) {
            Node *temp = root->lchild != NIL ? root->lchild : root->rchild;
            temp->color += root->color; //
            free(root);
            return temp;
        } else {
            //处理度为二的节点
            Node *temp = get_pre(root);
            root->key = temp->key;//找前驱节点覆给root，删除前驱节点，转换为度为1或2的情况
            root->lchild = __erase(root->lchild, temp->key);
        }
    }
    return erase_maintain(root);
}

Node *erase(Node *root, int key) {
    root = __erase(root, key);
    root->color = 1;
    return root;
}


void output(Node *root) {
    if(root == NIL) return ;
    printf("(%d | %d, %d, %d) \n", 
          root->color, root->key, root->lchild->key, root->rchild->key);
    output(root->lchild);
    output(root->rchild);
    return ;
}

int main() {
    int n;
    Node *root = NIL;
    
    int op, val;

    while(~scanf("%d%d", &op, &val)) {
        switch(op) {
            case 1 : root = insert(root, val); break;
            case 2 : root = erase(root, val); break;
        }
        output(root);
        printf("---------------------\n");
    }
    clear(root);
    return 0;
}

海贼红黑树

哈夫曼编码

定长与变长编码
1.Ascii编码和特定场景下的自定义编码，都属于定长编码
2.对于每一个字符，编码长度相同，这就是定长编码
3.UTF-8编码，是变长编码，UTF-16，是定长编码
4.对于每一个字符，编码长度不相同，这就是变长编码

前缀编码可以保证对压缩文件进行解码时不产生二义性，确保正确解码。
哈夫曼编码符合“前缀编码”的要求，即较短的编码不能是任何较长的编码的前缀。

哈夫曼编码生成过程:
1.首先，统计得到每一种字符的概率
2.将n 个字符，建立成一棵哈弗曼树
概率最小的放下面，每一个节点放在叶子节点
3.每一个字符，都落在叶子结点上
4.按照左0，右1的形式，将编码读取出来

结论:哈弗曼编码，是最优的变长编码

1. 首先表示平均编码⻓度，求解公式最优解

2. 最终，和熵与交叉熵之间的关系

2^(H-L) 代表编码长度为L的使用了多少个节点

代码演示

#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

typedef struct Node {
    char ch;
    double freq;
    struct Node *lchild, *rchild;
} Node;

struct cmp {
    bool operator() (const Node *a, const Node *b) {
        return a->freq > b->freq;
    }
};

priority_queue, cmp> q;  //存Node的优先队列

Node *getNewNode(char ch, double freq, Node *lchild, Node *rchild) {
    Node *p = (Node*)malloc(sizeof(Node));
    p->ch = ch;
    p->freq = freq;
    p->lchild = lchild;
    p->rchild = rchild;
    return p;
}

void clear(Node *root) {
    if(root == NULL) return ;
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

Node *buildHalfmman() {
    while(!q.empty()) {
        Node *a = q.top();
        q.pop();
        Node *b = q.top();
        q.pop();
        q.push(getNewNode(0, a->freq + b->freq, a, b));
    }
    return q.top();
}

void getHalfmmanCode(Node *root, int k, char *buff, char *code[]) { //k是第几个，buff是单个编码， code[]是连续的编码
    if(root == NULL) return ;
    buff[k] = 0;
    if(root->ch) {
        code[root->ch] = strdup(buff);
        return ;
    }
    buff[k] = '0';
    getHalfmmanCode(root->lchild, k + 1, buff, code);	//递归遍历
    buff[k] = '1';
    getHalfmmanCode(root->rchild, k + 1, buff, code);
    return ;
}

int main() {
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; i++) {
        char ch[10];
        double freq;
        scanf("%s%lf", ch, &freq);
        q.push(getNewNode(ch[0], freq, NULL, NULL));
    }
    Node *root = buildHalfmman();
    char *code[256] = {0}, buff[100];
    
    getHalfmmanCode(root, 0, buff, code);

    for(int i = 1; i < 256; i++) {
        if(code[i] == NULL) continue;
        printf("%c : %s\n", i, code[i]);
    }

    return 0;
}

刷题

LRU 缓存机制

struct DlinkNode { //双向链表
    int key, value;
    DlinkNode *next, *pre;
    DlinkNode() : key(0), value(0), next(nullptr), pre(nullptr) {}
    DlinkNode(int _key, int _value) : key(_key), value(_value), next(nullptr), pre(nullptr) {}
};
class LRUCache {    
public:
    unordered_map<int, DlinkNode*> hash;
    DlinkNode *head, *tail;
    int size, m_capacity;//  size当前大小，m_capacity最大容量
    LRUCache(int capacity) {
        m_capacity = capacity;
        head = new DlinkNode();
        tail = new DlinkNode();
        head->next = tail;
        tail->pre = head;
        size = 0;
    }
    
    int get(int key) {
        if(!hash.count(key)) {
            return -1;
        }
        move_head(key);//放在头部
        return hash[key]->value;
    }

    void move_head(int key) {
        DlinkNode *node = hash[key];
        node->pre->next = node->next;
        node->next->pre = node->pre;

        head->next->pre = node;
        node->next = head->next;
        head->next = node;
        node->pre = head;
        return ;
    }
    
    void add_node(DlinkNode *node) {
        head->next->pre = node;
        node->next = head->next;
        node->pre = head;
        head->next = node;
        return ;
    }

    void delete_node() {
        DlinkNode *node = tail->pre;
        int key = node->key;
        tail->pre = node->pre;
        node->pre->next = tail;
        hash.erase(key);
        delete node;
        return ;
    }

    void put(int key, int value) {
        if(!hash.count(key)) {
            if(size >= m_capacity) {
                delete_node();
                size--;
            }
            DlinkNode *node = new DlinkNode(key, value);
            add_node(node);
            size++;
            hash[key] = node;
        } else {
            DlinkNode *node = hash[key];
            node->value = value;
            move_head(key);
        }
        return ;
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

古老打字机

蒜头君有一台古老的打印机，在打印机上有 2828个按键，其中：

a - z：输入一个小写英文字母；

DEL：删除当前输入的单词的最后一个字母；

PRINT：打印当前输入的单词。

蒜头君想使用这台打印机打印出 nn 个英文单词，打印单词的顺序无所谓。求蒜头君最少需要按多少次按钮。

输入格式

输入包含多组测试数据，对于每组测试数据：

第一行输入一个整数 nn（1 \leq n \leq 100001≤n≤10000），表示一共需要打印的单词数。

接下来输入 nn 行，每行输入一个单词，每个单词的长度不超过 5050，并且只包含小写英文字母。

输出格式

对于每组测试数据，输出一个整数，表示打印出这些单词，蒜头君最少需要按的按钮次数。

样例输入复制

3
apple
add
oppo

样例输出复制

20

代码

#include 
#include 
#include 

typedef struct Node {
    struct Node* next[26];
} Node;
int count = 0;

Node *getNewNode() {
    Node *p = (Node*)malloc(sizeof(Node));
    memset(p->next, 0, sizeof(p->next));
    return p;
}

void insert(Node *root, char *str) {
    Node *p = root;
    for(int i = 0; str[i]; i++) {
        if(p->next[str[i] - 'a'] == NULL) {
            p->next[str[i] - 'a'] = getNewNode();
            count++;
        }
        p = p->next[str[i] - 'a'];
    }
    return ;
}

int main() {
    int n;
    while(scanf("%d", &n) != EOF) {
        count = 0;
        Node *root = getNewNode();    
        char str[512];
        int max_len = 0, len;
        for(int i = 0; i < n; i++) {
            scanf("%s", str);
            len = strlen(str);
            max_len = max_len < len ? len : max_len;
            insert(root, str);
        }
        int ans = count * 2 + n - max_len;
        printf("%d\n", ans);   
    }
    return 0;
}

字符串旋转矩阵

已知一个字符串 ss，例如hello，在其末尾添加一个结束符$， 然后对其进行 nn 次旋转，其中 nn 为字符串 ss 的长度，于是一共得到了 n+1n+1个字符串，例如对于字符串hello得到：

1

hello$

2

ello$h

3

llo$he

4

lo$hel

5

o$hell

6

$hello

然后对这 n+1n+1 个字符串按照字典序排序，得到一个字符矩阵：

1

$hello

2

ello$h

3

hello$

4

llo$he

5

lo$hel

6

o$hell

对于该字符矩阵的最后一列，由上到下得到一个字符串 TT =oh$ell。

现在已知字符串 TT，有 mm 次询问，求字符串 strstr 是否是原字符串 ss 的子串。

输入格式

输入包含多组测试数据，对于每组测试数据：

第一行包含一个字符串 T(1 \leq |T| \leq 110000)T(1≤∣T∣≤110000)，字符串 TT 中只包含小写英文字母和一个$。

第二行包含一个整数 m (m \leq 110000)m(m≤110000)。

接下来 mm 行每行包含一个字符串 strstr（|str| \times m \leq 2 \times 10^{6}∣str∣×m≤2×106)，字符串 strstr 中只包含小写英文字母。

输出格式

对于每组测试数据的每次询问，输出一个结果，如果该字符串是原字符串 ss 的子串，输出YES，否则输出NO。

注意： 本题难度较大，为选做题，提交任意一份代码就可以跳过这一节。

样例输入复制

oh$ell
3
hel
ho
ele

样例输出复制

YES
NO
NO

代码

#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

const int maxn = 210000;
char s[maxn], t[maxn];
int ind[maxn];

bool cmp(int i, int j) {
    if (t[i] != t[j]) return t[i] < t[j];
    return i < j;
}

void conver(char *t, char *s) {
    int n = 0;
    for (n = 0; t[n]; n++) {
        ind[n] = n;
    }
    sort(ind, ind + n, cmp);
    /*for (int i = 0; i < n; i++) {//排完序后下标的值，第一列
        printf("%d", ind[i]);
    }*/
    
    int p = ind[0];
    for (int i = 0; i < n; i++) {
        s[i] = t[p];
        p = ind[p];
    }
    s[n] = '\0';
    return ;
}

const int maxm = 2e6 + 10;

int *ans[maxn];
struct Node {
    int flag, *ans;
    int next[26], fail;
} tree[maxm];
int root = 1, cnt = 2;

int getNewNode() {return cnt++;}

int *insert(char *s) {
    int p = root;
    for (int i = 0; s[i]; i++) {
        int ind = s[i] - 'a';
        if (tree[p].next[ind] == 0) tree[p].next[ind] = getNewNode();
        p = tree[p].next[ind];
    }
    tree[p].flag = 1;
    if (tree[p].ans == NULL) {
        tree[p].ans = new int(0);
    }
    return tree[p].ans;
}

void build() {
    queue que;
    tree[root].fail = 0;
    for (int i = 0; i < 26; i++) {
        if (tree[root].next[i] == 0) {
            tree[root].next[i] = root;
            continue;
        }
        tree[tree[root].next[i]].fail = root;
        que.push(tree[root].next[i]);
    }
    
    while(!que.empty()) {
        int p = que.front();
        que.pop();
        
        for (int i = 0; i < 26; i++) {
            int c = tree[p].next[i], k = tree[p].fail;
            if (c == 0) {
                tree[p].next[i] = tree[k].next[i];
                continue;
            }
            tree[c].fail = tree[k].next[i];
            que.push(c);
        }
    }
    return ;
}

void match(char *s) {
    int ind = s[0] - 'a';
    int p = tree[root].next[ind], q, k;
    for (int i = 0; s[i]; i++, p = tree[p].next[s[i] - 'a']) {
        q = p;
        while (q) {
            if (tree[q].flag) {
                *tree[q].ans += 1;
            }
            k = q;
            q = tree[q].fail;
            tree[k].fail = 0;
            
            
        }
    }
}

int solve(char *t) {
    memset(ans, 0, sizeof(ans));
    memset(tree, 0, sizeof(tree));
    cnt = 2;

    conver(t, s);
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%s", t);
        ans[i] = insert(t); //tree[p].ans   同名
    }
    build();
    match(s + 1);//把$丢掉
    
    for (int i = 0; i < n; i++) {
        if (ans[i][0]) {
            printf("YES\n");
        } else {
            printf("NO\n");
        }
    }
    return 0;
}

int main() {
   while (scanf("%s", &t) != EOF) {
       solve(t);
   }
    
    return 0;
}

二叉搜索树的最近公共祖先

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		
        if (p->val < root->val && q->val < root->val) {
            return lowestCommonAncestor(root->left, p, q);
        }
        if (p->val > root->val && q->val > root->val) {
            return lowestCommonAncestor(root->right, p, q);
        }
        return root;
    }
};

路径总和

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetsum){
        if (root == nullptr) return false;
        if (root->left == nullptr && root->right == nullptr){// 叶子结点
            return targetsum == root->val;
        }
        targetsum -= root->val;
        return  hasPathSum(root->left, targetsum) || hasPathSum(root->right, targetsum);
    }
};

二叉树中的最大路径和（巧妙）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = -0x3f3f3f3f;

    int dfs(TreeNode *root) {
        if (root == nullptr) return 0;
        int left = max(0, dfs(root->left));
        int right = max(0, dfs(root->right));
        ans = max(ans, left + right + root->val);
        return root->val + max(left, right);
    }

    int maxPathSum(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

不同的二叉搜索树

class Solution {
public:
    int mp[200][200] = {0};
    int dfs(int l, int r) { // l号结点  到 n号结点
        if (l > r) return 1;  //边界条件
        if (mp[l][r] != 0) return mp[l][r];
        int res;
        for (int i = l;i <= r; i++) {
            res += (dfs(l, i - 1) * dfs(i + 1, r));
        }
        mp[l][r] = res;
        return res;
    }

    int numTrees(int n) {
        if (n == 1) return 1;
        return dfs(1, n);
    }
};

不同的二叉搜索树 II（排列组合）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    
    vector dfs(int l, int r) {
        vector ans;
        if (l > r) { // 边界条件
            ans.push_back(nullptr);
            return ans;
        }

        for (int i = l; i <= r; i++) {
            vector left_arr = dfs(l, i - 1);
            vector right_arr = dfs (i + 1, r);
            
            for (TreeNode *left : left_arr) { // 遍历整个树，排列组合
                for (TreeNode *right : right_arr) {
                    TreeNode *t = new TreeNode(i, left, right);
                    ans.push_back(t);
                }
            }
        }
        return ans;
    }

    vector generateTrees(int n) {
            if (n == 0) return vector{};
            return dfs(1, n);
    }
};

字串匹配

已知一个字符串 aa 和一个字符串 bb，求字符串 aa 中包含子串 bb 的数量。为了减小输入量，输入中对字符串 aa 进行了压缩，对于字符串 aa 中存在多个连续重复子串，使用方括号括起来，之后一个整数表示该子串连续出现的次数，比如字符串wabababyui可以表示为w[ab]3yui。

输入格式

第一行输入一个字符串 aa，该字符串仅包含小写英文字母、数字和方括号"[]"，长度不超过 10001000，并且不存在括号嵌套的情况。方括号后面的数字不超过 10001000。

第二行包含一个字符串 bb，该字符串仅包含小写英文字母，长度不超过 100100，对于大多数测试数据，字符串 bb 的长度都比较短。

输出格式

对于每组测试数据，输出一个整数，表示字符串 aa 中包含子串 bb 的数量。

样例输入1复制

c[ab]2[da]2da
bd

样例输出1复制

1

样例输入2复制

b[an]3
na

样例输出2复制

2

代码

#include 
#include 
#include 
using namespace std;

const int maxn = 1e6 + 10;
char a[maxn], b[maxn];
char t[maxn];
char tmp[maxn];

void get_string(char *s) {
    int flag = 0, ind = 0, ind_t = 0;
    
    for (int i = 0; s[i]; i++) {
        if(s[i] == '[') {
            flag = 1;
            ind = 0;
        } else if(s[i] == ']') {
            flag = 0;
            tmp[ind] = '\0';
            int x = 0;
            i++;
            while (s[i] <= '9' && s[i] >= '0') {
                x = x * 10 + (s[i] - '0');
                i++;
            }
            i--;
            while (x--) {
                strcat(t, tmp);
                ind_t += ind;
            }
        } else if (flag == 1) { 
          	tmp[ind++] = s[i];
        } else {
            t[ind_t++] = s[i];
        }
    }
    t[ind_t++] = '\0';
    //printf("%s", t);
    return ;
}

void sunday(char *s, char *t) {
    int str_p[3000];
    int len_t = strlen(t);
    int len_s = strlen(s);
    int ans = 0;
    
    for (int i = 0; i < 300; i++) {
        str_p[i] = len_t + 1;
    }
    for (int i = 0; i 

strcat 将两个char类型连接
extern char *strcat(char *dest, const char *src);

strdup（）函数是c语言中常用的一种字符串拷贝库函数，strdup()在内部调用了malloc()为变量分配内存，不需要使用返回的字符串时，需要用free()释放相应的内存空间，否则会造成内存泄漏。