蓝桥杯题目合集一

正文

螺旋折线

题目描述

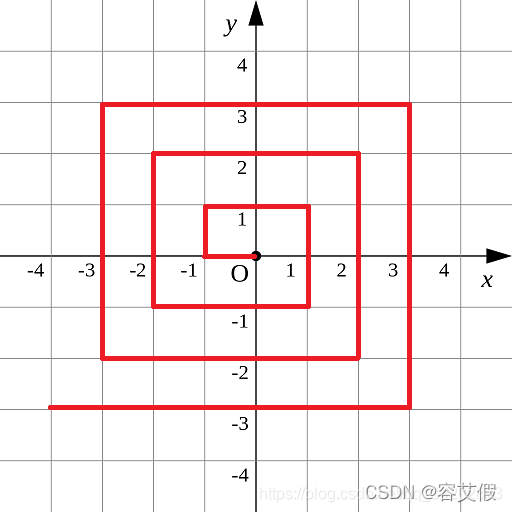
　对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。

　　例如dis(0, 1)=3, dis(-2, -1)=9

　　给出整点坐标(X, Y)，你能计算出dis(X, Y)吗？
输入格式
　　X和Y

　　对于40%的数据，-1000 <= X, Y <= 1000
　　对于70%的数据，-100000 <= X， Y <= 100000
　　对于100%的数据, -1000000000 <= X, Y <= 1000000000
输出格式
　　输出dis(X, Y)
样例输入
0 1
样例输出
3

题目思路及代码

思路：只要找出Y轴上所有点的坐标规律（称之为横向关键点），即求出后与该点所在同一横线上的距离也都可以求出了。

当y > 0 时：
当abs(x) <= y时，dis(0 , y）=3 * y + (y * y - y) / 2  * 8，所以dis(x , y)=dis(0 , y) + x;
当abs(x) > 时, x  > 0时，dis(x , y) = dis(0 , x) + 2 * x - y。
                        x <  0时，dis(x , y) = dis(0 ,-x) + 2 * x + y。 

当y <= 0时：
当y-1 <= x <= -y 时，dis(0 , -y) = 7 * -y + (y * y + y)/2 * 8,所以dis(x , y) =dis(0 , y) - x;
当x >- y 或 x< y - 1时，x > 0 时，dis(x,y) = dis(0 , x) - 2 * x - y。               
					   x < 0 时，dis(x,y) = dis(0 , -x - 1) - 2 * x + y - 1。

代码：

#include
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const ll maxn=1e3+10;
ll x,y;

int main(){
    cin>>x>>y;
    ll n=max(abs(x),abs(y));
    ll dx=-n,dy=-n;
    ll ans=0;
    ans=n*(n-1)*4;
    if(y==-n){
        ans+=3*n*2+n-x;
    }
    if(y==n){
        ans+=2*n+x+n;
    }
    if(x==-n){
        ans+=n+y;
    }
    if(x==n){
        ans+=n*2*2+n-y;
    }
    cout<<ans;
	return 0;
}

最大乘积

题目描述

给定N个整数A1, A2, ... AN。请你从中选出K个数，使其乘积最大。

　　请你求出最大的乘积，由于乘积可能超出整型范围，你只需输出乘积除以1000000009的余数。

　　注意，如果X<0， 我们定义X除以1000000009的余数是负(-X)除以1000000009的余数。
　　即：0-((0-x) % 1000000009)
输入格式
　　第一行包含两个整数N和K。
　　以下N行每行一个整数Ai。

　　对于40%的数据，1 <= K <= N <= 100
　　对于60%的数据，1 <= K <= 1000
　　对于100%的数据，1 <= K <= N <= 100000 -100000 <= Ai <= 100000
输出格式
　　一个整数，表示答案。

样例输入
5 3
-100000
-10000
2
100000
10000
样例输出
999100009

再例如：
样例输入
5 3
-100000
-100000
-2
-100000
-100000
样例输出
-999999829

题目思路及代码

先按照绝对值从大到小排序
①假如选的k个数中必定有0，则结果为0
②假如都是负数，此时若k为偶数，则选前k个数即可，若k为奇数，则只能从小的开始选k个数
③假如都为正数，选前k个数即可
④假如正负都有，此时

• 若前k个数有偶数个负数，则选前k个数即可
• 若前k个数有奇数个负数，则我们看看能不能从后面选一个大正数跟前面的小负数做交换，或者从后面选一个大负数跟前面的小正数做交换，二者取结果大的.
  此时分完所有情况若结果还为负数，我们看看输入是否有0，有零结果即为0，否则就只能输出这个负数了.

代码

#include
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const ll maxn=1e5+10;
const ll mod=1000000009;
ll n;
ll a[maxn];
ll k;
int main(){
    cin>>n>>k;
    for(int i=1;i<=n;i++){
        scanf("%lld",&a[i]);
    }
    sort(a+1,a+1+n);
    if(n==k){
        ll res=1;
        for(int i=1;i<=n;i++){
            res=res*a[i]%mod;
        }
        cout<<res;
        return 0;
    }
    if(a[n]<0){
        if(k&1){
            ll res=1;
            for(int i=n-k+1;i<=n;i++){
                res=res*a[i]%mod;
            }
            cout<<res<<endl;
        }
        else{
            ll res=1;
            for(int i=1;i<=k;i++){
                res=res*a[i]%mod;
            }
            cout<<res<<endl;
        }
        return 0;
    }
    ll l=1,r=n;
    ll res=1;
    if(k&1){
        res=a[r];
        r--;
        k--;
        //if(res<0)sign=-1;
    }
    while(k){
        ll x=(ll)a[r]*a[r-1],y=(ll)a[l]*a[l+1];
        if(x>=y){
            r-=2;
            res=x%mod*res%mod;//先对x进行取模，在对乘积结果进行取模,原因是x也是乘积结果如果不取模乘上的结果不对
        }
        else{
            l+=2;
            res=y%mod*res%mod;//先对y进行取模，在对乘积结果进行取模
        }
        k-=2;
    }

    cout<<res;


	return 0;
}

递增三元组

题目描述

　给定三个整数数组
　　A = [A1, A2, ... AN],
　　B = [B1, B2, ... BN],
　　C = [C1, C2, ... CN]，
　　请你统计有多少个三元组(i, j, k) 满足：
　　1. 1 <= i, j, k <= N
　　2. Ai < Bj < Ck
输入格式
　　第一行包含一个整数N。
　　第二行包含N个整数A1, A2, ... AN。
　　第三行包含N个整数B1, B2, ... BN。
　　第四行包含N个整数C1, C2, ... CN。

　　对于30%的数据，1 <= N <= 100
　　对于60%的数据，1 <= N <= 1000
　　对于100%的数据，1 <= N <= 100000 0 <= Ai, Bi, Ci <= 100000
输出格式
　　一个整数表示答案

样例输入
3
1 1 1
2 2 2
3 3 3
样例输出
27

题目思路及代码

思路：可以先对三个数组排序，然后遍历数组b，查找a数组中有多少个小于b[i]的，c数组中有多少个大于b[i]的

#include
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const ll maxn=1e5+10;
const ll mod=1000000009;
ll n;
ll a[maxn],b[maxn],c[maxn];
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=n;i++){
        cin>>b[i];
    }
    for(int i=1;i<=n;i++){
        cin>>c[i];
    }
    sort(a+1,a+1+n);
    sort(b+1,b+1+n);
    sort(c+1,c+1+n);
    ll sum=0;
    for(int i=1;i<=n;i++){
        ll x=lower_bound(a+1,a+1+n,b[i])-a;
        ll y=upper_bound(c+1,c+1+n,b[i])-c;
        sum=sum+(x-1)*(n-y+1);
        //cout<
    }
    cout<<sum;
	return 0;
}

结语

---

“遇事不决可问春风，春风不语即随本心”的意思是：对一件事犹豫不决，就问春风该如何做，春风给不出答案，就凭自己本心做出决断。“遇事不决可问春风，春风不语即随本心”一句出自网络作家“烽火戏诸侯”的《剑来》，其原文是：“遇事不决，可问春风。春风不语，遵循己心”。

---