参考
3.6 softmax回归的从零开始实现
import torch
import torchvision
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
3.6.1. 获取和读取数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
3.6.2. 初始化模型参数
num_inputs = 784
num_outputs = 10
W = torch.tensor(np.random.normal(0, 0.01, (num_inputs, num_outputs)), dtype=torch.float)
b = torch.zeros(num_outputs, dtype=torch.float)
W.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
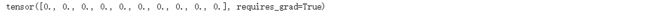
3.6.3. 实现softmax运算
def softmax(X):
X_exp = X.exp()
partition = X_exp.sum(dim=1, keepdim=True)
return X_exp / partition
3.6.4. 定义模型
def net(X):
return softmax(torch.mm(X.view((-1, num_inputs)), W) + b)
3.6.5. 定义损失函数
def cross_entropy(y_hat, y):
return -torch.log(y_hat.gather(1, y.view(-1, 1)))
3.6.6. 计算分类准确率
def accuracy(y_hat, y):
return (y_hat.argmax(dim=1) ==y).float().mean().item()
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum /n
3.6.7. 训练模型
num_epochs, lr = 5, 0.1
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
d2l.sgd(params, lr, batch_size)
else:
optimizer.step()
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size, [W, b], lr)

3.6.8. 预测
X, y = iter(test_iter).next()
true_labels = d2l.get_fashion_mnist_labels(y.numpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])

![]()

