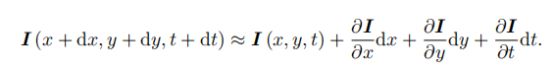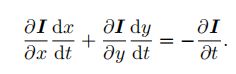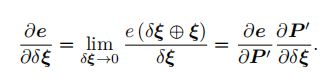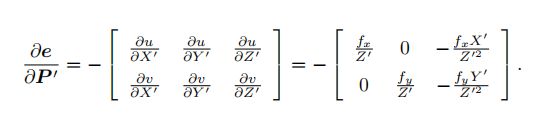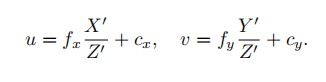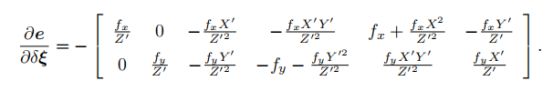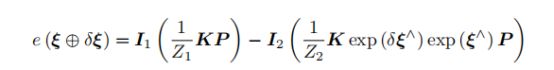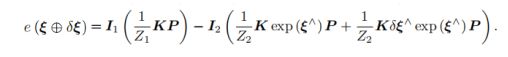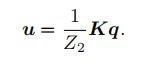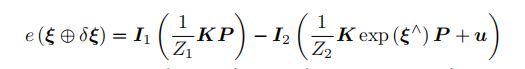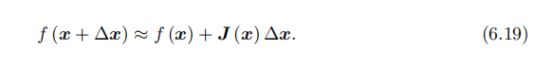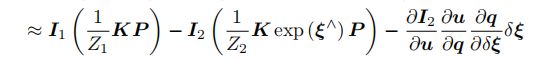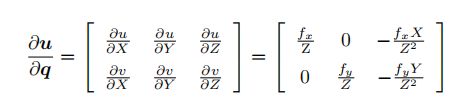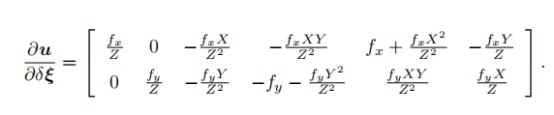SLAM14讲学习笔记（五）视觉里程计（光流法和直接法）和对于雅克比矩阵的理解

这章的内容不多，但是很奇妙的和上一章的串起来了。这里我简单总结一下光流法和直接法，主要想在最后总结和比较一下两个这节和上一节尤其是雅克比矩阵推导上的区别。雅克比矩阵的内容非常关键，如果不能充分理解它们的含义，前端基本就没有办法使用g2o来进行图优化。本文的内容主要是讲述重投影误差和光度误差分别对于位姿求偏导、以及对于世界坐标系下的点求偏导的理论文章，不涉及代码。如果希望理解代码中是如何用到雅克比矩阵的，如何实现的求偏导更新操作，请看我这节的内容：

SLAM14讲学习笔记（十一）g2o图优化中的要点与难点（前端VO中雅克比矩阵的定义）

---

先从大体上总结下：光流法和直接法都是基于一个灰度不变假设，即同一个空间点的像素灰度值在各个图像中是固定不变的。（虽然我感觉这个假设挺扯的，高博在书里也说可能不成立，但是当帧率较快，两张图非常接近的时候，凑合也不能算错）

光流的介绍是为了引出直接法。一个在t时刻位于（x，y）处的像素，在t+dt时刻运动到（x+dx，y+dy）处。两个像素实际是同一个空间点，所以灰度不变。泰勒展开保留一阶项：

基于灰度不变假设，后面的三个偏微分和是0，然后把dt给约掉：

这样，根据图像来说，很直观可以看到的是像素点的灰度关于x，y两个方向的导数（因为像素点是离散的，最小的一格更新量，其实也就是它在下一个图里隔壁点和它灰度的差值，比如202页的那个示例）

dx/dt,dy/dt,这俩就是像素的运动速度，这个是不知道的，是想求的。

等式右边的灰度关于时间的导数，其实也就是对于下一时刻时间的变化量，也是知道的。（两张图像同一个位置的灰度之差）

然后写成矩阵形式，把朝着两个方向的运动速度当成要求解的变量，构造一个线性方程组，然后求解。

假设所有像素都有相同的运动，这样所有的点都套进方程组来，求解最小二乘，这样就能追踪到整个图像里所有点的位置（所以这种方式可以拿来做稠密重建，特征点法的话只有特征点被追踪到了，所以只能求出特征点的深度来，这样只能半稠密或者是稀疏重建）

在代码里，看到有calcOpticalFlowPyrLk这个轮子，具体怎么用以后补充。

---

光流法追踪完特征点，相当于只是匹配上了，匹配上以后，计算位姿实际就是上一讲中的那些对极几何或者PnP之类的套路，这样才能算出R和t来。

而直接法是构建了一个光度误差，类似于上一讲的重投影误差，根据误差来优化，进行李代数扰动，直接就算出R和t了。

对于重投影误差来说：是把一个世界坐标系的点，乘了外参，除了第三维，乘了内参，最后变到像素坐标系下，得到一个预测的像素点；把实际的像素点和预测的像素点相减，平方和开根号，就构成一个误差函数。这个误差函数的自变量就是外参，通过调整外参，使得误差最小。（这点和神经网络的损失函数有着本质的区别，因为对于神经网络来说，y=f(x)优化的是f，而这里相当于是不断调整输入的值）

光度误差十分接近重投影误差，它也是想估计一个外参，这样一个像素点A通过这个外参变换到另一张图片的某个位置以后，得到一个预测的点B，用A点的灰度减去这个预测的B点的灰度值，根据灰度不变假设，应该是0，因此构造这么一个优化函数。

从原理上这么一说，是很浅显易懂的。实际这里最后求导得到的两个雅克比矩阵和上一章重投影误差的雅克比矩阵是一样的，因此我想比较分析一下，到底是怎么算出来的，为什么一样。

先说重投影误差：

对于优化这个目标函数，用的是李代数扰动（因为不方便直接对位姿求导为0），所以是对扰动的小量求导，也就是：

关键是这个第三项，高博书里是拆成了两个，第二个很显然，李代数那节已经推过了，第一个他给的雅克比矩阵长这样：

P’是P点经过外参变换到相机坐标系下的点。u是像素坐标下的点，也就是s*u=K*P’

这点很容易被忽视，我有一个问题想问大家，这明明是想求误差对于P’点求导，这为什么拆开是像素点u对于P‘点求导？

之前写上一章的时候我把它忽视了，现在补充到这里：

s*u=K*P’，这个可以代入到重投影误差里，重投影误差就变成了：e=||ui-u||22

这个ui是像素坐标的实际值，u是像素坐标的预测值，实际值不能改变，因此就是一个常量。所以重投影误差e对于P'求导，实际上也就是-u对于P’求导（平方和开根号约掉了）。最后求出来的就是上面的那个结果，还得带个负号了，因为预测值u在后面，如果在前面的话就应该去掉负号。为了对照，列出u和P'的关系来:

其实就是P'除以了第三维Z，然后乘以内参得到的结果嘛，对它求偏导很容易就是上面的雅克比矩阵。而位置关于扰动小量的李代数求导已经在李群李代数那节讲了：[I,-(P')^],也就是：

[ 1, 0, 0, 0, Z, -Y ]

[ 0, 1, 0, -Z, 0, X ]

[ 0, 0, 1, Y, -X, 0 ]

[ 0, 0, 0, 0, 0, 1 ]

上面这是P'关于扰动小量的导数，只取前三维，再由误差关于P'的导数左乘，2*3的矩阵乘以3*6的矩阵，得到一个2*6的矩阵，也就是误差关于扰动小量的导数：

此外，重投影误差也可以求解关于场景坐标P的导数，这个比较简单，等于先对相机坐标系下P'求导，再右乘R。因为P'=RP+t。

再比较光度误差：

这是扰动以后的光度误差，要它对于扰动的小量求偏导。做法就是把扰动量泰勒展开，保留一阶项，最后就得到：

这时候，提出两个量：

第一个量是q，代表扰动的小量在第二个相机坐标系下的坐标：

再把扰动的小量从相机坐标系下的坐标p变换到像素坐标系下，得到第二个量u：

这样做的目的是想把小量给提出来，好单独求导：

搞一波泰勒展开，先回顾一下泰勒展开啊，这里的泰勒展开是f（x+△x）的泰勒展开（书111页）：

对I2（）展开，I1不变，I2中u看成是小量，泰勒展开后，一堆偏导数当成J（x），小量δξ当成是△x：

 

J（x）中的第一项，I2对于u的偏导数，就是u处（扰动的小量的像素坐标）的像素梯度；

第二项，u关于q的偏导数，注意q是扰动小量的相机坐标系下的坐标，u是扰动小量的预测的像素坐标系下的坐标，在重投影误差中，第一个雅克比矩阵是求的预测像素点坐标对于相机坐标系下坐标的偏导，而在光度误差这里是求的扰动小量的预测的像素坐标系下坐标对于相机坐标系下坐标的偏导，本质上都是像素坐标对相机坐标求偏导，因此雅克比矩阵的形式是一样的：

第二项是三维点对于小量位姿的导数，还是李代数那章的内容，76页，我的笔记在SLAM14讲学习笔记（一) 李群李代数基础

最后合在一起：

这个长得和重投影误差对于扰动小量求偏导的雅克比矩阵是很相近的：

不过对于重投影误差对于扰动小量求偏导的结果来说，上面的2*6的雅克比矩阵就是最后的值了。
可是对于光度误差来说，还没完呢：

这才是最后的结果。

得到雅克比矩阵以后，这就和非线性优化那节的内容串起来了，再复习一下：一阶和二阶梯度法，一个是太贪心了，一个是得计算海塞矩阵H；高斯牛顿法用雅克比矩阵与自身转置的乘积作为海塞矩阵H的近似，列文伯格马尔夸特方法也是差不多的做法，这样求解增量△x，也就是扰动的小量，然后用原先的位姿加上这个小量，作为新的位姿，下一轮迭代，进而找到最优解。

学到这里我才感觉，真正前后的内容融会贯通起来了。非线性优化基础的内容：

SLAM14讲学习笔记（三）非线性优化基础

之前学的时候，不明白那个基础有什么用，现在发现这就是它真正的用途。这个误差也就可以放到那节的观测方程和状态方程套进去的联合优化函数之内了。

---

到这里，大头就总结完了，感觉总结确实有点用处，因为很多东西都是自己在写总结的时候领悟到的，光看书容易造成一个错觉就是自己会了，在总结并且给别人讲的的时候，才能发现自己之前没有发现的问题。第一次通读SLAM14讲的时候，到后面就看不懂代码了，一个原因是当时赶着在写项目书之前掌握SLAM的基础，太着急了，另一个原因就是对理论了解不够深刻！理论都看不懂，写成代码更觉得是天书了。

最后几点讨论：

1.在上面的介绍中，P是已知的，深度是知道的。对于RGBD相机，确实是直接能知道，但是对于别的需要深度估计。高博说13讲会讲，回头我把笔记链接放上来。（参见这里：SLAM14讲学习笔记（九）单目稠密重建、深度滤波器详解与补充（纠正第13讲 建图 中的错误））

2.对于光度误差的雅克比矩阵J，第一项是灰度对于扰动小量像素坐标的导数，也就是梯度，如果梯度是0，也就是说扰动完以后，灰度没变，那雅克比矩阵就是0，之后构成的海塞矩阵H也是0，求不出扰动小量△x了。所以可以考虑只用带有梯度的像素点。

3.直接法的优点：不用算描述子，不用特征点匹配，检测完直接追踪就完事了；或者都不用检测，直接用有像素梯度的地方追踪就行（只有渐变的图像，特征点法不能提角点，但是这个就能追踪）；可以稠密重建；

缺陷：完全依靠梯度搜索，因此运动很小才能成功；另外单个像素没有区分度，用所有的像素一起估计的话，说白了就是少数服从多数；另外灰度不变性也容易导致优化失败。