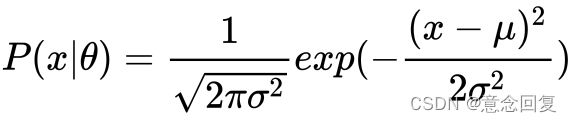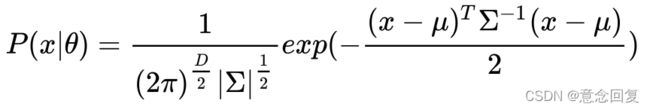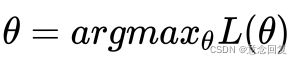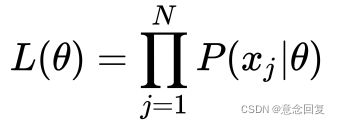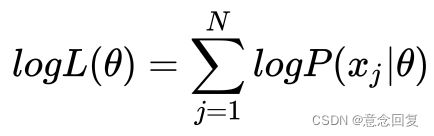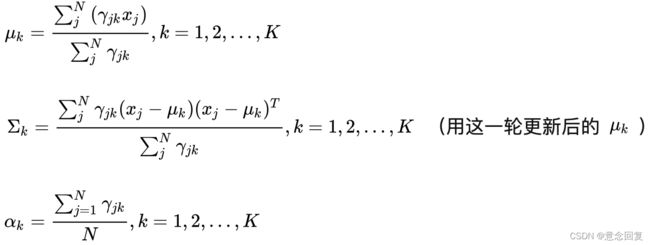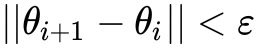机器学习算法(二十九):高斯混合模型(Gaussian Mixed Model,GMM)
目录
1 混合模型(Mixture Model)
2 高斯模型
2.1 单高斯模型
2.2 高斯混合模型
3 模型参数学习
3.1 单高斯模型
3.2 高斯混合模型
4 高斯混合模型与K均值算法对比
1 混合模型(Mixture Model)
混合模型是一个可以用来表示在总体分布(distribution)中含有 K 个子分布的概率模型,换句话说,混合模型表示了观测数据在总体中的概率分布,它是一个由 K 个子分布组成的混合分布。混合模型不要求观测数据提供关于子分布的信息,来计算观测数据在总体分布中的概率。
2 高斯模型
2.1 单高斯模型
当样本数据 X 是一维数据(Univariate)时,高斯分布遵从下方概率密度函数(Probability Density Function):
其中 ![]() 为数据均值(期望),
为数据均值(期望), ![]() 为数据标准差(Standard deviation)。
为数据标准差(Standard deviation)。
当样本数据 X 是多维数据(Multivariate)时,高斯分布遵从下方概率密度函数:
其中, ![]() 为数据均值(期望),
为数据均值(期望),![]() 为协方差(Covariance),D 为数据维度。
为协方差(Covariance),D 为数据维度。
2.2 高斯混合模型
高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型,这 K 个子模型是混合模型的隐变量(Hidden variable)。一般来说,一个混合模型可以使用任何概率分布,这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能。
说起高斯分布,大家都不陌生,通常身高、分数等都大致符合高斯分布。因此,当我们研究各类数据时,假设同一类的数据符合高斯分布,也是很简单自然的假设;当数据事实上有多个类,或者我们希望将数据划分为一些簇时,可以假设不同簇中的样本各自服从不同的高斯分布,由此得到的聚类算法称为高斯混合模型。
高斯混合模型的核心思想是,假设数据可以看作从多个高斯分布中生成出来的。在该假设下,每个单独的分模型都是标准高斯模型,其均值![]() 和方差
和方差![]() 是待估计的参数。此外,每个分模型都还有一个参数
是待估计的参数。此外,每个分模型都还有一个参数![]() ,可以理解为权重或生成数据的概率。高斯混合模型的公式为
,可以理解为权重或生成数据的概率。高斯混合模型的公式为
高斯混合模型是一个生成式模型。可以这样理解数据的生成过程,假设一个最简单的情况,即只有两个一维标准高斯分布的分模型N(0,1)和N(5,1),其权重分别为0.7和0.3。那么,在生成第一个数据点时,先按照权重的比例,随机选择一个分布,比如选择第一个高斯分布,接着从N(0,1)中生成一个点,如−0.5,便是第一个数据点。在生成第二个数据点时,随机选择到第二个高斯分布N(5,1),生成了第二个点4.7。如此循环执行,便生成出了所有的数据点。
3 模型参数学习
3.1 单高斯模型
对于单高斯模型,我们可以用最大似然法(Maximum likelihood)估算参数 ![]() 的值,
的值,
这里我们假设了每个数据点都是独立的(Independent),似然函数由概率密度函数(PDF)给出。
由于每个点发生的概率都很小,乘积会变得极其小,不利于计算和观察,因此通常我们用 Maximum Log-Likelihood 来计算(因为 Log 函数具备单调性,不会改变极值的位置,同时在 0-1 之间输入值很小的变化可以引起输出值相对较大的变动):
3.2 高斯混合模型
对于高斯混合模型,Log-Likelihood 函数是:
如何计算高斯混合模型的参数呢?这里我们无法像单高斯模型那样使用最大似然法来求导求得使 likelihood 最大的参数,因为对于每个观测数据点来说,事先并不知道它是属于哪个子分布的(hidden variable),因此 log 里面还有求和,对于每个子模型都有未知的 ![]() ,直接求导无法计算。需要通过迭代的方法求解。
,直接求导无法计算。需要通过迭代的方法求解。
通常我们并不能直接得到高斯混合模型的参数,而是观察到了一系列数据点,给出一个类别的数量K后,希望求得最佳的K个高斯分模型。因此,高斯混合模型的计算,便成了最佳的均值μ,方差Σ、权重π的寻找,这类问题通常通过最大似然估计来求解。遗憾的是,此问题中直接使用最大似然估计,得到的是一个复杂的非凸函数,目标函数是和的对数,难以展开和对其求偏导。
在这种情况下,可以用上一节已经介绍过的EM算法框架来求解该优化问题。
EM算法是在最大化目标函数时,先固定一个变量使整体函数变为凸优化函数,求导得到最值,然后利用最优参数更新被固定的变量,进入下一个循环。具体到高斯混合模型的求解,EM算法的迭代过程如下。
首先,初始随机选择各参数的值。然后,重复下述两步,直到收敛。
(1)E步骤。根据当前的参数,计算每个点由某个分模型生成的概率。
(2)M步骤。使用E步骤估计出的概率,来改进每个分模型的均值,方差和权重。
也就是说,我们并不知道最佳的K个高斯分布的各自3个参数,也不知道每个数据点究竟是哪个高斯分布生成的。所以每次循环时,先固定当前的高斯分布不变,获得每个数据点由各个高斯分布生成的概率。然后固定该生成概率不变,根据数据点和生成概率,获得一个组更佳的高斯分布。循环往复,直到参数的不再变化,或者变化非常小时,便得到了比较合理的一组高斯分布。
通过 EM 迭代更新高斯混合模型参数的方法(我们有样本数据 ![]() 和一个有
和一个有 ![]() 个子模型的高斯混合模型,想要推算出这个高斯混合模型的最佳参数):
个子模型的高斯混合模型,想要推算出这个高斯混合模型的最佳参数):
- M-step:计算新一轮迭代的模型参数
至此,我们就找到了高斯混合模型的参数。需要注意的是,EM 算法具备收敛性,但并不保证找到全局最大值,有可能找到局部最大值。解决方法是初始化几次不同的参数进行迭代,取结果最好的那次。
4 高斯混合模型与K均值算法对比
高斯混合模型与K均值算法的相同点是:
- 它们都是可用于聚类的算法;
- 都需要指定K值;
- 都是使用EM算法来求解;
- 都往往只能收敛于局部最优。
而它相比于K均值算法的优点是:
- 可以给出一个样本属于某类的概率是多少;
- 不仅仅可以用于聚类,还可以用于概率密度的估计;
- 并且可以用于生成新的样本点。
高斯混合模型(GMM) - 知乎