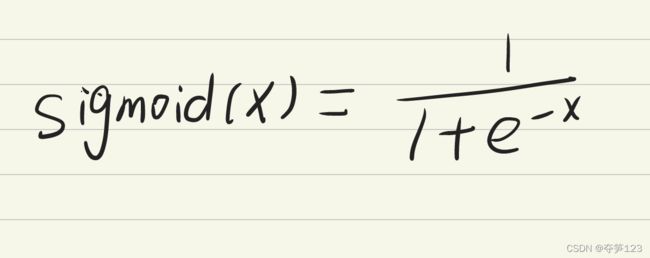从零到一实现神经网络（python）:二

问题引入

上一节我们介绍了感知机，实际上，通过叠加感知机层数我们能够解决很多复杂的问题
但是上一节我们通过感知机实现简单逻辑电路的例子中，缺点依然明显，输入权重都是人为设定的
神经网络的出现完美的解决了这个问题，它可以自动从数据中学习到合适的权重参数

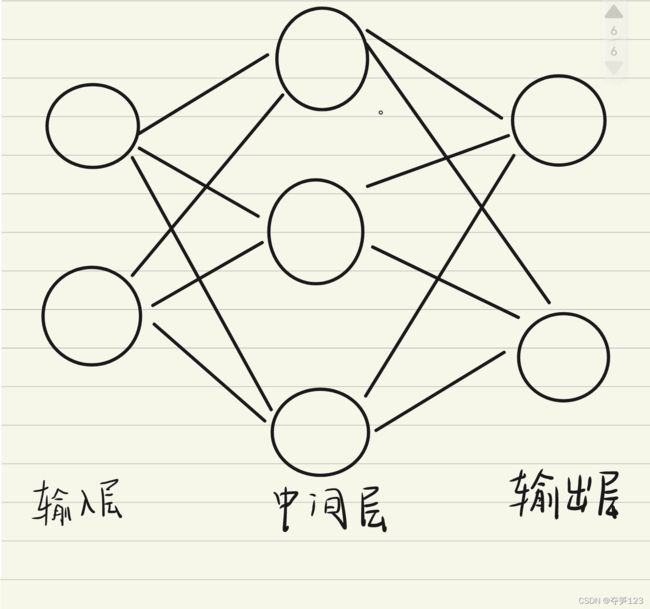
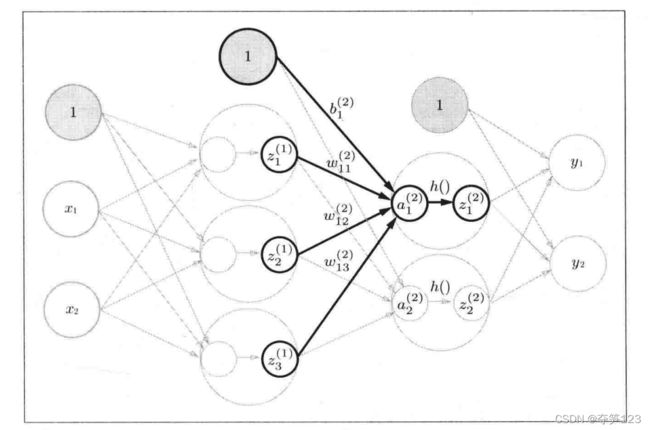
神经网络的例子

我们下面举出一个具有三层神经元的网络

感知机中的信号传递机制

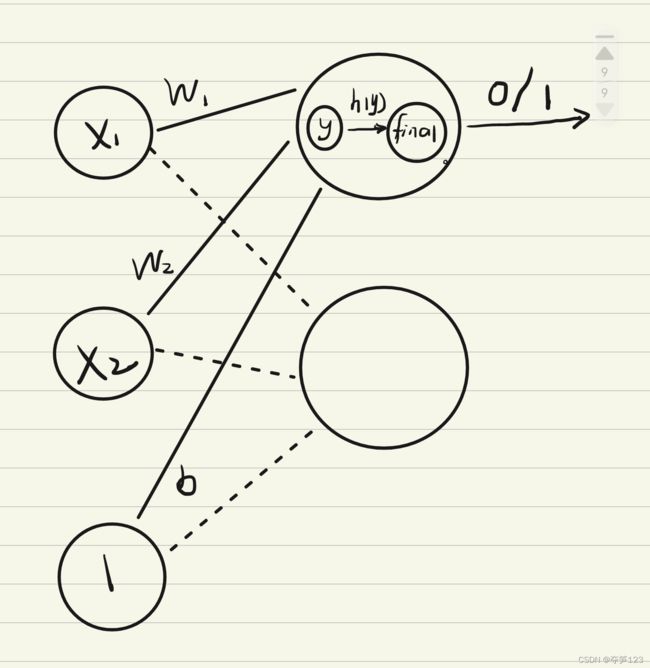
单层感知机中输出层与输入层之间的函数关系

在上一节中，感知机通过将输入信号加权求和得到拟输出，拟输出大于阈值时输出1，否则输出0
用数学表达式表示为

仔细观察我们会发现实际上最终final与输入变量x之间并非单一的函数关系，即：

1. 拟输出y与x有一层函数关系，
2. 最终输出final与拟输出y有另外一层函数关系

信号传递过程图解

阶跃函数

在感知机算法中，我们将上面的未知函数定义为阶跃函数，它的作用是将输入信号的加权和（即拟输出y）转换为最终输出值（即final），它的函数图像为

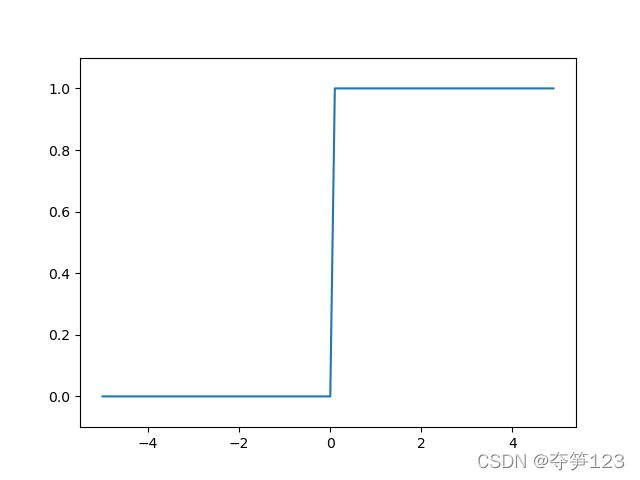
阶跃函数实现

def step_funtion(x):
	return 1 if x>0 else 0

def step_fun(x):
	'''x:ndarray'''
	y=x>0
	return y.astype(np.int)
	
def step_fun(x):
	'''x:ndarray'''
	return np.array(x>0,dtype=np.int)	

神经网络中的信号传递机制

神经网络中的符号

现在用带有2个隐藏层的4层神经网络举例

利用线性代数对数学而表达式进行优化

我们再来回顾一下输入层与隐藏层之间的网络表示

关于偏置b：我们会发现这张图片与上面的图片不太一样——似乎在输入层多了一个神经元，其实笔者只是在上一个图中省略了，带有偏置神经元的神经网络层（包括输入层和隐藏层）才是正确。
上一节的感知机中我们知道了偏置值b的由来：它表示的神经元的阈值，反映了一个神经元被激活的容易程度，因此每个神经元在接受输入值时都应该加上偏置值

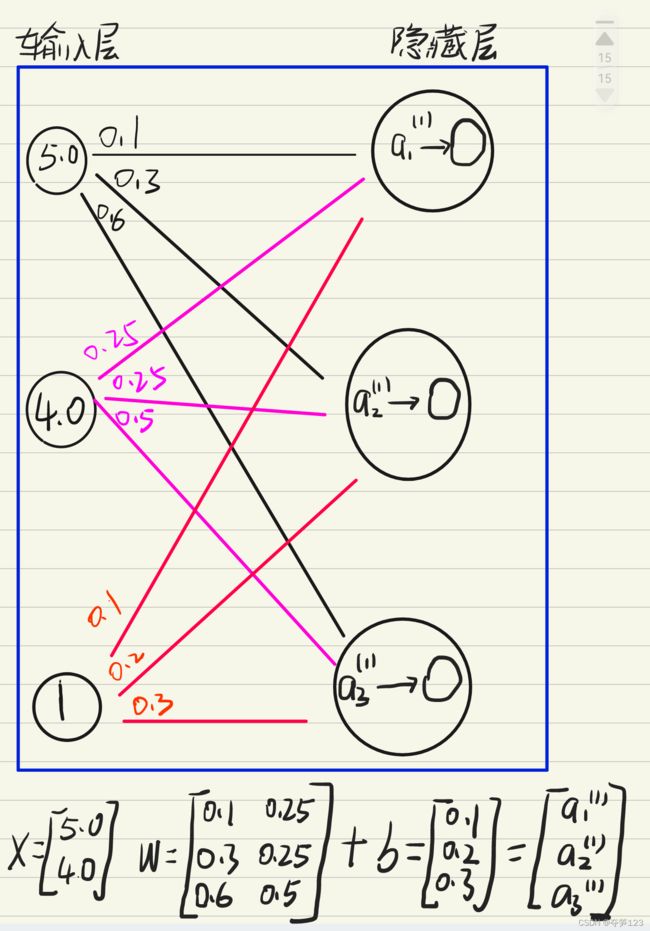
现在我们已经知道了，上面神经网络中隐藏层1中第一个神经元a1的值如下

如果输入层的神经元数量较多，上面的式子将会变得十分冗长，因此我们可以将输入值x和权重w都使用矩阵表示

如果将隐藏层1的所有神经元都是用一个代数式表示，则

知道了数学原理，我们如何在代码中实现矩阵相乘？

numpy的广播机制

广播是一个术语，它描述的是 numpy 如何在算术运算期间处理具有不同形状的数组。它是一个广义概念，我们在这里只使用到其中的np.dot()函数计算输入值与权重参数的内积

我们举例说明，假设输入值与权重参数如下所示

代码实现

import numpy as np
X=np.array([5.0,4.0])
W1=np.array([[0.1,0.3,0.6],[0.25,0.25,0.5]])
B1=np.array([0.1,0.2,0.3])
A1=np.dot(X,W1)+B1
print(A1)
# [1.6 2.7 5.3]

激活函数登场

在单层感知机中得到的拟输出与最终输出之间存在一层函数关系，称为阶跃函数，它表示神经元接受的输入值达到一定阈值时才会被激活产生输出。神经网络与之类似，我们上面得到的矩阵A1实际上就是隐藏层1的拟输出矩阵，要想得到隐藏层1的最终输出，我们也需要在两者之间架设一层函数关系，
然而我们看到阶跃函数的图像过于突兀，在函数值在拟输出值大于0后骤然上升，这让它看起来冷冰冰的，不太符合实际，因此经过学者的研究，在神经网络中使用其他的函数来代替，其中比较著名的是sigmoid函数

激活函数能否为线性函数？
不能，线性函数的使用会使神经网络的层数加深没有意义。线性函数通常指输入值为输出值的常数倍的函数，如h(x)=cx+b（c、b为常数）。如果使用线性函数作为激活函数，对于一个三层神经网络y(x)=h(h(h(x)))，即y=ccc*x+…它等价于单层神经网络y=pow(c,3)*x+…

sigmoid函数

函数关系数学表达式

函数图像

从图像上来看，sigmoid函数比较平滑，这意味着输出值会随着输入值发生连续性的变化，这一点对于神经网络的学习过程（权重更新）有着至关重要的意义

代码实现

def sigmoid(x):
	return 1/(1+np.exp(-x))

神经网络中各层之间的信号传递

我们依旧使用那个带有2个隐藏层的4层神经网络作为例子

输入层到隐藏层1

隐藏层1到隐藏层2

隐藏层2到输出层

代码实现

前三层的信号传递极为相似，在此一并使用代码实现

def init_network():
    network={}
    # 下面参数为随意设置的值，注意数据维度
    network['W1']=np.array([[0.2,0.4,0.4],[0.1,0.3,0.6]])
    network['B1']=np.array([0.1,0.3,0.2])
    network['W2']=np.array([[0.1,0.1],[0.3,0.4],[0.3,0.6]])
    network['B2']=np.array([0.4,0.3])
    network['W3']=np.array([[0.1,0.3],[0.2,0.4]])
    network['B3']=np.array([0.1,0.2])

    return network

def forward(network,x):
	# 确定权重参数以及偏置
    W1,W2,W3=network['W1'],network['W2'],network['W3']
    B1,B2,B3=network['B1'],network['B2'],network['B3']
	# 计算各层拟输出及最终输出
    A1=np.dot(x,W1)+B1
    z1=sigmoid(A1)
    A2 = np.dot(z1, W2) + B2
    z2 = sigmoid(A2)
    A3 = np.dot(z2, W3) + B3
    y = sigmoid(A3)

    return y


my_network=init_network()
x=np.array([5.0,4.0])
y=forward(my_network,x)
print(y)
# [0.58266985 0.67742112]

通过上面代码我们已经能够通过输入值矩阵计算得到输出层的拟输出矩阵了！下面我们看看输出层的最终输出值怎么计算

经过上面的代码，我们已经基本将神经网络的前向信号传播操作了一遍，看似神秘的神经网络就这么被我们实现了一半！

输出层的输出

机器学习可以大致分为回归问题和分类问题，前者要做的是将数据正确分类，后者则是要根据一个输入值预测一个连续性数值
对于神经网络的输出层一般回归问题用恒等函数，分类问题一般用softmax函数

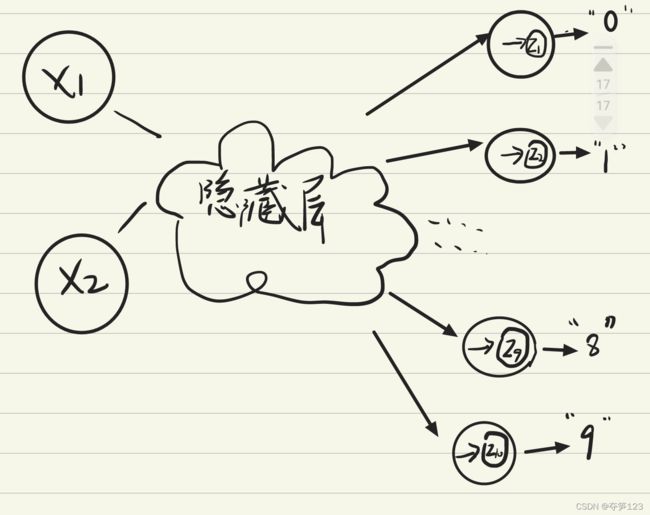
输出层的神经元设置

需要根据具体的问题进行设置，比如现在给定一张28x28的mnist手写数据集图片，对其分类，就需要将输出层神经元数量设置为10

恒等函数

接收输入x，输出x

def identical(x):
	return x

softmax函数

数学表达式

分类问题使用softmax函数的数学原理

在上面的图片中，需要对一张图片分类，共十个类别。输入值在经过隐藏层计算后，得到输出层的拟输出矩阵A1=[a1,a2,…,a10]，这个矩阵已经可以表达出整个神经网络的最终输出（通常取矩阵中相对值最大的元素对应的标签作为最终预测标签）

但是这个矩阵中的元素不一定都是正值，为了方便比较相对值，我们使用一个单调递增函数（此处选取底数为e的指数函数），同时，我们采取比例形式比较出最终的相对值

于是softmax函数的形式便出现了

这样我们得到了输出层的最终输出值矩阵Z=[z1,z2,…]，其中所有元素和为1，每个元素代表属于对应标签的概率

softmax函数代码实现

def softmax(x):
	return(np.exp(x)/np.sum(np.exp(x)))

softmax函数应用于计算机时的缺陷

指数函数具有一个“指数爆炸”的特性，即函数值随自变量x的值增加会增加的十分迅速，如pow(e,40)的值为一个后面有40多个零的超大数值，这会造成计算机的溢出问题
为解决这一问题，可以从softmax函数的性质出发

上述性质表明，加上或减去某个常数值不会导致sofmax函数值发生改变，为防止溢出我们通常使用数组x中的最大值，下面对softmax函数的代码实现进行改进

def softmax(x):
	c=np.max(x)
	return np.exp(x-c)/np.sum(np.exp(x-c))

关于softmax函数的其他

由于指数函数的单调递增性，因此拟输出值最大的神经元位置不会发生改变，softmax只起到了计算比例的作用（神经网络的最终输出信息保存在拟输出矩阵A中，但是人类一般不能够太直观的根据其中蕴含的信息推断出最终输出，因此从这个角度来说，softmax有一定作用
softmax函数的另一个作用是神经网络的权重更新过程的误差传递（见下一节）