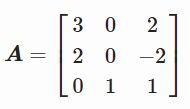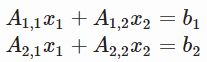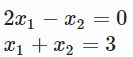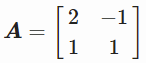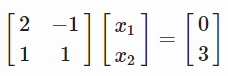机器学习笔记 - 单位矩阵和逆矩阵

        这里学习在线性代数中很重要的单位矩阵和逆矩阵。

一、单位矩阵

1、单位矩阵

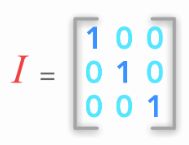
        单位矩阵是一个形状为 (n×n) 的除了对角线为1，其余均为0的矩阵。

一个 3 x 3 单位矩阵

        可以使用 Numpy函数eye()创建单位矩阵：

np.eye(3)

打印输出如下

[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

2、运算示例

        单位矩阵乘以向量，结果为原向量。

        python代码如下

x = np.array([[2], [6], [3]])
xid = np.eye(x.shape[0]).dot(x)
print(xid)

        打印结果如下

[[2.]
 [6.]
 [3.]]

二、逆矩阵

        设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=（单位矩阵） ，则称方阵A可逆，并称方阵B是A的逆矩阵。

         python求逆矩阵

A = np.array([[3, 0, 2], [2, 0, -2], [0, 1, 1]])
A_inv = np.linalg.inv(A)
print(A_inv)

        结果打印如下

[[ 0.2  0.2  0. ]
 [-0.2  0.3  1. ]
 [ 0.2 -0.3 -0. ]]

        如何检查是否是逆矩阵,使用原矩阵乘逆矩阵，就是求点积，但是精度会损失

A_bis = A_inv.dot(A)
print(A_bis)

         结果打印如下

[[ 1.00000000e+00  0.00000000e+00 -1.11022302e-16]
 [ 0.00000000e+00  1.00000000e+00  0.00000000e+00]
 [ 0.00000000e+00  0.00000000e+00  1.00000000e+00]]

         如果自行计算，这两个矩阵的点积

         如下计算

[3*0.2 + 0*-0.2 + 2*0.2 = 1,  3*0.2 + 0*0.3 + 2*-0.3 = 0,  3*0 + 0*1 + 2*-0 = 0]
[2*0.2 + 0*-0.2 + -2*0.2 = 0,  2*0.2 + 0*0.3 + -2*-0.3 = 1,  2*0 + 0*1 + -2*-0 = 0]
[0*0.2 + 1*-0.2 + 1*0.2 = 0,  0*0.2 + 1*0.3 + 1*-0.3 = 0,  0*0 + 1*1 + 1*-0 = 1]

         即得到单位矩阵

[[ 1  0  0 ]
 [ 0  1  0 ]
 [ 0  0  1 ]]

三、求解线性方程组

        有下面这样两个方程

y=2x
y=−x+3

        我们转换为如下的形式

       ，即

         我们将得到权重矩阵

         以及各个方程解的向量 b 为

        所以矩阵形式下的方程变为

         让我们使用python来进行求解。

# 权重矩阵求逆
A = np.array([[2, -1], [1, 1]])
A_inv = np.linalg.inv(A)
b = np.array([[0], [3]])
# 求点积
x = A_inv.dot(b)
print(x)

         打印结果如下

[[1.]
 [2.]]

         这就是说坐标点 (1, 2) 是解，位于表示方程的线的交点处。让我们使用plt库进行可视化：

import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-10, 10)
y = 2*x
y1 = -x + 3

#plt.figure()
plt.plot(x, y)
plt.plot(x, y1)
plt.xlim(0, 3)
plt.ylim(0, 3)
# draw axes
plt.axvline(x=0, color='grey')
plt.axhline(y=0, color='grey')
plt.show()
plt.close()

可以看到交点位于（1，2）