【2018年蓝桥杯Java-B组省赛题解】
2018Java-B组省赛
-
-
- 一、第几天(Calendar类)
- 二、方格计数(模拟)
- 三、复数幂(模拟)
- 四、测试次数(动态规划、鸡蛋掉落问题)
- 五、程序填空题
- 六、递增三元组(模拟、双指针)
- 七、螺旋折线(模拟、找规律)
- 八、日志统计(排序、滑动窗口)
- 九、全球变暖(DFS搜索)
- 十、堆的计数
-
一、第几天(Calendar类)
2000年的1月1日,是那一年的第1天。
那么,2000年的5月4日,是那一年的第几天?
直接用Calendar类,注意月份从0开始。
package Chapter_5;
import java.util.*;
public class Main {
public static void main(String[] args) {
Calendar cal = Calendar.getInstance();
cal.set(2000, 4, 4);
System.out.println(cal.get(Calendar.DAY_OF_YEAR));
}
}
答案:125
二、方格计数(模拟)

根据圆的对称性,只用考虑1/4个圆即可,遍历1/4圆内的所有方块的右上角顶点,看它与圆心的距离,小于等于半径,计数++,最后结果 * 4。
package Chapter_5;
import java.util.*;
public class Main {
public static void main(String[] args) {
int ans = 0;
for (int i = 1; i <= 1000; i++) {
for (int j = 1; j <= 1000; j++) {
if (i * i + j * j <= 1000000) ans++;
}
}
System.out.println(ans * 4);
}
}
答案:3137548
三、复数幂(模拟)
设i为虚数单位。对于任意正整数n,(2+3i)^n 的实部和虚部都是整数。
求 (2+3i)^123456 等于多少? 即(2+3i)的123456次幂,这个数字很大,要求精确表示。
答案写成 "实部±虚部i" 的形式,实部和虚部都是整数(不能用科学计数法表示),中间任何地方都不加空格,实部为正时前面不加正号。(2+3i)^2 写成: -5+12i,
(2+3i)^5 的写成: 122-597i
package Chapter_5;
import java.math.BigInteger;
import java.util.*;
public class Main {
public static void main(String[] args) {
// (a + bi) * (c + di) = ac + (ad + bc) * i + (-1)bd
// = ac - bd + (ad + bc) * i
// 把实部和虚部分开统计即可
// 2 + 3i
BigInteger x = BigInteger.valueOf(2);
BigInteger y = BigInteger.valueOf(3);
for (int i = 2; i <= 123456; i++) {
// ac
BigInteger a = x.multiply(BigInteger.valueOf(2));
// bd
BigInteger b = y.multiply(BigInteger.valueOf(3));
// ad
BigInteger c = x.multiply(BigInteger.valueOf(3));
// bc
BigInteger d = y.multiply(BigInteger.valueOf(2));
x = a.subtract(b);
y = c.add(d);
}
String ans = "";
if (y.compareTo(BigInteger.valueOf(0)) < 0) {
ans = x + "" + y + "i";
} else {
ans = x + "+" + y + "i";
}
System.out.println(ans);
}
}
答案:
太长写博客爆内存了!
这道题答案太长了,再出这样题目的可能性很小,但要知道模拟多项式幂运算的方法。
四、测试次数(动态规划、鸡蛋掉落问题)
x星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通。
x星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的2楼。
如果手机从第7层扔下去没摔坏,但第8层摔坏了,则手机耐摔指数=7。
特别地,如果手机从第1层扔下去就坏了,则耐摔指数=0。
如果到了塔的最高层第n层扔没摔坏,则耐摔指数=n
为了减少测试次数,从每个厂家抽样3部手机参加测试。
某次测试的塔高为1000层,如果我们总是采用最佳策略,在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?
请填写这个最多测试次数。
这道题和LeetCode的鸡蛋掉落是一类题型,把下面的题搞懂了,上面的题自然也会做了。
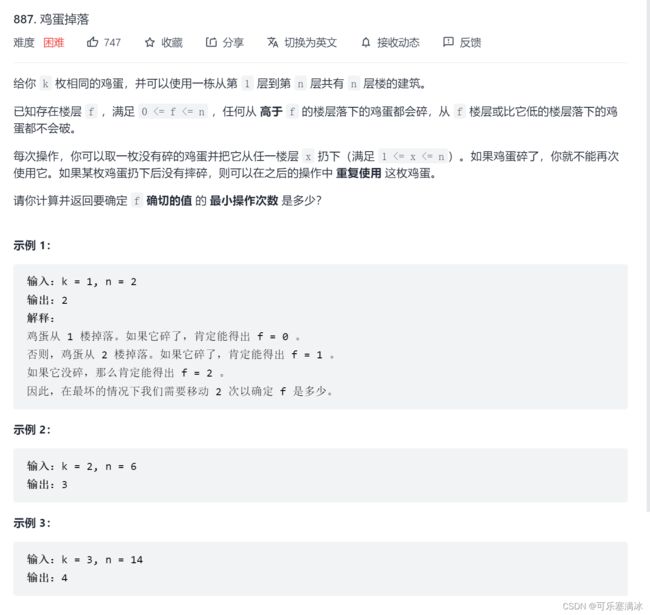
先从1个鸡蛋摔起,假设有6层楼1-6,从第一层开始摔,摔到哪一层碎了,就可以确定f = 该层数 - 1,试验的次数 = 该层数(注意,这里必须从第一层开始摔,不能从最高层)。
注意!!这些都是建立在:最坏的情况下找最小操作次数,最坏的情况就是不考虑运气成分,例如有6层楼,1个鸡蛋,最坏情况就是第6层楼才碎,那至少就需要6次操作。如果不考虑最坏情况,那可能六层楼,第一层楼就摔碎了,那不就只需要1次。(当然,如果鸡蛋数量不限制,那么用二分就可以求得最小操作次数,由于鸡蛋数量可以变,才导致了无法使用二分)
对于n个鸡蛋,现在只有1层楼,那无论几个鸡蛋,都只需要1次(如果碎了,f = 0,没碎,f = 1)。
对于n个鸡蛋,现在没有一层楼,没有机会扔,那么一次也不能够。‘
对于0个鸡蛋,n层楼,没有机会扔,那么一次也不能够。
drop(totalEggs, totalFloors),记录n个鸡蛋,(剩下)n个楼层,在最坏情况下,所需的最小操作次数。
// 楼层的特殊情况
if (totalFloors == 1 || totalFloors == 0) return totalFloors;
// 鸡蛋的特殊情况
if (totalEggs == 1) return totalFloors;
现在有3个鸡蛋,6层楼,drop(3,6) 可以拆分成:drop(3,1) drop(3,2) drop(3,3) drop(3,4) drop(3,5) drop(3,6),六种策略(注意,这六种策略并不包含运气成分,本身就存在这六种策略,我们只需要找到这六种策略里面的最小值即可),代表着从1、2、3、4、5、6楼扔。每一种又有两种情况:摔碎、没摔碎。drop(3,6),如果没碎,那么就应该考虑更高层:第7层,但是这里我们只考虑六层楼,那就是说已经把六层楼遍历完了,那还剩下0层楼要扔,那就 = drop(3,0),同理,对于第五层楼,如果鸡蛋还没碎,应该迁移到drop(3,1),因为还剩下1层楼要扔。
如果drop(3,6),鸡蛋碎了,那么鸡蛋数要-1,必须往更低楼层考虑,迁移到drop(2,5)。
按照上面的分析可以画出这个动态规划表:

把可以直接推得的信息填入后,如何确定drop(2,2)?
drop(2,2)的策略可以分为:drop(2,1)、drop(2,2),就是说可以把两个鸡蛋从1楼扔、从2楼扔,我们需要的是最小操作次数,那么应该是求最小的情况。前面已经提到了,分策略并不存在运气成分。 drop(2,1)、drop(2,2)又分为两种情况:鸡蛋碎与没碎,碎了的话就是drop(1, 0)、drop(1,1);没碎的话就是drop(2, 1)、drop(2, 0)。
再次强调一下:什么叫做最坏情况下?
对于2个鸡蛋,2层楼,我们可以从第一层楼开始扔,或者第二层楼开始扔,不管从哪层楼开始扔,鸡蛋都不是在最开始一丢下就碎了,例如:从第一层楼开始扔,并不是第一层楼扔下就碎了,而是要在最后扔到第二层楼还没碎,这才是最坏情况!从第二层楼扔,最坏的情况就是一扔就碎,但是不知道是1还是2,所以还要扔一次。
碎和没碎,该如何选择呢?
我们应该选择最大值的情况,来保证是“最坏情况”(因为更大值,代表更多的操作次数,意味着越不包含运气成分,是最坏情况),假设我们按最小值来取,drop(2,1)的策略 = 0 + 1(因为到达drop(1,0)或者drop(1,1)又需要丢一次鸡蛋),而drop(2,2)的策略 = 0 + 1,那么整体看,drop(2,2) = 1,想想看,2个鸡蛋,2层楼,最坏情况,怎么也得丢2次。
所以可以得到状态转移方程:
d p [ i ] [ j ] = m i n ( d p [ i ] [ 1 ] , d p [ i ] [ 2 ] . . . d p [ i ] [ j ] ) + 1 其 中 , d p [ i ] [ 1 ] = m a x ( d p [ i − 1 ] [ 1 − 1 ] , d p [ i ] [ j − 1 ] ) d p [ i ] [ 2 ] = m a x ( d p [ i − 1 ] [ 2 − 1 ] , d p [ i ] [ j − 2 ] ) . . . d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j − 1 ] , d p [ i ] [ j − j ] ) dp[i][j] = min(dp[i][1], dp[i][2]...dp[i][j]) + 1\\ 其中,dp[i][1] = max(dp[i - 1][1 - 1], dp[i][j - 1])\\ dp[i][2] = max(dp[i - 1][2 - 1], dp[i][j - 2])\\ ...\\ dp[i][j] = max(dp[i-1][j-1],dp[i][j-j]) dp[i][j]=min(dp[i][1],dp[i][2]...dp[i][j])+1其中,dp[i][1]=max(dp[i−1][1−1],dp[i][j−1])dp[i][2]=max(dp[i−1][2−1],dp[i][j−2])...dp[i][j]=max(dp[i−1][j−1],dp[i][j−j])

有了上面分析可以写出最直白的代码(超时,但是思路是对的)
class Solution {
public int superEggDrop(int k, int n) {
// dp[i][j]: i个鸡蛋,j层楼,在最坏情况下,所需最小操作数
int[][] dp = new int[k + 1][n + 1];
for (int i = 1; i <= n; i++) {
// 1个鸡蛋,最坏情况下,至少要尝试 i 层楼
// 必须要确保能够找到 f
dp[1][i] = i;
}
for (int i = 1; i <= k; i++) {
// 1层楼,无论有几枚鸡蛋(>=1),都要 1 次
dp[i][1] = 1;
}
// 鸡蛋
for (int i = 2; i <= k; i++) {
// 楼层
for (int j = 2; j <= n; j++) {
int min = Integer.MAX_VALUE;
// 遍历每种策略
for (int l = 1; l <= j; l++) {
// 内层的max保证最坏情况下,外层的min保证最少的操作数
min = Math.min(min, Math.max(dp[i][j - l], dp[i - 1][l - 1]) + 1);
}
dp[i][j] = min;
}
}
return dp[k][n];
}
}
考虑中间遍历每种策略,实际是在固定鸡蛋数目的情况下,遍历每种楼层找到最大值,这部分可以用二分优化
class Solution {
public int superEggDrop(int k, int n) {
// dp[i][j]: i个鸡蛋,j层楼,在最坏情况下,所需最小操作数
int[][] dp = new int[k + 1][n + 1];
for (int i = 1; i <= n; i++) {
// 1个鸡蛋,最坏情况下,至少要尝试 i 层楼
// 必须要确保能够找到 f
dp[1][i] = i;
}
for (int i = 1; i <= k; i++) {
// 1层楼,无论有几枚鸡蛋(>=1),都要 1 次
dp[i][1] = 1;
}
// 鸡蛋
for (int i = 2; i <= k; i++) {
// 楼层
for (int j = 2; j <= n; j++) {
int min = Integer.MAX_VALUE;
int left = 1;
int right = j;
int mid;
// 遍历每种策略的时候,鸡蛋数是固定的
// 变化的是楼层数,需要找到最大值,可以用二分
while (left <= right) {
mid = left + (right - left) / 2;
int broken = dp[i - 1][mid - 1];
int not_broken = dp[i][j - mid];
// 取两种情况中最坏的情况(就是丢的次数最多的)
if (broken > not_broken) {
// 鸡蛋坏了,那么只用考虑当前楼层下面的楼层
right = mid - 1;
min = Math.min(min, broken + 1);
} else {
// 鸡蛋没坏,那么只用考虑当前楼层更高的楼层
left = mid + 1;
min = Math.min(min, not_broken + 1);
}
}
dp[i][j] = min;
}
}
return dp[k][n];
}
}
但是上面两种方法,时间花费都高,虽然方便理解但是代码冗长,有没有更好办法?
class Solution {
public int superEggDrop(int K, int N) {
// dp[i][j] i 个鸡蛋扔 j 次能确定的层数
int[][] dp = new int[K + 1][N + 1];
// 注意先遍历扔的次数
// 扔j次
for (int j = 1; j <= N; j ++) {
dp[0][j] = 0;
// i个鸡蛋
for (int i = 1; i <= K; i ++) {
// 如果碎了,确定 F 在碎的层数下面,即确定层数区间是 dp[i - 1][j - 1]
// 如果没碎,确定 F 在扔的那一层 或者 扔的层数上面,即 1 + dp[i][j - 1]
dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1] + 1;
// 直到能够确定的最大区间层数 >= N,就可以返回答案
if (dp[i][j] >= N) {
return j;
}
}
}
return N;
}
}
1、无论你在哪层楼扔鸡蛋,鸡蛋只可能摔碎或者没摔碎,碎了的话就测楼下,没碎的话就测楼上。
2、无论你上楼还是下楼,总的楼层数 = 楼上的楼层数 + 楼下的楼层数 + 1(当前这层楼)。
根据这个特点,可以写出下面的状态转移方程:
dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1
dp[k][m - 1] 就是楼上的楼层数,因为鸡蛋个数 k 不变,也就是鸡蛋没碎,扔鸡蛋次数 m 减一;
dp[k - 1][m - 1] 就是楼下的楼层数,因为鸡蛋个数 k 减一,也就是鸡蛋碎了,同时扔鸡蛋次数 m 减一。
上述递推公式可以这样理解,一次扔鸡蛋至少能推测1层楼,剩余m-1次扔鸡蛋则分别可以推测dp[k-1][m-1]和dp[k][m-1]层楼
第三种DP方法确实看不懂,太高级了,我就学第二种吧哈哈哈哈。
回到蓝桥杯这道题,就相当于鸡蛋数=3,楼层数=1000。
答案:19
五、程序填空题
六、递增三元组(模拟、双指针)
直接暴力,能拿62分。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] a = new int[n];
int[] b = new int[n];
int[] c = new int[n];
for (int i = 0; i < n; i++) {
a[i] = scan.nextInt();
}
for (int i = 0; i < n; i++) {
b[i] = scan.nextInt();
}
for (int i = 0; i < n; i++) {
c[i] = scan.nextInt();
}
int ans = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k < n; k++) {
if (a[i] < b[j] && b[j] < c[k]) {
ans++;
}
}
}
}
System.out.println(ans);
}
}
想想优化方法,题目没有要求i、j、k顺序,可以先把ABC三个数组排序,然后依次遍历三个数,第三个数可以用二分来找。得分72,还是超时了。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] a = new int[n];
int[] b = new int[n];
int[] c = new int[n];
for (int i = 0; i < n; i++) {
a[i] = scan.nextInt();
}
for (int i = 0; i < n; i++) {
b[i] = scan.nextInt();
}
for (int i = 0; i < n; i++) {
c[i] = scan.nextInt();
}
Arrays.sort(a);
Arrays.sort(b);
Arrays.sort(c);
int ans = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (b[j] <= a[i]) {
continue;
}
int left = 0;
int right = n;
int mid;
// 找第一个大于b[j]的元素
while (left < right) {
mid = left + (right - left) / 2;
if (c[mid] > b[j]) {
right = mid;
} else {
left = mid + 1;
}
}
// 没找到
if (left == n) {
break;
}
// 找到了,c中left及left之后的元素都能大于b[j]
ans += n - left;
}
}
System.out.println(ans);
}
}
考虑用数学方法来缩短时间。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] a = new int[n];
int[] b = new int[n];
int[] c = new int[n];
for (int i = 0; i < n; i++) {
a[i] = scan.nextInt();
}
for (int i = 0; i < n; i++) {
b[i] = scan.nextInt();
}
for (int i = 0; i < n; i++) {
c[i] = scan.nextInt();
}
Arrays.sort(a);
Arrays.sort(b);
Arrays.sort(c);
long ans = 0;
int p = 0;
int q = 0;
// 以中间的数字b为依据,找a和c中满足条件的位置
for (int i = 0; i < n; i++) {
// p确定a中第一个 >= b[i]的数,那么a前面就有p个数 < b[i](注意都是排过序的)
while (p < n && a[p] < b[i]) p++;
// q确定c中第一个 > b[i]的数,那么c后面就有n - q个数 > b[i]
while (q < n && c[q] <= b[i]) q++;
// a中有p种可能,c中有q种可能,总共有p * q种可能
ans += (long) (p * (n - q));
}
System.out.println(ans);
}
}
最后一个实例死活过不了,不知道为啥,方法是对的,用c/c++就能跑过。
七、螺旋折线(模拟、找规律)

最朴素的模拟算法,从原点开始左、上、右下的移动,能拿50分。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
long x = scan.nextLong();
long y = scan.nextLong();
// 对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是
// 从原点到(X, Y)的螺旋折线段的长度
long cnt = 0;
long move = 1;
long tmpx = 0;
long tmpy = 0;
boolean flag = false;
while (flag == false) {
long tmpmove = move;
while (tmpmove > 0 && flag == false) {
// 左
tmpx--;
cnt++;
if (tmpx == x && tmpy == y) {
flag = true;
break;
}
tmpmove--;
}
tmpmove = move;
while (tmpmove > 0 && flag == false) {
// 上
tmpy++;
cnt++;
if (tmpx == x && tmpy == y) {
flag = true;
break;
}
tmpmove--;
}
// 走完左上之后,move要++
move++;
tmpmove = move;
while (tmpmove > 0 && flag == false) {
// 右
tmpx++;
cnt++;
if (tmpx == x && tmpy == y) {
flag = true;
break;
}
tmpmove--;
}
tmpmove = move;
while (tmpmove > 0 && flag == false) {
// 下
tmpy--;
cnt++;
if (tmpx == x && tmpy == y) {
flag = true;
break;
}
tmpmove--;
}
// 走完右下之后,move还要++
move++;
}
System.out.println(cnt);
}
}
上面的代码可以帮助我们找规律,我们可以先把四个点的规律找出来(很简单,自己可以试出来),发现所有点的坐标都可以从最右上角的点的长度推算出来,(1,1) = 4 (2,2) = 16 (3,3) = 36 (4,4) = 64,右上角的点的规律 = n * n * 4,其余点的位置都可以从它推算出,从而写出下面的代码:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
long x = scan.nextLong();
long y = scan.nextLong();
// 对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是
// 从原点到(X, Y)的螺旋折线段的长度
long cnt = 0;
if (x >= 0 && y >= 0) {
// 第一象限
if (y >= x) {
// 2,3
cnt = y * y * 4;
cnt = cnt - (y - x);
} else {
// 3,2
cnt = x * x * 4;
cnt = cnt + (x - y);
}
} else if (x >= 0 && y <= 0) {
// 第四象限
if (-y >= x) {
// 2,-3
// 转换成上面的情况
cnt = (-y) * (-y) * 4;
cnt = cnt + (-y) * 2;
cnt = cnt + (-y - x);
} else {
// 3,-2
cnt = x * x * 4;
cnt = cnt + x * 2;
cnt = cnt - (x + y);
}
} else if (x <= 0 && y >= 0) {
// 第二象限
if (-x >= y) {
// -3,2
cnt = (-x) * (-x) * 4;
cnt = cnt - (-x) * 2;
cnt = cnt - (-x - y);
} else {
// -2,3
cnt = y * y * 4;
cnt = cnt - y * 2;
cnt = cnt + (y + x);
}
} else if (x <= 0 && y <= 0) {
// 第三象限
if (-x >= -y) {
// -3,-2
cnt = (-y) * (-y) * 4;
cnt = cnt + 4 * (-y);
cnt = cnt + (y - x);
} else {
// -2,-3
cnt = (-y) * (-y) * 4;
cnt = cnt + 4 * (-y);
cnt = cnt - (x - y);
}
}
System.out.println(cnt);
}
}
遇到这种题,如果时间允许可以先写一个模拟代码,方便找规律,找到规律了就可以直接写出数学公式的表达代码。
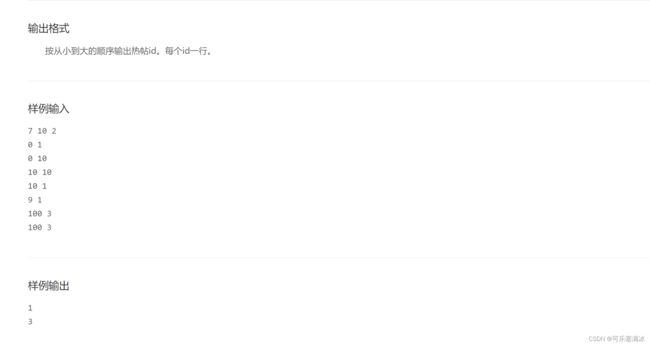
八、日志统计(排序、滑动窗口)
import java.util.*;
import java.io.*;
public class Main {
// 加速读取
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
public static void main(String[] args) throws IOException {
String[] input = in.readLine().trim().split(" ");
// 如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞
// 小明就认为这个帖子曾是”热帖”
// 所有曾是”热帖”的帖子编号。
// 在[T,T+D)区间内
int n = Integer.parseInt(input[0]);
int d = Integer.parseInt(input[1]);
int k = Integer.parseInt(input[2]);
ArrayList<Integer>[] idTime = new ArrayList[100001];
for (int i = 0; i < 100001; i++) {
idTime[i] = new ArrayList<>();
}
int[] ids = new int[n + 1];
for (int i = 0; i < n; i++) {
input = in.readLine().trim().split(" ");
int ts = Integer.parseInt(input[0]);
int id = Integer.parseInt(input[1]);
idTime[id].add(ts);
ids[i] = id;
}
Arrays.sort(ids);
for (int i = 0; i < n; i++) {
// 去重
if (i > 0 && ids[i] == ids[i - 1]) continue;
ArrayList<Integer> tmp = idTime[ids[i]];
// 时间从小到大
Collections.sort(tmp);
int j = 0;
int kk = 0;
int cnt = 0;
while (kk < tmp.size() && j <= kk) {
if (tmp.get(kk) - tmp.get(j) < d) {
cnt++;
if (cnt >= k) {
System.out.println(ids[i]);
break;
} else {
// 右移指针
kk++;
}
} else {
j++;
// 别忘了右指针也要拿回来!
kk = j;
cnt = 0;
}
}
}
}
}
上面这个给出的不是双指针,因为如果超出了时间间隔,我还让右指针跑回来了,存粹地说,就是暴力枚举。
下面这个写法才是双指针(或者说滑动窗口,因为实质是在维护一个滑动窗口):
import java.util.*;
import java.io.*;
class node {
int ts, id;
node() {};
node(int ts, int id) {
this.ts = ts;
this.id = id;
}
}
public class Main {
// 加速读取
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
public static void main(String[] args) throws IOException {
String[] input = in.readLine().trim().split(" ");
// 如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞
// 小明就认为这个帖子曾是”热帖”
// 所有曾是”热帖”的帖子编号。
// 在[T,T+D)区间内
int n = Integer.parseInt(input[0]);
int d = Integer.parseInt(input[1]);
int k = Integer.parseInt(input[2]);
node[] nodes = new node[n];
for (int i = 0; i < n; i++) {
input = in.readLine().trim().split(" ");
int ts = Integer.parseInt(input[0]);
int id = Integer.parseInt(input[1]);
nodes[i] = new node(ts, id);
}
// 按时间从小到大排序
Arrays.sort(nodes, new Comparator<node>() {
@Override
public int compare(node o1, node o2) {
return o1.ts - o2.ts;
}
});
// 双指针
int i = 0;
int j = 0;
// 记录点赞数
int[] cnt = new int[100001];
boolean[] is = new boolean[100001];
while (j < n && i <= j) {
int tid = nodes[j].id;
// 获得一个赞
cnt[tid]++;
while (nodes[j].ts - nodes[i].ts >= d) {
cnt[nodes[i].id]--;
i++;
}
if (cnt[tid] >= k) {
is[tid] = true;
}
j++;
}
for (int ii = 0; ii < 100001; ii++) {
if (is[ii]) System.out.println(ii);
}
}
}
滑动窗口专题讲解+练习
九、全球变暖(DFS搜索)

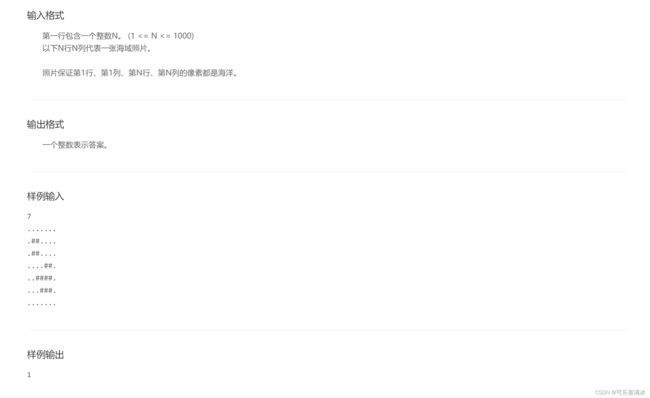
一开始想法是先统计总的岛屿数,再用for循环去掉最外层的像素,再统计岛屿数,相减就得到结果,但是太复杂了,完全可以直接统计一个岛屿的边和总和的面积,比较边和岛屿的面积是否相同,相同必被淹。(自己还是太蠢了-/-)
统计岛屿总的像素点和边的像素点,都可以在dfs中计算出,注意,因为要统计边的像素点,所以!!!不要为了省掉vis数组,而去选择通过淹没岛屿像素的方式来标记访问过的像素,如果不使用vis数组,会导致岛屿的中间像素点不能被判断出,还是会被判断为边像素点!!!这是非常严重的问题!!!
还需要注意的是,题目中已经说到,最外围一圈全都是海水!
import java.util.*;
public class Main {
static int n;
static int around;
static int total;
static char[][] map = new char[1001][1001];
static int[] xx = new int[]{-1,1,0,0};
static int[] yy = new int[]{0,0,-1,1};
static int[][] vis = new int[1001][1001];
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
n = scan.nextInt();
for (int i = 0; i < n; i++) {
// 注意字符的读入
map[i] = scan.next().toCharArray();
}
int cnt = 0;
// 第一次dfs,统计出岛屿数量
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (map[i][j] != '.' && vis[i][j] == 0) {
around = 0;
total = 0;
// 注意要使用vis数组,而不是淹没map来实现标注!!!
vis[i][j] = 1;
dfs(map, i, j);
// 边像素点数 == 整体面积像素点,则这个岛屿肯定被淹没
if (around == total) {
cnt++;
}
}
}
}
System.out.println(cnt);
}
static void dfs(char[][] map, int x, int y) {
// 当前岛屿总体的像素++
total++;
// 统计岛屿边缘像素点的时候不需要管周围是否vis过,因为你管的是当前“这个像素点”
for (int i = 0; i < 4; i++) {
// 当前岛屿边的像素++
if (map[x + xx[i]][y + yy[i]] == '.') {
around++;
break;
}
}
for (int i = 0; i < 4; i++) {
int tmpx = x + xx[i];
int tmpy = y + yy[i];
if (tmpx < 0 || tmpx >= n || tmpy < 0 || tmpy >= n || map[tmpx][tmpy] == '.' || vis[tmpx][tmpy] == 1) {
continue;
}
vis[tmpx][tmpy] = 1;
dfs(map, tmpx, tmpy);
}
}
}
之前一直统计总体岛屿面积,这一次需要统计边的像素点,做完也是收获很大。(当然BFS也可以做,一样的道理)
十、堆的计数
数据结构相关的问题,还没有具体练习,先放在这里…(后面学了更)
2018年整体难度都很大,填空题难度大,编程题难度也大,没有那种很水的题,都是需要写一定时间的。