java二叉树堆栈遍历_二叉树的各种遍历方式,我都帮你总结了,附有队列堆栈图解...
今天我来分享一篇关于二叉树的文章(建议收藏,便于巩固基础)。
看完此文leetcode至少解决八道题
掌握二叉树的前序、中序、后序遍历以及两种不同的实现方式:递归与非递归
非递归时遍历与层次遍历时,有详细的图解表示队列/栈中的元素是如何移动的,有助于理解代码的运行
二叉树介绍
二叉树(binary tree) 是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。
二叉树的递归定义为: 二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树
逻辑上二叉树有
五种基本形态,如图所示空二叉树
只有一个根结点的二叉树
只有左子树
完全二叉树
只有右子树
二叉树相关属性解释:
结点:包含一个数据元素及若干指向子树分支的信息。
结点的度:一个结点拥有子树的数目称为结点的度。
叶子结点:也称为终端结点,没有子树的结点或者度为零的结点。
分支结点:也称为非终端结点,度不为零的结点称为非终端结点。
树的度:树中所有结点的度的最大值。
结点的层次:从根结点开始,假设根结点为第1层,根结点的子节点为第2层,依此类推,如果某一个结点位于第L层,则其子节点位于第L+1层。
树的深度:也称为树的高度,树中所有结点的层次最大值称为树的深度。
有序树:如果树中各棵子树的次序是有先后次序,则称该树为有序树。
无序树:如果树中各棵子树的次序没有先后次序,则称该树为无序树。
二叉树遍历方式
二叉树遍历方式分为三种
前序遍历(根左右):访问根结点,再访问左子树、再访问右子树。
中序遍历(左根右):先访问左子树,再访问根结点、再访问右子树。
后续遍历(左右根):先访问左子树,再访问右子树,再访问根结点。
例如一个这个样子的二叉树,按三种遍历方法分别遍历,输出的结果分别是
前序遍历:ABDECFG
中序遍历:DBEAFCG
后续遍历:DEBFGCA
下面我们一起来用代码实现下这三种遍历
注:以上
前序、中序、后序每一种遍历方式都有
递归和
非递归两种实现方法
前序遍历就是
深度优先遍历(DFS)
层次遍历就是
广度优先遍历(BFS)
二叉树递归遍历
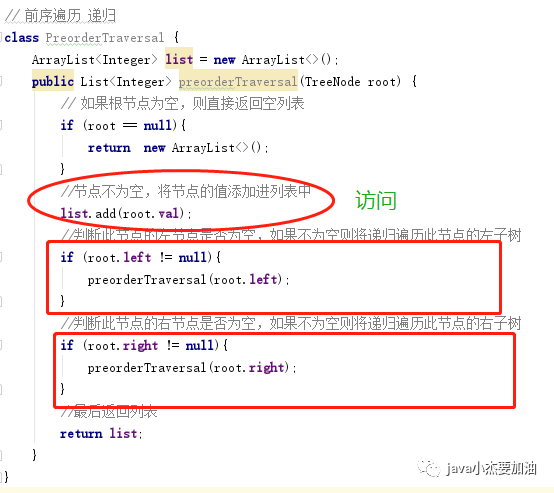
* 前序遍历 (LeetCode 144)
class Solution{
//声明列表
ArrayList list = new ArrayList<>();
public List preorderTraversal(TreeNode root){
// 如果根节点为空,则直接返回空列表
if (root == null){
return new ArrayList<>();
}
//节点不为空,将节点的值添加进列表中
list.add(root.val);
//判断此节点的左节点是否为空,如果不为空则将递归遍历左子树
if (root.left != null){
preorderTraversal(root.left);
}
//判断此节点的右节点是否为空,如果不为空则将递归遍历右子树
if (root.right != null){
preorderTraversal(root.right);
}
//最后返回列表
return list;
}
}
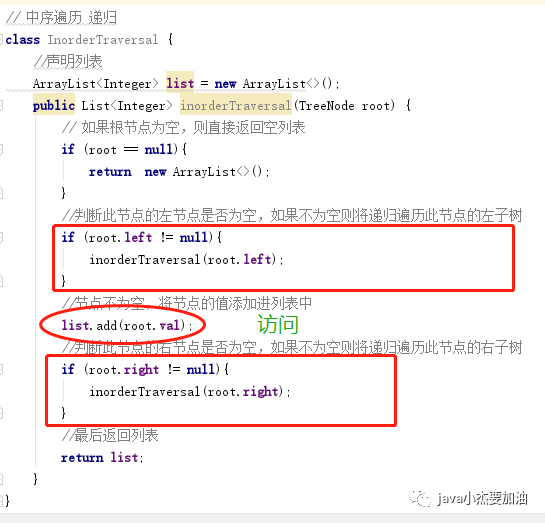
中序遍历(LeetCode 94)
class Solution{
//声明列表
ArrayList list = new ArrayList<>();
public List inorderTraversal(TreeNode root){
// 如果根节点为空,则直接返回空列表
if (root == null){
return new ArrayList<>();
}
//判断此节点的左节点是否为空,如果不为空则将递归遍历此节点的左子树
if (root.left != null){
inorderTraversal(root.left);
}
//节点不为空,将节点的值添加进列表中
list.add(root.val);
//判断此节点的右节点是否为空,如果不为空则将递归遍历此节点的右子树
if (root.right != null){
inorderTraversal(root.right);
}
//最后返回列表
return list;
}
}
后续遍历(LeetCode 145)
class Solution{
//声明列表
ArrayList list = new ArrayList<>();
public List postorderTraversal(TreeNode root){
// 如果根节点为空,则直接返回空列表
if (root == null){
return new ArrayList<>();
}
//判断此节点的左节点是否为空,如果不为空则将递归遍历此节点的左子树
if (root.left != null){
postorderTraversal(root.left);
}
//判断此节点的右节点是否为空,如果不为空则将递归遍历此节点的右子树
if (root.right != null){
postorderTraversal(root.right);
}
//节点不为空,将节点的值添加进列表中
list.add(root.val);
//最后返回列表
return list;
}
}
我们通过观察发现,这代码怎么这么像,是的就是很像,他们唯一的区别就是list.add(root.val);代码的位置不一样,这行代码就代表文中的 遍历(访问)
下图中为前序遍历(根左右)
下图中为后序遍历(左右根)
二叉树非递归遍历
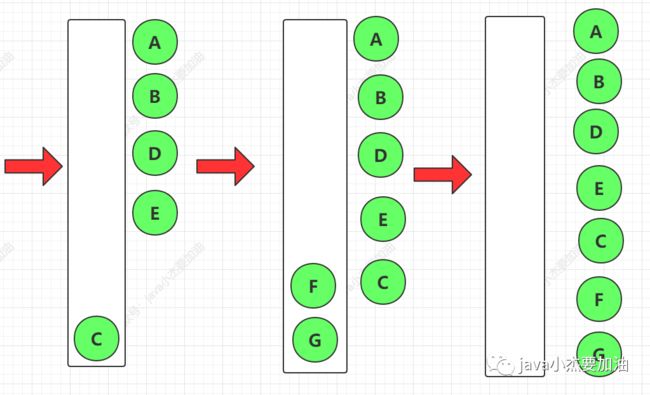
用到栈(FILO 先进后出的特性)
每段代码后,都有栈和其中元素的关系具体过程,建议静下心来慢慢看,有助于理解代码如何运行
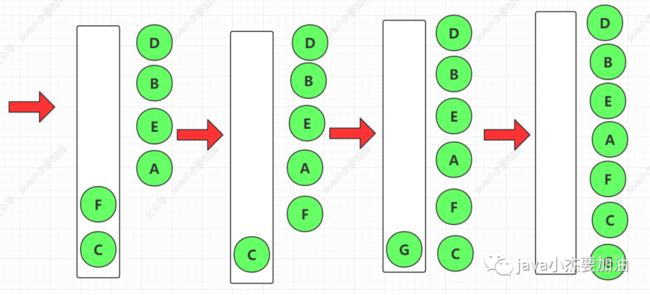
前序遍历
class Solution{
List list = new ArrayList();
public List preorderTraversal(TreeNode root){
//如果根节点为空,则直接返回空列表
if(root==null){
return new ArrayList();
}
//声明一个栈
Stack stack = new Stack<>();
//将节点入栈
stack.push(root);
//如果栈不为空
while (!stack.empty()){
//从栈弹出这个节点
TreeNode node = stack.pop();
//添加进列表中
list.add(node.val);
// 如果这个节点的右子节点不为空
if (node.right!=null){
// 将其入栈 因为栈是先进后出,所以先压栈右子节点 后出
stack.push(node.right);
}
// 如果这个节点的左子节点不为空
if (node.left!=null){
// 将其入栈 因为栈是先进后出,所以后压栈左子节点 先出
}
}
//返回列表
return list;
}
}
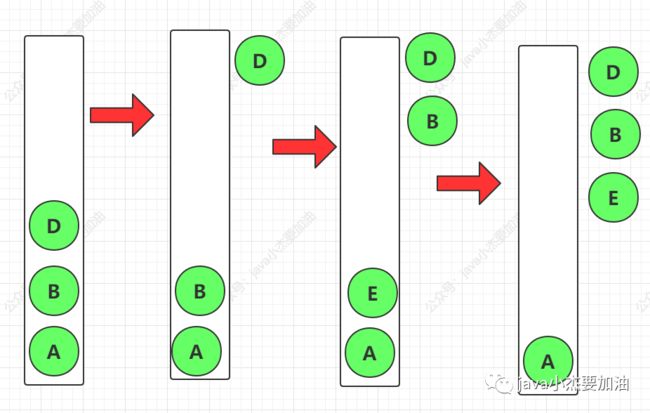
中序遍历
class Solution{
public List inorderTraversal(TreeNode root){
//判断节点是否为空,为空的话直接返回空列表
if (root == null){
return new ArrayList();
}
//声明列表存储结果
List list = new ArrayList();
//声明一个栈
Stack stack = new Stack<>();
//当节点不为空或者栈不为空时
while (root != null || !stack.empty()){
//当节点不为空时
while (root != null){
//将节点压栈
stack.push(root);
//将节点指向其左子节点
root = root.left;
}
//如果栈不为空
if (!stack.empty()){
//将栈里元素弹出来
TreeNode node = stack.pop();
//添加进列表中
list.add(node.val);
//将节点指向其右子节点
root = node.right;
}
}
return list;
}
}
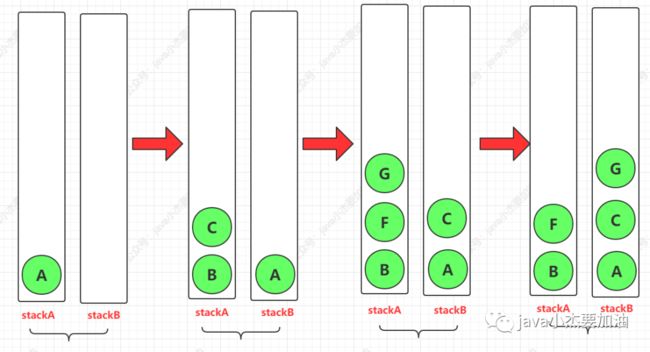
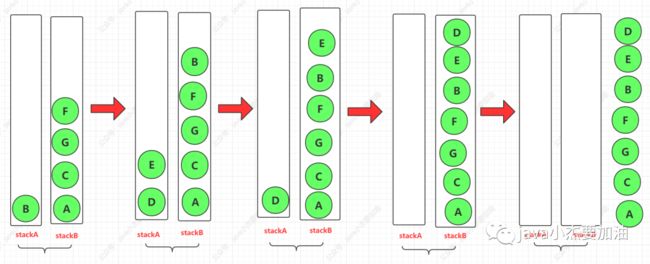
后序遍历
class Solution{
public List postorderTraversal(TreeNode root){
// 如果根节点为空,则直接返回空列表
if (root == null){
return new ArrayList<>();
}
//声明列表
ArrayList list = new ArrayList<>();
//声明栈A
Stack stackA = new Stack();
//声明栈B
Stack stackB = new Stack();
//将次元素压入栈A
stackA.push(root);
//当栈A不为空时
while (!stackA.empty()){
//取出其中压入的元素
TreeNode node = stackA.pop();
//压入栈B中
stackB.push(node);
//当此节点左子节点不为空时
if (node.left != null){
//压入栈A
stackA.push(node.left);
}
//当此节点右子节点不为空时
if (node.right != null){
//压入栈A
stackA.push(node.right);
}
}
//当栈B不为空时
while (!stackB.empty()){
//取出其元素并且添加至列表中
TreeNode node = stackB.pop();
list.add(node.val);
}
//最后返回列表
return list;
}
}
二叉树层序遍历(BFS)
LeetCode 102 二叉树的层序遍历
用到队列(FIFO 先进先出的特性)代码后有队列和其中元素的关系具体过程,建议静下心来慢慢看,有助于理解代码如何运行
class Solution{
public List> levelOrder(TreeNode root) {
if (root == null) {
return new ArrayList>();
}
// 声明一个列表存储每一行的数据
List> result = new ArrayList<>();
//声明一个队列
LinkedList queue = new LinkedList<>();
//如果根节点不为空,将其入队
queue.offer(root);
//当队列不为空时,代表队列里有数据
while (!queue.isEmpty()) {
//存储每一行的数据line
List line = new ArrayList();
//保存队列中现有数据的个数,这些就是要添加至每一行列表的值
int size = queue.size();
for (int i=0;i
//取出队列的节点 (FIFO 先进先出)
TreeNode node = queue.poll();
line.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
result.add(line);
}
return result;
}
}
leetcode二叉树相关练习
我们看到了这里,对二叉树的前序(DFS)、中序、后序、递归/非递归以及层次遍历(BFS)都有了一定的了解(
如果上面的图都消化了的话)
然后我们趁热打铁来几道leetcode题目试试手!(总体代码和上面只有稍微的改动,因为大致思想是一样的,把上面的内容都消化了的话就很简单啦)
leetcode-257 二叉树的所有路径
class Solution{
public List binaryTreePaths(TreeNode root){
if (root == null){
return new ArrayList<>();
}
ArrayList list = new ArrayList<>();
Stack stack = new Stack();
//这个栈存储路径,与上一个存储节点的栈一样的操作
Stack path = new Stack();
stack.push(root);
path.push(root.val+"");
while (!stack.empty()){
TreeNode node = stack.pop();
String p = path.pop();
//当是叶子节点的时候,此时栈中的路径即为一条完整的路径,可以加入到结果中
if (node.right == null && node.left == null ){
list.add(p);
}
//如果右子节点不为空
if (node.right != null){
stack.push(node.right);
//将临时路径继续压栈
path.push(p+"->"+node.right.val);
}
//如果左子节点不为空
if (node.left != null){
stack.push(node.left);
//将临时路径继续压栈
path.push(p+"->"+node.left.val);
}
}
return list;
}
}
leetcode-104 二叉树的最大深度 与 剑指offer 55-I 相同
class Solution{
public int maxDepth(TreeNode root){
if (root == null){
return 0;
}
LinkedList queue = new LinkedList<>();
int result = 0;
queue.offer(root);
while (!queue.isEmpty()){
//层数+1
result++;
//这是当前层的节点的个数
int size = queue.size();
for (int i=0;i
//要将其全部出队后,才可以再次计数
TreeNode node = queue.poll();
if (node.left != null){
//如果出队的节点还有左子节点,就入队
queue.offer(node.left);
}
if (node.right != null){
//如果出队的节点还有右子节点,就入队
queue.offer(node.right);
}
}
}
//返回层数
return result;
}
}
leetcode-107 二叉树的层序遍历2
class Solution{
public List> levelOrderBottom(TreeNode root) {
if (root == null){
return new ArrayList>() ;
}
List> result = new ArrayList>() ;
LinkedList queue = new LinkedList<>();
//声明一个栈,用来存储每一层的节点
Stack > stack = new Stack<>();
queue.offer(root);
while (!queue.isEmpty()){
int size = queue.size();
ArrayList list = new ArrayList<>();
for (int i=0;i
TreeNode node = queue.poll();
list.add(node.val);
if (node.left != null){
queue.offer(node.left);
}
if (node.right != null){
queue.offer(node.right);
}
}
//将这一层的节点压入栈中
stack.push(list);
}
//当栈不为空时,弹出结果,从而达到从下往上遍历二叉树的效果
while (!stack.isEmpty()){
ArrayList list = stack.pop();
result.add(list);
}
return result;
}
}
推荐关注