图 —— 最短路径(一)Dijkstra算法
目录
- 1、最短路径概念
- 2、Dijkstra最短路算法图解
- 3、求最短路径的简单代码
- (1)如果要求打印出指定起点到其他各点的最短路径长度
- (2)如果要求打印出指定起点到其他各点的最短路径 即连路径也要打印出来
1、最短路径概念
最短路径就是图中两点之间经过的最短距离(就是最小权值),图必须是带有权值的,可以是无向可以是有向的,
算法具体的形式包括:
- 确定起点的最短路径问题:即已知起始结点,求最短路径的问题。适合使用Dijkstra算法。
- 确定终点的最短路径问题:与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
- 确定起点终点的最短路径问题:即已知起点和终点,求两结点之间的最短路径。
- 全局最短路径问题:求图中所有的最短路径。适合使用Floyd-Warshall算法。
主要介绍以下几种算法:
- Dijkstra最短路算法(单源最短路);
- Bellman–Ford算法(解决负权边问题);
- Floyd最短路算法(全局/多源最短路);
这一节主要说Dijkstra算法;其他两种算法地址→图 —— 最短路径(二)
2、Dijkstra最短路算法图解
迪科斯彻算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块。
dijkstra算法本质上算是贪心的思想,每次在剩余节点中找到离起点最近的节点放到队列中,并用来更新剩下的节点的距离,再将它标记上表示已经找到到它的最短路径,以后不用更新它了。这样做的原因是到一个节点的最短路径必然会经过比它离起点更近的节点,而如果一个节点的当前距离值比任何剩余节点都小,那么当前的距离值一定是最小的。(剩余节点的距离值只能用当前剩余节点来更新,因为求出了最短路的节点之前已经更新过了)
dijkstra就是这样不断从剩余节点中拿出一个可以确定最短路径的节点最终求得从起点到每个节点的最短距离。
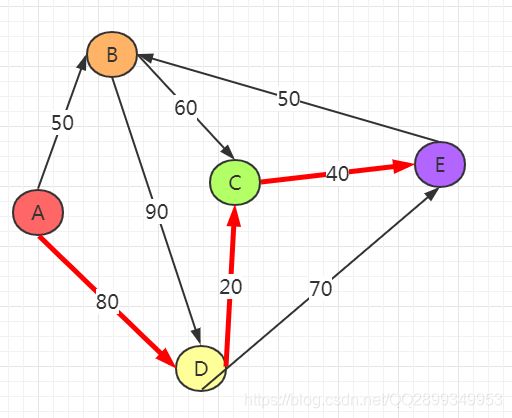
上图中A→E的最短路径是:
先定义一个节点类,用来存放图节点:
/**
* @ClassName: Node
* @Author: lzq
* @Date: 2019/08/23 07:33
* @Description: 图节点
*/
public class Node {
public T name; //记录当前节点的名字
public boolean sign; //遍历标志
public Node(T name) {
this.name = name;
this.sign = false;
}
}
再定义一个类用来存放上一个节点到当前节点的距离以及上一个节点的位置,以便于最后打印路径:
/**
* @ClassName: Distance
* @Author: lzq
* @Date: 2019/08/23 07:37
* @Description: 记录从上一个节点到当前节点的距离
*/
public class Distance {
public int par; //上一个节点的下标 用数组储存节点的,记录下标即可
public int distance; //从上一个节点到当前节点的距离
public Distance(int par,int distance) {
this.par = par;
this.distance = distance;
}
}
接着是一个表示图的类,先定义以下属性,以及构造函数:
/**
* @ClassName: Graph
* @Author: lzq
* @Date: 2019/08/23 07:41
* @Description: 图
*/
public class Graph {
private int maxNodeNumber = 10; //每个节点的最大指针数量,也指图的最多节点数量,可以根据需要调整
private int INF = 65535; //表示两个节点之间不相通,它们的距离就是INF
private Node[] nodes; //节点数组,每个图节点放在这个数组里面
private int[][] disIJ; //表示两点之间的距离 二维数组的横纵坐标表示对应的起点、终点节点,值表示距离
private Distance[] sPath; //用来记录以当前起点到各个节点的距离,不停的更新它用来获取最短路径,这个就是用来储存最短路径的
private int count; //总的节点数量
private int n; //遍历过的节点数量
private int start; //最初的起点
private int isStart; //当前起点下标
private int startToCurDis; //从开始节点到当前节点的距离,最短路径的核心算法会用
//初始化相关变量
public Graph() {
this.nodes = new Node[maxNodeNumber]; //假设最多十个节点
this.disIJ = new int[maxNodeNumber][maxNodeNumber];
this.sPath = new Distance[maxNodeNumber];
this.count = 0;
this.n = 0;
//初始化各节点之间的距离
for (int i = 0; i < maxNodeNumber; i++) {
for (int j = 0; j < maxNodeNumber; j++) {
this.disIJ[i][j] = INF;
}
}
}
在构造函数里面创建数组、以及初始化数组之后:
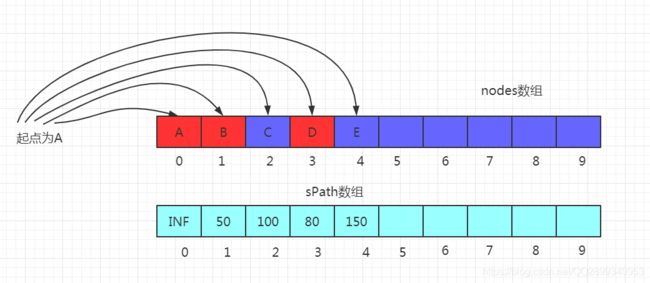
nodes数组:
disIJ数组:
sPath数组:
添加节点、赋权值:
/**
* 添加节点名字
* @param name
*/
public void addNodeName(T name) {
this.nodes[n++] = new Node<>(name);
}
/**
* 给节点赋权值
* @param start
* @param end
* @param weight
*/
public void addNodeWeight(int start,int end,int weight) {
this.disIJ[start][end] = weight;
}
当我们调用上述两个方法将上面示意图中的节点和权值给进去之后:
nodes数组:

disIJ数组(我把下标对应的元素放在旁边了,还有用到的节点拿特殊颜色标出来了,便于观察):
Dijkstra算法代码:
/**
* 没有指定起点的话,默认从0开始,一般都是这个
*/
public void dijkstra() {
dijkstra1(0);
}
/**
* 指定起点
* @param startNodeIndex
*/
public void dijkstra1(int startNodeIndex) {
if(startNodeIndex >= n || startNodeIndex < 0) {
return;
}
start = startNodeIndex;
isStart = startNodeIndex; //起点
nodes[isStart].sign = true; //更改遍历标记,标记被遍历过了
count++; //遍历过的节点数+1
//初始化sPath数组
for (int i = 0; i < n; i++) {
int dis = disIJ[isStart][i]; //获取起点到当前节点的距离
sPath[i] = new Distance(isStart,dis); //赋值给sPath
}
//开始寻找最短路径,直到每个节点都标记过了
while (count < n) {
int startToCurMin = getstartToCurMin(); //找到距离当前起点最近的邻接节点位置
int dis = sPath[startToCurMin].distance; //通过位置拿到距离当前起点以及最近节点之间的距离
if(dis == INF) {
//两点不通,直接跳出,意思就是没有以当前起点最近的节点,
break;
}else {
isStart = startToCurMin; //更新起点
startToCurDis = sPath[isStart].distance; //从最初的起点到新的起点之间的距离
}
nodes[isStart].sign = true; //更新标记
count++;
adjustMinPath(); //核心算法,更新最短路径
}
clearSign();
}
/**
* 清除标记
*/
private void clearSign() {
count = 0;
for (int i = 0; i < n; i++) {
nodes[i].sign = false;
}
}
/**
* 求最短路径的核心算法
*/
private void adjustMinPath() {
int tempCount = 0; //表示当前节点
while (tempCount < n) {
if(nodes[tempCount].sign || tempCount == isStart) {
//当前节点找过了或者当前节点是起点自己,直接跳过
tempCount++;
continue;
}
int curStartToCur = disIJ[isStart][tempCount]; //拿到当前起点到当前节点的距离
int startToCur = startToCurDis+curStartToCur; //最初的那个起点到当前节点的距离,最大不超过INF
int sPathDist = sPath[tempCount].distance; //获取已记录的最初起点到当前节点的距离
if(startToCur < sPathDist) { //如果已记录的值大于刚得到的新值,更新
sPath[tempCount].distance = startToCur; //更新当前节点到最初起点之间的距离
sPath[tempCount].par = isStart; //更新它的父节点
}
tempCount++;
}
}
/**
* 找到距离当前起点最近的邻接节点,返回该节点的下标
* @return
*/
private int getstartToCurMin() {
int disMin = INF; //默认距离当前起点的最近的相邻起点的最短距离
int index = isStart; //距离当前起点最近的相邻节点对应的下标
//开始查找
for (int i = 0; i < n; i++) {
if(i == isStart) { //自己到自己就不用算了
continue;
}
//这个最近的相邻节点必须没有被遍历,并且距离当前节点的距离是最近的
if(!nodes[i].sign && sPath[i].distance < disMin) {
disMin = sPath[i].distance;
index = i;
}
}
return index;
}
算法流程解析:
图先拿下来:

以图中A为起点说明,下图中红色节点表示已经遍历过了:
1、当我们根据传入的数据把sPath数组初始化以后,它就变成了这个样子,A不能到自己、也不能直接到达C、E所以A与A、B、C、D、E这几个节点的距离最开始为INF、50、INF、80、INF:
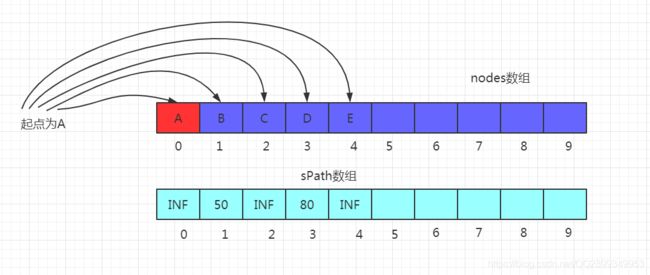
2、现在找当前起点中距离A最近的节点,也就是50,即B节点,更新这个sPath数组相关的值,得到:

3、继续找距离A最近的节点,这个时候没有被遍历的节点只有C、D、E所以要在C、D、E里面找,最终找到D,那么以D为起点,更新这个sPath数组相关的值;
4、继续找距离A最近的节点,这个时候要在C、E里面找,我们找到C,以C为新的起点,继续更新sPath:
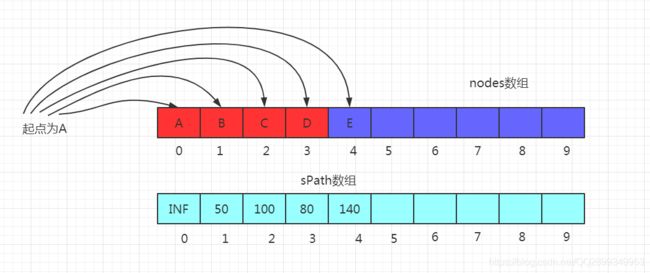
5、继续,只剩E了,以E为起点,更新sPath数组,所有节点遍历完了,这就找到所有从A出发到达各节点之间的最短路径了:

可以按需要打印,修改下面两个方法就好:
/**
* 打印最短路径
*/
public void show() {
System.out.println("起点为"+nodes[start].name+":");
for (int i = 0; i < n; i++) {
System.out.print("到达"+nodes[i].name+"距离为:\t");
if(sPath[i].distance == INF) {
System.out.println("INF");
continue;
}else {
System.out.print(sPath[i].distance+"\t");
}
dgPrint(i);
System.out.println();
}
System.out.println();
}
/**
* 递归打印路径
* @param par
*/
private void dgPrint(int par) {
if(par == start) {
System.out.print(nodes[par].name);
return;
}
dgPrint(sPath[par].par);
System.out.print("-->"+nodes[par].name);
}
}
测试代码:
public static void main(String[] args) {
Graph graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addEdge(0,1,50); //A-->B 50
graph.addEdge(0,3,80); //A-->D 80
graph.addEdge(1,2,60); //B-->C 60
graph.addEdge(1,3,90);
graph.addEdge(2,4,40);
graph.addEdge(3,2,20);
graph.addEdge(3,4,70);
graph.addEdge(4,1,50);
graph.dijkstra(); //起点为A
graph.dijkstra1(2); //以C为起点
}
好了,以上就是最短路径的狄杰斯特拉算法思想以及一个求最短路径长度、路径的的代码,但是在面试中是不可能有时间让你去写这么多代码的,一般写一个方法就够了,下面就是对应的单个方法求最短路径;
3、求最短路径的简单代码
(1)如果要求打印出指定起点到其他各点的最短路径长度
因为在大部分面试题的的图相关的编程题都是给的一个关系矩阵,并且节点自己到自己的距离一般为0、不可达节点之间的距离为-1,上面例子中为了便于理解这些关系我都拿INF表示了,那么如果在面试题中碰到这种编程题,用下面这种写法就好,数组的下标对应相应的图节点,传入的是起始节点下标以及一个表示各个节点之间的权值、方向的数组,返回的是一个表示起始节点到各节点的最短路径的数组,当然也可以根据题目需要做适当修改,核心代码就这个:
/**
* 求最短路径的方法 这个方法返回一个数组,里面是每个节点到起点之间的最短路径
* @param startIndex 起始节点
* @param disIJ 给出的矩阵数组 表示各个节点之间的权值
* @return 表示起始节点到各个节点的最短路径长度的数组
*/
public static int[] dijkstra(int startIndex,int[][] disIJ) {
boolean[] sign = new boolean[disIJ.length]; //用来表示该位置的元素是否被遍历,默认全是false
int[] dis = new int[disIJ.length]; //记录每个节点到起点之间的距离
int tempStart = 0; //临时起点
int startToTempStart = 0; //最初起点到临时起点之间的距离
//初始化dis数组
for (int i = 0; i < disIJ[startIndex].length; i++) {
dis[i] = disIJ[startIndex][i];
}
sign[startIndex] = true;
int count = 0; //计数器,记录有多少个节点被遍历过了,当所有节点都被遍历完了就结束了
while (count < disIJ.length) {
//每次进来第一步:查找dis数组里面距离起点最近的那个节点
int minValue = Integer.MAX_VALUE;
int index = startIndex;
for(int i = 0;i < dis.length;i++) {
if(!sign[i] && dis[i] != -1 && dis[i] < minValue ) {
minValue = dis[i];
index = i;
}
}
if(minValue == Integer.MAX_VALUE) { //没找到,就是没有,直接退出
break;
}else {
tempStart = index;
startToTempStart = minValue;
}
sign[tempStart] = true;
count++;
//更新数组中的值
for (int i = 0; i < disIJ.length; i++) {
//如果这个节点遍历过了或者是当前起点直接跳过
if(sign[i] || i == tempStart) {
continue;
}
int tempStartToCur = disIJ[tempStart][i]; //拿到当前起点到当前节点的距离
if(tempStartToCur == -1) {
//这两点不通,跳过
continue;
}
int startIndexToCur = startToTempStart+tempStartToCur; //得到最初起点到当前节点的距离
int disStartIndexToCur = dis[i]; //获取原来记录的这两个点之间的距离
if((disStartIndexToCur == -1 && startIndexToCur > 0) || (disStartIndexToCur != -1 && disStartIndexToCur > startIndexToCur)) {
dis[i] = startIndexToCur;
}
}
}
return dis;
}
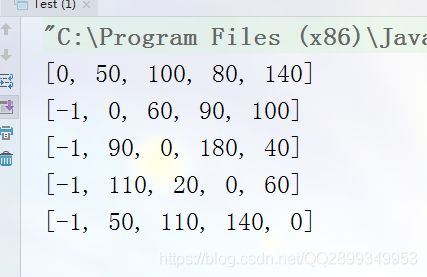
我们还是用上面的图例来测试一下这个代码:
public static void main(String[] args) {
int[][] disIJ = {{0,50,-1,80,-1},
{-1,0,60,90,-1},
{-1,-1,0,-1,40},
{-1,-1,20,0,70},
{-1,50,-1,-1,0}};
System.out.println(Arrays.toString(dijkstra(0,disIJ)));
System.out.println(Arrays.toString(dijkstra(1,disIJ)));
System.out.println(Arrays.toString(dijkstra(2,disIJ)));
System.out.println(Arrays.toString(dijkstra(3,disIJ)));
System.out.println(Arrays.toString(dijkstra(4,disIJ)));
}
(2)如果要求打印出指定起点到其他各点的最短路径 即连路径也要打印出来
我们在上面图解阶段用的是一个Distance类专门记录距离和是从哪个父节点过来的,打印的时候从这个父节点往上找就是了,所以如果题目要求需要打印路径的话,我们需要在上面方法添加一个用来记录路径的数组:
注意,有 // =========================== 就是如果需要打印路径的话,需要添加或修改代码的地方:
/**
* 求最短路径的方法 这个方法返回一个数组,里面是每个节点到起点之间的最短路径
* @param startIndex 起始节点
* @param disIJ 给出的矩阵数组 表示各个节点之间的权值
* @return 返回一个二维数组,0号下标数组表示起始节点到各个节点的最短路径长度,1号下标数组
* 表示起始节点到各个节点的最短路径 记录的是父节点下标 我们可以根据它得到最短路径
*/
public static int[][] dijkstra(int startIndex,int[][] disIJ) {
boolean[] sign = new boolean[disIJ.length]; //用来表示该位置的元素是否被遍历,默认全是false
int[] dis = new int[disIJ.length]; //记录每个节点到起点之间的距离
// 用来记录路径,数组下标表示当前节点位置,对应元素值表示父节点位置
int[] path = new int[disIJ.length]; // ===========================
int tempStart = 0; //临时起点
int startToTempStart = 0; //最初起点到临时起点之间的距离
//初始化dis数组、初始化path数组
for (int i = 0; i < disIJ[startIndex].length; i++) {
dis[i] = disIJ[startIndex][i];
//初始化每个节点的父节点,把他们都出初始化成起始节点
path[i] = startIndex; // ===========================
}
sign[startIndex] = true;
int count = 0; //计数器,记录有多少个节点被遍历过了,当所有节点都被遍历完了就结束了
while (count < disIJ.length) {
//每次进来第一步:查找dis数组里面距离起点最近的那个节点
int minValue = Integer.MAX_VALUE;
int index = startIndex;
for(int i = 0;i < dis.length;i++) {
if(!sign[i] && dis[i] != -1 && dis[i] < minValue ) {
minValue = dis[i];
index = i;
}
}
if(minValue == Integer.MAX_VALUE) { //没找到,就是没有,直接退出
break;
}else {
tempStart = index;
startToTempStart = minValue;
}
sign[tempStart] = true;
count++;
//更新数组中的值
for (int i = 0; i < disIJ.length; i++) {
//如果这个节点遍历过了或者是当前起点直接跳过
if(sign[i] || i == tempStart) {
continue;
}
int tempStartToCur = disIJ[tempStart][i]; //拿到当前起点到当前节点的距离
if(tempStartToCur == -1) {
//这两点不通,跳过
continue;
}
int startIndexToCur = startToTempStart+tempStartToCur; //得到最初起点到当前节点的距离
int disStartIndexToCur = dis[i]; //获取原来记录的这两个点之间的距离
if((disStartIndexToCur == -1 && startIndexToCur > 0) || (disStartIndexToCur != -1 && disStartIndexToCur > startIndexToCur)) {
dis[i] = startIndexToCur;
//更新这个节点的父节点,能进这个语句,肯定换了父节点
path[i] = tempStart; // ===========================
}
}
}
return new int[][] {dis,path}; // ===========================
}
测试代码:
public static void main(String[] args) {
int[][] disIJ = {{0,50,-1,80,-1},
{-1,0,60,90,-1},
{-1,-1,0,-1,40},
{-1,-1,20,0,70},
{-1,50,-1,-1,0}};
int[][] disAndPath = dijkstra(0,disIJ);
System.out.println(Arrays.toString(disAndPath[0]));
System.out.println(Arrays.toString(disAndPath[1]));
//打印以指定起点到达每个节点的最短路径 这里用数组下标表示的路径
// 如果需要字符表示的话添加一个字符数组打印对应位置的字符就好
for (int i = 0; i < disAndPath[1].length; i++) {
dfs(disAndPath[1],0,i);
System.out.println();
}
}
/**
* 递归打印路径
* @param disAndPath
* @param startIndex
* @param index
*/
private static void dfs(int[] disAndPath,int startIndex,int index) {
if(index == startIndex) {
System.out.print(index);
return;
}
dfs(disAndPath,startIndex,disAndPath[index]);
System.out.print("-->"+index);
}