RSA算法实现与体会2021-06-20

一、目的
通过学习RSA算法的基本原理，设计RSA非对称加密算法，依据现有条件，实现RSA加密算法，并对算法进行测试，最后进行总结。

二、预备知识
(一)非对称加密
非对称加密算法（asymmetric cryptographic algorithm）又名“公开密钥加密算法”。非对称加密算法需要两个密钥：公开密钥（publickey）和私有密钥（privatekey）。公开密钥与私有密钥是一对，如果用公开密钥对数据进行加密，只有用对应的私有密钥才能解密；如果用私有密钥对数据进行加密，那么只有用对应的公开密钥才能解密。因为加密和解密使用的是两个不同的密钥，所以这种算法叫作非对称加密算法。

(二)RSA简介
RSA是第一个比较完善的公开密钥算法，它既能用于加密，也能用于数字签名。RSA以它的三个发明者Ron Rivest, Adi Shamir, Leonard Adleman的名字首字母命名，这个算法经受住了多年深入的密码分析，虽然密码分析者既不能证明也不能否定RSA的安全性，但这恰恰说明该算法有一定的可信性，目前它已经成为最流行的公开密钥算法。

1.RSA算法公钥与私钥的产生
假设Alice想要通过一个不可靠的媒体接收Bob的一条私人讯息。她可以用以下的方式来产生一个公钥和一个私钥：
（1）随机选择两个大的质数p和q，p不等于q；
（2）计算N=p*q，N的长度就是密钥长度，一般指二进制长度；
（3）根据欧拉函数，求得r=(p-1)(q-1)；
（4）随机选择一个小于 r 的整数 e，且r与e互质。求得 e 关于模 r 的模反元素，命名为d；
（5）将 p 和 q 的记录销毁。
（6）(N,e)是公钥，(N,d)是私钥。
Alice将她的公钥(N,e)传给Bob，而将她的私钥(N,d)藏起来。

2.加密消息
假设Bob想给Alice送一个消息m，他知道Alice产生的N和e。他使用起先与Alice约好的格式将m转换为一个小于N的整数n，比如他可以将每一个字转换为这个字的Unicode码，然后将这些数字连在一起组成一个数字。假如他的信息非常长的话，他可以将这个信息分为几段，然后将每一段转换为n。用下面这个公式他可以将n加密为c：
n^e= c(mod N)表示n^e与c关于N同于。
计算c并不复杂。Bob算出c后就可以将它传递给Alice。

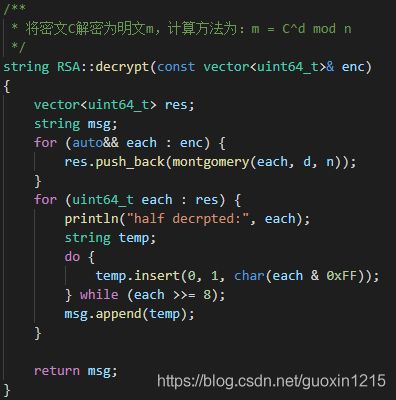
3.解密消息
Alice得到Bob的消息c后就可以利用她的密钥d来解码。她可以用以下这个公式来将c转换为n：c^d = n (mod N)得到n后，她可以将原来的信息m重新复原。

(三)数学概念
RSA加密算法中用到很多的数学概念，了解这些数学概念可以帮助我们更好的设计算法。

1.素数的概念
RSA算法首先要选取两个互不相同的质数p和q，质数的大小直接影响加密的长度和安全行。
素数是这样的整数，它除了能表示为它自己和1的乘积以外，不能表示为任何其它两个整数的乘积。例如，15＝3＊5，所以15不是素数；又如，12＝6＊2＝4＊3，所以12也不是素数。另一方面，13除了等于13＊1以外，不能表示为其它任何两个整数的乘积，所以13是一个素数。素数也称为“质数”。

2.互质数或互素数
N=pq，根据欧拉定理求出r=(p-1)(q-1),e需要与r互质且小于r。
数学教材对互质数是这样定义的：“公约数只有1的两个数，叫做互质数。”这里所说的“两个数”是指自然数。
判别方法主要有以下几种（不限于此）：
（1）两个质数一定是互质数。例如，2与7、13与19。
（2）一个质数如果不能整除另一个合数，这两个数为互质数。例如，3与10、5与26。
（3）1不是质数也不是合数，它和任何一个自然数在一起都是互质数。如1和9908。
（4）相邻的两个自然数是互质数。如15与16。
（5）相邻的两个奇数是互质数。如49与51。
（6）大数是质数的两个数是互质数。如97与88。
（7）小数是质数，大数不是小数的倍数的两个数是互质数。如7和16。
（8）两个数都是合数（二数差又较大），小数所有的质因数，都不是大数的约数，这两个数是互质数。如357与715，357=3×7×17，而3、7和17都不是715的约数，这两个数为互质数。

3.欧拉函数
给定一个正整数n，计算在小于等于n的正整数之中，有多少个数与n构成互质关系的算法。
第一种情况：
如果n=1，则欧拉函数值为1，因为1与任何数都构成互质关系。
第二种情况：
如果n是质数，则欧拉函数的值为n-1,因为质数与小于它的每一个数构成互质关系。
第三种情况：
如果n是质数的某一个次方，即n=p^{k(p为质数，k为大于等于1的整数)，则函数值=p}k-p^（k-1）。
第四种情况：
n可以分解成两个互质的整数之积，n=p1p2
积的欧拉函数等于各个因子的欧拉函数之积。
例：56=78，7的欧拉函数是6，8的欧拉函数是4，所以56的欧拉函数是24.
第五种情况：
任意一个大于1的正整数，都可以写成一系列质数的积。

欧拉定理：如果两个正整数互质，则n的欧拉函数可以使得下面的等式成立，
例如3和7互质，7的欧拉函数是6，所以3的6次方减去1可以被7整除。

4.模反元素（不止一个），也叫乘法逆元。
如果两个正整数互质，那么一定可以找到整数b，使得ab-1被n整除，或者说ab被n除的余数是1，b就是a的模反元素。

5.模指数运算
模运算是整数运算，有一个整数m，以n为模做模运算，即m mod n。让m去被n整除，只取所得的余数作为结果，就叫做模运算。例如，10 mod 3=1；26 mod 6=2；28 mod 2 =0等等。模指数运算就是先做指数运算，取其结果再做模运算。如53 mod 7=125 mod 7=6。

三、算法设计
（一）需求分析
加密学号20031211537，通过计算发现这个数字的二进制数有36位。如果整体进行加密需要一个大于明文的N,所以N选择64位的无符号整数类型。这意味着P,Q也需要选取的比较大，然后P*Q才会产生一个比较大的N，因此P，Q也选为64位的无符号整数类型。然后将生成一个较大的公钥和私钥，这还不是最可怕的，最可怕的是将在这个基础上对明文进行加密，和对密文的解密。加密和解密将进行幂运算，对大整数的高次幂求解，首先计算机的内存不支持，其次计算机的处理能力也达不到。

要实现SRA算法，考虑解决的问题包括：
1.一次加密明文的长度，对超过加密长度的明文，需要实现切割功能。
2.设计求得大质数的算法，可以求得两个16位的二进制大质数。
3.自动生成公钥和私钥，确定公钥为65537，私钥通过改进的算法求得。
4.应该简化求幂运算的过程，对求幂运算的算法进行优化。
5.对应过程解密，还原明文。

（二）密钥生成
1.质数p,q的生成，确定加密明文长度euler。

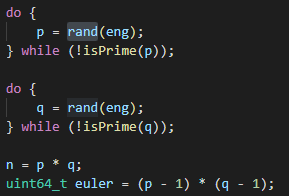
限定随机数的范围：0x8000,0xffff
随机的去取数，判断是否是符合要求的质数，如果是就退出循环。为方便后续的计算，我们取得的质数都是16位二进制的整数。
2.用欧几里得算法求两数最大公约数
欧几里得算法求两数最大公约数，又叫辗转相除法。
以1997和615为例，用欧几里得算法求解如下：
![在这里插入图片描述](https://img-blog.csdnimg.cn/20210620204528797.png

当被加的数为0时，可以得出，1997和615的最大公约数为1。
以上做法的依据是以下定理：
两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。
因此欧几里得算法的实现代码如下：

3.乘法逆元
扩展欧几里得：已知整数a,b，扩展欧几里得算法可以在求得a,b的最大公约数的同时，能找到整数x,y（其中一个很可能是负数），使它们满足贝祖等式，ax+by=gcd(a,b)。
因此可以将求乘法逆元转换为求扩展的欧几里得。

 在求得欧几里得的过程中，求得私钥。

（三）加密明文
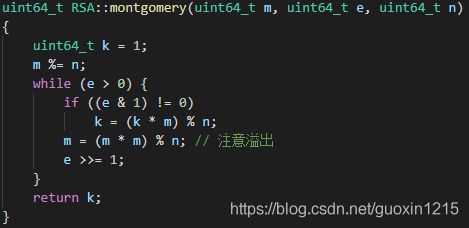
采用蒙哥马利大整数模幂运算法，快速计算出（m^e）%n的值

将输入明文字符转化为ASCII码，将四个字符方到一组进行加密。
一组表示为32位的无符号整型数据。

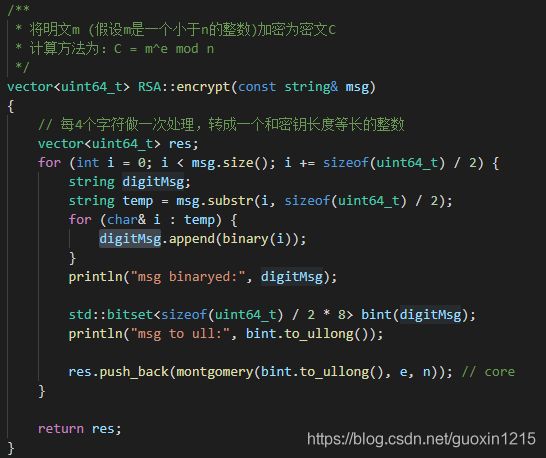
（四）解密密文

四、结果与总结
设计的算法基本实现RSA算法的加解密功能，可以加密数字，字符，汉字。
在设计算法的过程中，学到很多数学的知识，比如欧拉函数，互质，乘法逆元，欧几里得算法，蒙哥马利算法等。其次在实现算法的过程中，除了考虑算法的功能实现，还考虑了计算机的硬件存储，数据运算能力，编程语言的结构组织等。在算法实现过程中也踩到一些坑，比如贝祖等式中可能产生负数，这一点在最开始没有考虑，导致类型转换出了问题。另外在和同学的交流中，发现私钥的产生过程应该还可以优化，另外就是对模幂运算的进一步优化。总之纸上得来终觉浅，觉知此事要躬行!

五、备注
参考资料：
1.https://blog.csdn.net/zgzczzw/article/details/52712980
2.https://www.cnblogs.com/dupengcheng/p/5487362.htm
3.算法的代码gitee仓库地址：[email protected]:HolySoul/kronos.git
4.代码目录：kronos\kronos\CPlusPlusKingdom\ClassicCode\RSA\