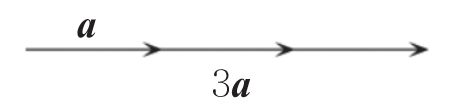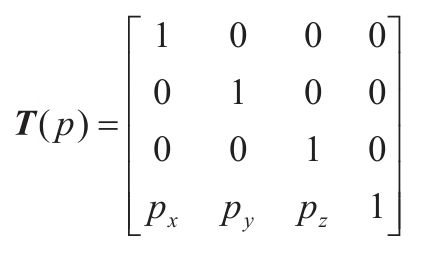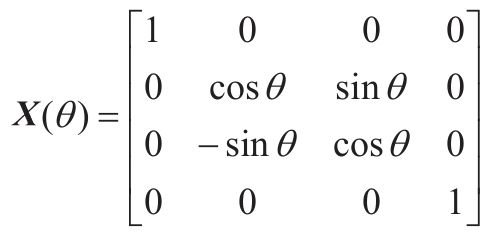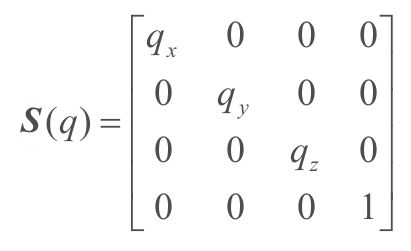【Unity3D】游戏开发数学基础
内容摘取总结自《Unity3D脚本编程与游戏开发》(马遥,沈琰)第四章——游戏开发数学基础
搬运自我的博客:浮生如梦 岁月如歌
文章目录
-
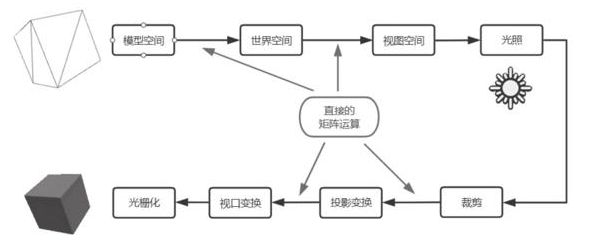
- 三维渲染流程示意图
- 坐标系
- 向量
- 矩阵
- 四元数
- 实例:第一人称视角的角色控制器
三维渲染流程示意图
坐标系
-
世界坐标系
全局坐标系是场景内所有物体和方向的基准,也称世界坐标系。在全局坐标系中的原点(0, 0, 0)是所有物体位置的基准,且全局坐标系指定了统一的x轴、y轴和z轴的朝向。
在Unity场景中,新建一个物体,坐标为(1, 2, 3)。那么它在x轴方向离原点1米,y轴方向离原点2米,z轴方向离原点3米。对于没有父物体的物体(场景中的第一级物体),Inspector窗口中显示的就是该物体在世界坐标系的位置、旋转和缩放比例。
-
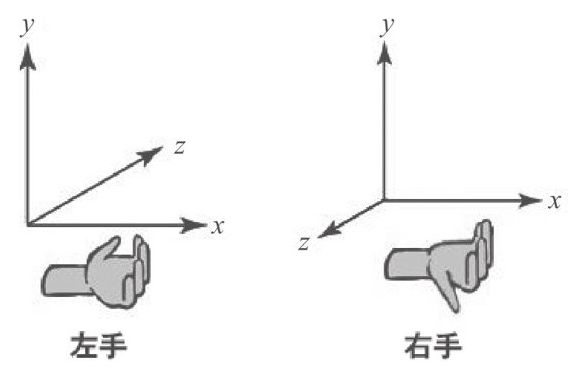
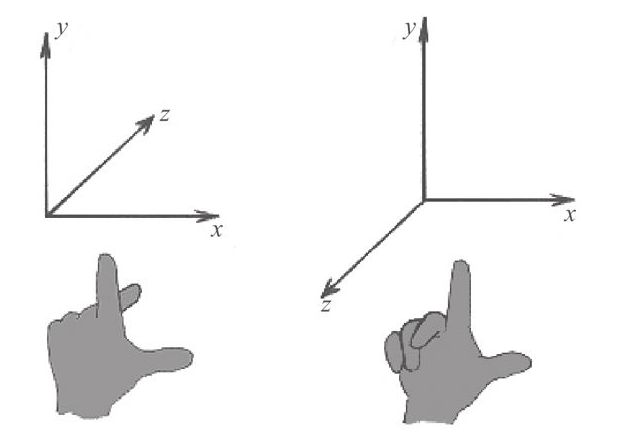
左手坐标系与右手坐标系
个人记忆:食指x轴,大拇指z轴,中指y轴
Unity采用左手坐标系,x轴、y轴和z轴分别默认为右、上、前。
-
熟记Unity坐标系顺序
熟悉并记住Unity中坐标轴和朝向的对应关系,可以极大提高场景编辑和编写代码的效率。
右,x轴;上,y轴;前,z轴。
x轴对应:右,(1, 0, 0),红色,Vector3.right。
y轴对应:上,(0, 1, 0),绿色,Vector3.up。
z轴对应:前,(0, 0, 1),蓝色,Vector3.forward。
-
局部坐标系
每个物体都有它的局部坐标系,局部坐标系会随着物体进行移动、旋转或缩放,局部坐标系也称本地坐标系。以身高1.8米的人体为例,如果设人的脚底为局部坐标系的原点,那么人的腰部大约位于(0, 1.2, 0)的位置,头顶位于约(0, 1.8, 0)的位置。
图所示的下方物体是父物体,它的坐标为(1, 2, 0),上方物体是子物体,相对父物体的局部坐标是(3 ,2 ,0 )。在编辑器中分别选择两个物体,看到的坐标正是(1, 2, 0)和(3, 2, 0)。也就是说,编辑器面板上的坐标数值,全都可以理解为局部坐标系的数值。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7hFJDOpS-1650014382216)(https://p.rayhirox.com/i/2022/04/15/qtzu5o.png)]
但是前文提到,对于场景中的第一级物体(没有父物体的物体),编辑器面板显示的是世界坐标系的数值,这里是不是存在矛盾呢?其实并没有问题,因为第一级物体的父节点就是场景本身,而场景的坐标系与世界坐标系是一致的。
图所示的子物体相对父物体的坐标为(3, 2, 0),而子物体的世界坐标是(4, 4, 0),即(3+1, 2+2, 0+0)。脚本中获取物体的世界坐标和相对父物体的坐标的方法如下。
using UnityEngine;
public class PositionTest : MonoBehaviour
{
void Start()
{
// 当前物体的世界坐标系位置
Vector3 worldPos = transform.position;
Debug.Log("World Pos:" + worldPos);
// 当前物体相对父物体的位置
Vector3 localPos = transform.localPosition;
Debug.Log("Local Pos:" + localPos);
}
}
- 局部坐标系下的朝向和缩放比例
// 旋转
Quaternion worldRotation = transform.rotation;
Quaternion localRotation = transform.localRotation;
// 在父物体局部坐标系下的缩放。无法直接获得世界坐标系的缩放
Vector3 localScale = transform.localScale;
// 物体向着世界上方移动一米
transform.position += Vector3.up;
// 物体向自身的上方移动一米
transform.Translate(Vector3.up);
// 上面一句代码等价于下面这句
transform.position += transform.up;
// 错误的写法会导致计算结果意义不明
transform.Translate(transform.up); // !!! 错误的写法
- 屏幕坐标系
// 鼠标指针位置是屏幕坐标系
Vector2 mousePos = Input.mousePosition;
Debug.Log("鼠标指针在屏幕上的位置:" + mousePos);
// 将鼠标指针位置转化为视图坐标系时,需要利用摄像机计算
Vector3 viewPoint = Camera.main.ScreenToViewportPoint(Input.mousePosition);
Debug.Log("鼠标指针位置的视图坐标为:" + viewPoint);
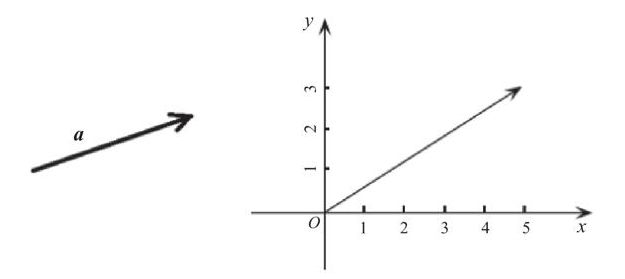
向量
- 向量加法
(x1,y1,z1)+(x2,y2,z2)=(x1+x2,y1+y2,z1+z2)
- 向量减法
(x1,y1,z1)-(x2,y2,z2)=(x1-x2,y1-y2,z1-z2)
- 向量的数乘
k(x,y,z)=(kx,ky,kz)
Vector3 a=new Vector3(2,1,0);
Vector3 na=a/a.magnitude; //a.magnitude就是a的长度,术语叫作“a的模”
//以上写法等价于:
Vector3 na2=a.normalized;
//还等价于:
Vector3 na3=Vector3.Normalized(a);//向量的标准化
//还等价于:
Vector3 na4=(1/a.magnitude)*a;
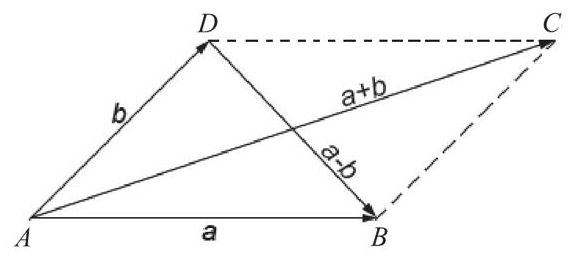
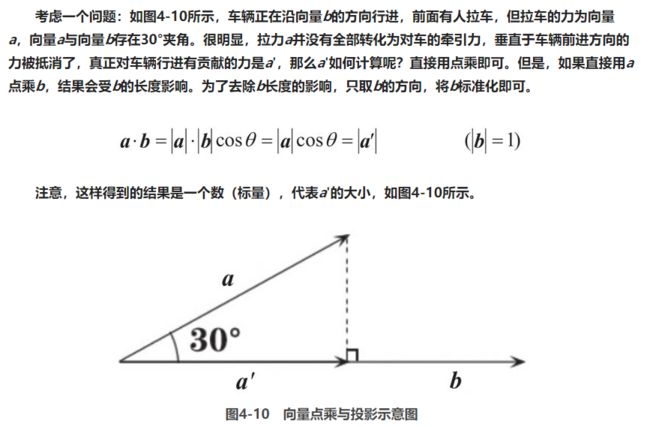
- 向量的点积
(a·b=|a|·|b|cosθ)
(x1,y1,z1)·(x2,y2,z2)=x1·x2+y1·y2+z1·z2
以及投影:
Vector3 a=new Vector3(2,1,0);
Vector3 b=new Vector3(3,0,0);
Vector3 dir_b=b.nomalized; //dir_b是标准化的向量b
float pa=Vector3.dot(a,dir_b); //pa即是向量a在向量b方向的投影长度
- 向量的叉积
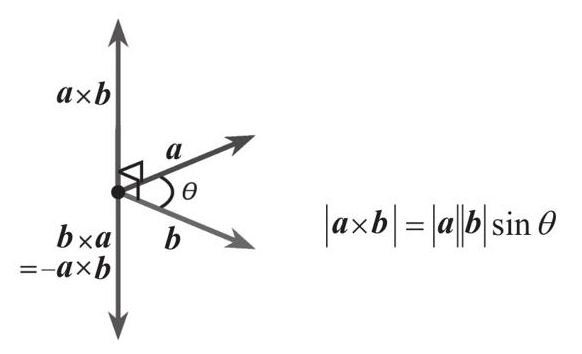
手掌沿第1个向量放平,向第2个向量握拳,拇指的指向即叉积方向。
当向量a与向量b共线(同向或反向)时,叉积为0向量。
Vector3 a=new Vector3(2,1,1); //a和b是某个平面上的任意两个向量
Vector3 b=new Vector3(3,0,2);
Vector3 n=Vector3.Cross(a,b); //n是该平面的法线
n=n.nor m alized; //将n标准化
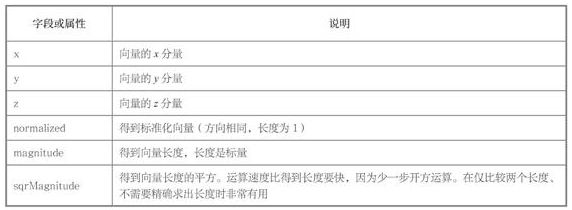
- Vector3结构体
Vector3的属性
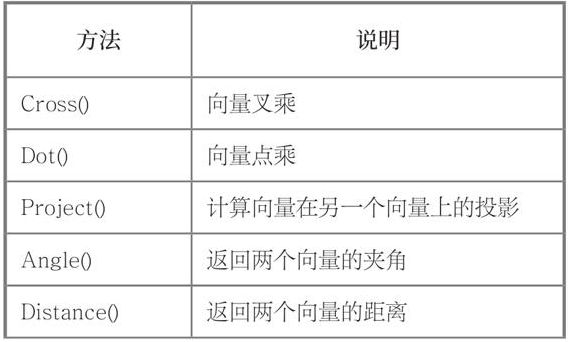
Vector3的方法
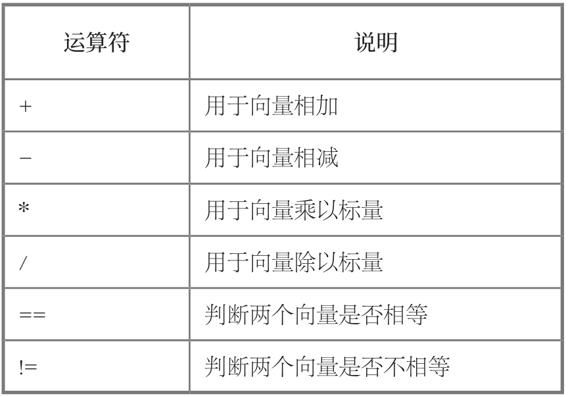
Vector3的运算符
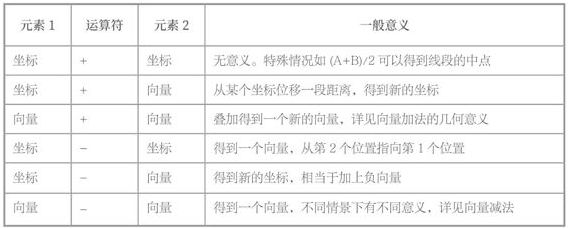
- 位置与向量的关联
//这是当前物体的A坐标
Vector3 p1=transform.position;
//这是物体B的坐标
Vector3 p2=gameObjectB.transform.position;
//这是从当前物体A到B的向量
Vector3 diff=p2-p1;
//获得了一个新的坐标C,位于比B远离当前物体A一倍的位置
Vector3 p3=p2+diff;
//从物体C的位置出发,发生从A到B的位移,得到新的坐标
Vector3 p3=gameObjectC.transform.position+diff;
//调整向量的长度为一半
Vector3 diffHalf=diff*0.5f;
- 向量坐标系的转换
可以使用transform.TransformPoint()方法将局部坐标转换为世界坐标,也可以使用transform.InverseTransformPoint()方法将世界坐标转换为局部坐标。transform.TransformDirection()和transform.InverseTransformDirection()方法则用于向量的全局坐标系和局部坐标系之间的转换。两者的差异在于TransformPoint()是转换坐标专用的,TransformDirection()是转换向量专用的。
using UnityEngine;
public class CoordinateLocal:MonoBehaviour{
void Update(){
transform.Translate(Vector3.forward*Time.deltaTime);
}
}//沿自身的z轴
using UnityEngine;
public class CoordinateWorld:MonoBehaviour{
void Update(){
Vector3 v=transform.InverseTransformDirection(Vector3.forward);
transform.Translate(v*Time.deltaTime);
}
}//沿世界坐标系的z轴
矩阵
- 平移矩阵
向量v乘以T(p),相当于让向量v的x、y、z分量分别变化px、py、pz。
- 旋转矩阵
此矩阵可以让向量沿着x轴旋转θ角。
- 缩放矩阵
缩放矩阵可以对向量的各个分量进行缩放,向量v与S(q)相乘后,v的3个分量分别缩放qx、qy、qz倍。
- 齐次坐标
在3D数学中,齐次坐标就是将原本的三维向量(x, y, z)用四维向量(x, y, z, w)来表示。
引入齐次坐标有如下目的。
更好地区分坐标点和向量。在三维空间中,(x, y, z)既可以表示一个点,也可以表示一个向量。如果采用齐次坐标,则可以使用(x, y, z, 1)代表坐标点,而用(x, y, z, 0)代表向量。在进行一些错误操作时,例如将两个坐标点相加,会立即得到一个错误的结果,避免引起混乱。
四元数
在场景窗口中旋转物体是一项基本操作。可以用旋转工具改变物体角度,也可以在Inspector窗口中改变物体的X、Y、Z值(欧拉角)来改变物体角度。用欧拉角表示角度和旋转,简单又直观。但一般人想不到,物体在三维空间中的旋转并不是一个简单问题,用3个角度表示是远远不够的。
- 万向节锁定
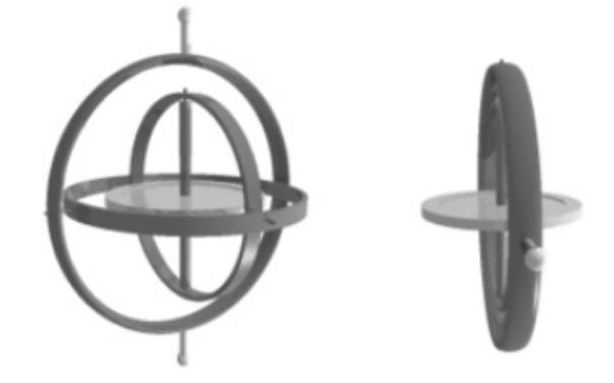
要说明三维物体旋转的复杂性,从“万向节锁定”这一问题入手最有说服力。
虽然可以调整欧拉角到任意角度,但欧拉角的3个轴并不是独立的,x轴、y轴和z轴之间存在嵌套结构,如图4-15所示,这种嵌套结构被称为“万向节”,意思是可以转到任意角度的关节。
当中层轴旋转时,会带动内层的轴跟着旋转。通常三维软件的欧拉角,从外层到内层是按照y轴→x轴→z轴的顺序,也就是说沿x轴的旋转会影响z轴。
Unity引擎内部并没有万向节锁定问题
值得说明的是,Unity内部是用四元数表示物体的旋转,这里并不会真的遇到锁定问题,只是在编辑器界面上模拟了万向节锁定的效果。如果用旋转工具在场景里直接旋转物体,就跳过了编辑窗口的限制,物体仍然可以自由旋转。
- 四元数的概念
四元数包含一个标量分量和一个三维向量分量,四元数Q可以记作
Q=[w,(x,y,z)]
在3D数学中使用单位四元数表示旋转,下面给出四元数的公式定义。对于三维空间中旋转轴为n,旋转角度为a的旋转,如果用四元数表示,则4个分量分别为
w=cos(α/2)
x=sin(α/2 )cos (βx)
y=sin(α/2 )cos (βy)
z=sin( α/2 )cos (βz)
用四元数表示旋转一点也不直观,4个分量w、x、y和z与绕各轴的旋转角度并没有直接的对应关系。在实际游戏开发中不要试图获取和修改某一个分量,应当只做整体处理。
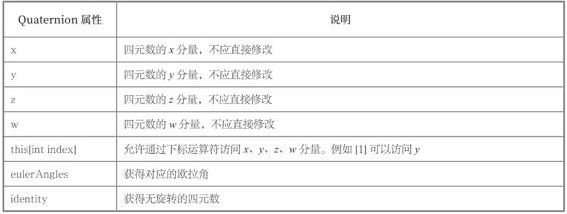
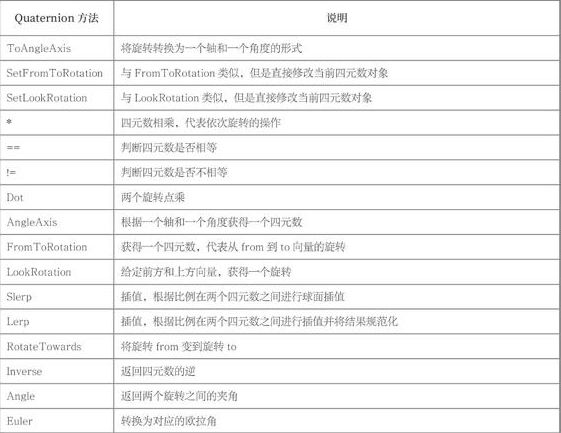
- Quaternion结构体
四元数的属性
四元数的方法和运算符
- 理解和运用四元数
“旋转”有点像前文提到的“向量”,指的是一个旋转的变化量。例如“右转90°”就是一个旋转,如果面朝南,右转90°就是朝西;如果面朝东,右转90°就是朝南。将位置、向量与朝向、旋转类比,可以形成清晰的概念。
前文提到,位置和向量都是用Vector3表示。不出意料,朝向和旋转都是用四元数(Quaternion)表示。理解了Vector3加法的意义,就可以类比出四元数的旋转操作,只是加法变成了乘法。
四元数相乘不满足交换律
注意四元数乘以向量时,必须四元数在前,向量在后。不存在“向量四元数”的操作,代码中写“向量四元数”会报错。
using UnityEngine;
public class QuatTest : MonoBehaviour
{
void Update()
{
float v = Input.GetAxis("Vertical");
float h = Input.GetAxis("Horizontal");
// 将横向输入转化为左右旋转,将纵向输入转化为俯仰旋转,得到一个很小的旋转四元数
Quaternion smallRotate = Quaternion.Euler(v, h, 0);
// 将这个小的旋转叠加到当前旋转位置上
if (Input.GetButton("Fire1"))
{
// 按住鼠标左键或Ctrl键时,沿世界坐标轴旋转
transform.rotation = smallRotate * transform.rotation;
}
else
{
// 不按鼠标左键和Ctrl键时,沿局部坐标轴旋转
transform.rotation = transform.rotation * smallRotate;
}
}
}
- 四元数的插值
四元数有两种插值函数,四元数除了有Slerp方法,也有Lerp方法。由于Lerp方法不是严格的球面插值,因此一般情况下使用Slerp方法。
static Quaternion Slerp(Quaternion a, Quaternion b, float t);
/ 前方
Quaternion q = Quaternion.identity; // identity相当于Eular(0, 0, 0),不旋转
// 改变物体的朝向,取当前朝向与正前方之间10%的位置
transform.rotation = Quaternion.Slerp(transform.rotation, q, 0.1f);
- 朝向与向量
using UnityEngine;
public class MouseRotation : MonoBehaviour
{
void Update()
{
Ray ray = Camera.main.ScreenPointToRay(Input.mousePosition);
RaycastHit hit;
if (Physics.Raycast(ray, out hit))
{
transform.forward = hit.point - transform.position;
}
}
}
if (Physics.Raycast(ray, out hit))
{
// 防止角色低头的代码
Vector3 v = hit.point - transform.position;
v.y = transform.y;
transform.forward = v;
}
//向量转化为四元数(朝向)的方法定义如下
Quaternion Quaternion.LookRotation(Vector3 forward);
Quaternion Quaternion.LookRotation(Vector3 forward, Vector3 up);
实例:第一人称视角的角色控制器
using UnityEngine;
public class FPSCharacter : MonoBehaviour
{
public float speed = 5f;
void Start()
{
// 隐藏鼠标指针
Cursor.visible = false;
// 锁定鼠标指针到屏幕中央
Cursor.lockState = CursorLockMode.Locked;
}
void Update()
{
Move();
MouseLook();
}
void Move()
{
float x = Input.GetAxis("Horizontal"); // 输入左右
float z = Input.GetAxis("Vertical"); // 输入前后
// 方向永远平行地面,角色不能走到天上去
// 获得角色前方向量,将Y轴分量设为0
Vector3 fwd = transform.forward;
Vector3 f = new Vector3(fwd.x, 0, fwd.z).normalized;
// 角色的右方向量与右方向的移动直接对应,与抬头无关,可以直接用
Vector3 r = transform.right;
// 用f和r作向量的基,组合成移动向量
Vector3 move = f * z + r * x;
// 直接改变玩家位置
transform.position += move * speed * Time.deltaTime;
}
void MouseLook()
{
float mx = Input.GetAxis("Mouse X");
float my = -Input.GetAxis("Mouse Y");
Quaternion qx = Quaternion.Euler(0, mx, 0);
Quaternion qy = Quaternion.Euler(my, 0, 0);
transform.rotation = qx * transform.rotation;
transform.rotation = transform.rotation * qy;
// angle 是俯仰角度
float angle = transform.eulerAngles.x;
// 使用欧拉角时,经常出现-1°和359°混乱等情况,下面对这些情况加以处理
if (angle > 180) { angle -= 360; }
if (angle < -180) { angle += 360; }
// 限制抬头、低头角度
if (angle > 80)
{
transform.eulerAngles = new Vector3(80, transform.eulerAngles.y, 0);
}
if (angle < -80)
{
transform.eulerAngles = new Vector3(-80, transform.eulerAngles.y, 0);
}
}
}
Rayhirox于2022-04-08使用Notion整理完毕