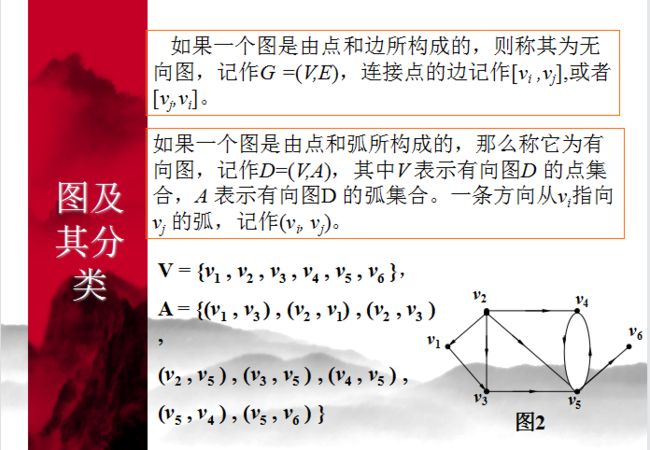
1 概述
1.1 贪心算法
贪心算法总是作出在当前看来最好的选择。也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。当然,希望贪心算法得到的最终结果也是整体最优的。虽然贪心算法不能对所有问题都得到整体最优解,但对许多问题它能产生整体最优解。如单源最短路经问题,最小生成树问题等。在一些情况下,即使贪心算法不能得到整体最优解,其最终结果却是最优解的很好近似。
基本思路:从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的地求得更好的解。当达到算法中的某一步不能再继续前进时,算法停止。
该算法存在问题:
- (1)不能保证求得的最后解是最佳的;
- (2)不能用来求最大或最小解问题;
- (3)只能求满足某些约束条件的可行解的范围。
实现该算法的伪代码:
从问题的某一初始解出发;
while 能朝给定总目标前进一步 do
求出可行解的一个解元素由所有解元素组合成问题的一个可行解;
1.2 图论及求解最短距离
1.2.1 方法选择
- (1)需要求解任意两个节点之间的最短距离,使用 Floyd 算法;
- (2)只要求解单源最短路径问题,有负权边时使用 Bellman-Ford 算法,没有负权边时使用 Dijkstra 算法;
- (3)A*算法找到的是相对最优路径,适合大规模、实时性高的问题。
本节我们只讨论Dijkstra 算法。
1.2.2 狄克斯屈拉(Dijkstra)算法
适用于wij≥0,给出了从vs到任意一个点vj的最短路。
Dijkstra算法是在1959年提出来的。目前公认,在所有的权wij ≥0时,这个算法是寻求最短路问题最好的算法。并且,这个算法实际
上也给出了寻求从一个始定点vs到任意一个点vj的最短路。
2 案例1——贪心算法实现
2.1 旅行商问题(TSP)
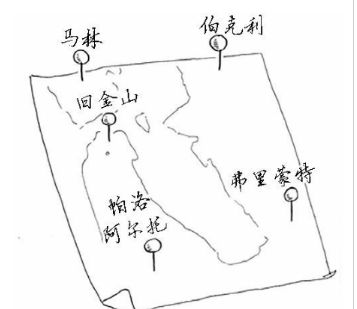
旅行商问题(TravelingSalesmanProblem,TSP)一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要遍历所有城市一次且只能一次,回到出发地。应如何选择行进路线,以使总的行程最短。
旅行商问题(TSP)即给定一组城市以及每对城市之间的距离,需要找到一条最短的路线,该路线只对每个城市进行一次访问并返回起点。
这里注意汉密尔顿活路(Hamiltonian Cycle)和TSP之间的区别。汉密尔顿回路问题是要找出是否存在一次游览每个城市一次的路线。在TSP问题中,我们是已知存在汉密尔顿回路(因为该图是完整的),并且实际上,存在许多此类回路,TSP问题在于找到最小权重的汉密尔顿回路。
目前解决TSP问题的方法有许多种,比如:贪心算法、动态规划算法、分支限界法;也有智能算法。本文先介绍贪心算法:
2.2 案例
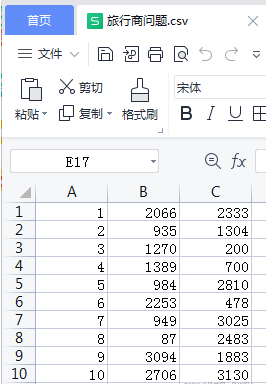
数据 如下图,第一列城市名。第二列坐标x,第三列坐标y:
贪心算法思路:随便选择出发城市,然后每次选择要去的下一个城市时,都选择还没去的最近的城市。
2.3 Python实现
#========第一步:导入相关库==================
import pandas as pd
import numpy as np
import math
import time
#======第二步:读取数据=================
dataframe = pd.read_csv("旅行商问题.csv", sep=",", header=None)
v = dataframe.iloc[:, 1:3] #去除第一列12345678910,只保留x,y
print('读取数据:----------------------------')
print(v)
#=======第三步:计算城市之间的距离========
train_v= np.array(v)
train_d=train_v
dist = np.zeros((train_v.shape[0],train_d.shape[0])) #初始化距离 为10*10的全0矩阵
print(dist.shape) #(10,10)
#==计算距离矩阵===
for i in range(train_v.shape[0]):
for j in range(train_d.shape[0]):
dist[i,j] = math.sqrt(np.sum((train_v[i,:]-train_d[j,:])**2))
print('距离矩阵:----------------------------------')
print(dist)
#==========第四步:计算距离和路径==============
"""
s:已经遍历过的城市
dist:城市间距离矩阵
sumpath:目前的最小路径总长度
Dtemp:当前最小距离
flag:访问标记
"""
i=1
n=train_v.shape[0]#城市个数
j=0
sumpath=0#目前的最小路径总长度
s=[]#已经遍历过的城市
s.append(0)#从城市0开始
start = time.perf_counter() #time.clock()
while True:
k=1#从1开始,因为人在城市0,所以我们设定先从城市1开始选择
Detemp=float('inf')#当前最小距离
while True:
flag=0#访问标记,否0
if k in s:#是否访问,如果访问过,flag设为1
flag = 1
if (flag==0) and (dist[k][s[i-1]] < Detemp):#如果未访问过,并且距离小于最小距离
j = k;
Detemp=dist[k][s[i - 1]]; #当前两座城市相邻距离
k+=1#遍历下一城市
if k>=n:
break;
s.append(j)
i+=1;
sumpath+=Detemp
if i>=n:
break;
sumpath+=dist[0][j]#加上dist[0][j] 表示最后又回到起点
end = time.perf_counter() #time.clock()
print("距离:")
print(sumpath)
print('*--------------*')
print('路径:')
for m in range(n):
print("%s-> "%(s[m]),end='')
print()
print("程序的运行时间是:%s"%(end-start))
代码解析:数字k表示当前我们选择前往下一个城市时,我们需要计算所有未访问过的城市和当前城市距离。
数字i 用于控制访问过的城市,我们需要到达每一个城市。
代码中有两个while
里面那个while表示选择下一城市时,需要遍历所有未访问过的城市,然后选择距离当前城市最近的城市,赋值给j
外面while,表示我们的每一步,我们需要去每个城市。
2.4 结果
读取数据:
1 2
0 2066 2333
1 935 1304
2 1270 200
3 1389 700
4 984 2810
5 2253 478
6 949 3025
7 87 2483
8 3094 1883
9 2706 3130
(10, 10)
距离矩阵:----------------------------------
[[ 0. 1529.05264788 2276.68728639 1767.77204413 1182.47748393
1864.40178073 1313.98363765 1984.67654795 1122.17823896 1022.15898959]
[1529.05264788 0. 1153.70750193 755.6004235 1506.7969339
1555.44205935 1721.0569427 1452.28957168 2235.29013777 2543.76040538]
[2276.68728639 1153.70750193 0. 513.96595218 2625.6229737
1021.55420806 2843.17885473 2571.29889356 2481.82694804 3262.97349055]
[1767.77204413 755.6004235 513.96595218 0. 2148.51693035
892.06502005 2366.26815894 2207.7801068 2075.21420581 2763.94446399]
[1182.47748393 1506.7969339 2625.6229737 2148.51693035 0.
2654.91713618 217.83020911 954.74499213 2304.65377009 1751.48051659]
[1864.40178073 1555.44205935 1021.55420806 892.06502005 2654.91713618
0. 2861.40262808 2951.53875123 1637.46938903 2690.41130685]
[1313.98363765 1721.0569427 2843.17885473 2366.26815894 217.83020911
2861.40262808 0. 1018.23769327 2430.05946429 1760.13465394]
[1984.67654795 1452.28957168 2571.29889356 2207.7801068 954.74499213
2951.53875123 1018.23769327 0. 3066.2760802 2697.7342345 ]
[1122.17823896 2235.29013777 2481.82694804 2075.21420581 2304.65377009
1637.46938903 2430.05946429 3066.2760802 0. 1305.9682232 ]
[1022.15898959 2543.76040538 3262.97349055 2763.94446399 1751.48051659
2690.41130685 1760.13465394 2697.7342345 1305.9682232 0. ]]
距离:
10464.183486532447
*--------------*
路径:
0-> 9-> 8-> 5-> 3-> 2-> 1-> 7-> 4-> 6->
程序的运行时间是:0.0002605780000024538
Process finished with exit code 0
3 案例2——图论及最短距离
3.1 知识点
3.2 networkx绘图
3.2.1 创建图
networkx有四种图 Graph 、DiGraph、MultiGraph、MultiDiGraph,分别为无多重边无向图、无多重边有向图、有多重边无向图、有多重边有向图。
#==========创建图================ import networkx as nx # 导入 NetworkX 工具包 G1 = nx.Graph() # 创建:空的 无向图 G2 = nx.DiGraph() #创建:空的 有向图 G3 = nx.MultiGraph() #创建:空的 多图 G4 = nx.MultiDiGraph() #创建:空的 有向多图
3.2.2 定点的添加、删除和查看
#================顶点的添加、删除和查看=============
#======顶点(node)的操作=====
#==向图中添加顶点==
G1.add_node(1) # 向 G1 添加顶点 1
G1.add_node(1, name='n1', weight=1.0) # 添加顶点 1,定义 name, weight 属性
G1.add_node(2, date='May-16') # 添加顶点 2,定义 time 属性
G1.add_nodes_from([3, 0, 6], dist=1) # 添加多个顶点,并定义属性
G1.add_nodes_from(range(10, 15)) # 向图 G1 添加顶点 10~14
#==查看顶点和顶点属性==
print(G1.nodes()) # 查看顶点列表
# [1, 2, 3, 0, 6, 10, 11, 12, 13, 14]
print(G1._node) # 查看顶点属性
# {1: {'name': 'n1', 'weight': 1.0}, 2: {'date': 'May-16'}, 3: {'dist': 1}, 0: {'dist': 1}, 6: {'dist': 1}, 10: {}, 11: {}, 12: {}, 13: {}, 14: {}}
#==从图中删除顶点==
G1.remove_node(1) # 删除顶点
G1.remove_nodes_from([1, 11, 13, 14]) # 通过顶点标签的 list 删除多个顶点
print(G1.nodes()) # 查看顶点
# [2, 3, 0, 6, 10, 12] # 顶点列表
3.2.3 边的添加、删除和查看
#====================边的添加、删除和查看================
#========边(edge)的操作========
#==向图中添加边==
G1.add_edge(1,5) # 向 G1 添加边,并自动添加图中没有的顶点
G1.add_edge(0,10, weight=2.7) # 向 G1 添加边,并设置边的属性
G1.add_edges_from([(1,2,{'weight':0}), (2,3,{'color':'blue'})]) # 向图中添加边,并设置#==属性==
G1.add_edges_from([(3,6),(1,2),(6,7),(5,10),(0,1)]) # 向图中添加多条边
G1.add_weighted_edges_from([(1,2,3.6),[6,12,0.5]]) # 向图中添加多条赋权边: (node1,node2,weight)
print(G1.nodes()) # 查看顶点
# [2, 3, 0, 6, 10, 12, 1, 5, 7] # 自动添加了图中没有的顶点
#==从图中删除边==
G1.remove_edge(0,1) # 从图中删除边 0-1
G1.remove_edges_from([(2,3),(1,5),(6,7)]) # 从图中删除多条边
#==查看边和边的属性==
print(G1.edges) # 查看所有的边
[(2, 1), (3, 6), (0, 10), (6, 12), (10, 5)]
print(G1.get_edge_data(1,2)) # 查看指定边的属性
# {'weight': 3.6}
print(G1[1][2]) # 查看指定边的属性
# {'weight': 3.6}
print(G1.edges(data=True)) # 查看所有边的属性
# [(2, 1, {'weight': 3.6}), (3, 6, {}), (0, 10, {'weight': 2.7}), (6, 12, {'weight': 0.5}), (10, 5, {})]
3.3 案例
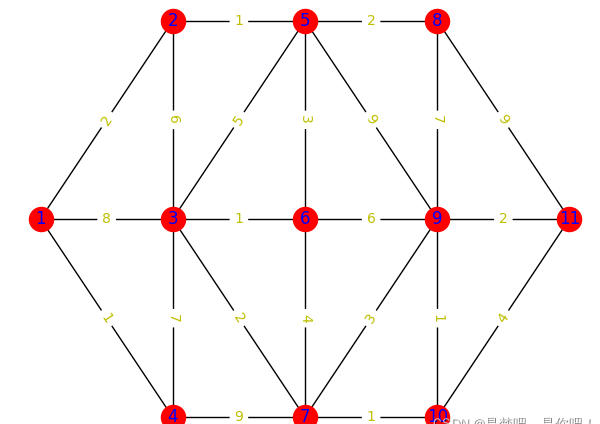
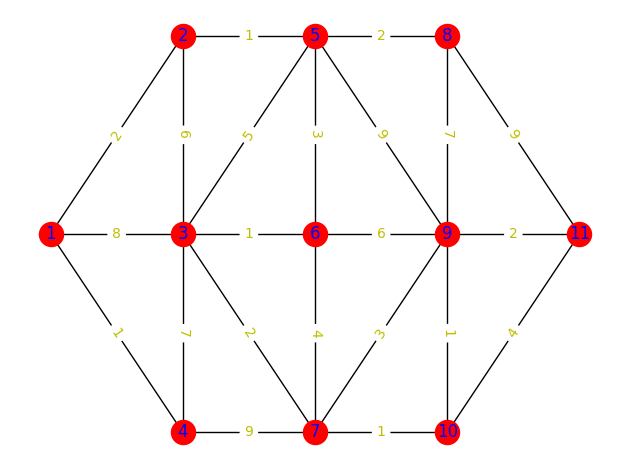
例题 1:已知如图的有权无向图,求顶点 v1 到 顶点 v11 的最短路径。
3.4 Python实现
#========导入相关包=========================
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx # 导入 NetworkX 工具包
#======问题:无向图的最短路问题===============
G1 = nx.Graph() # 创建:空的 无向图
G1.add_weighted_edges_from([(1,2,2),(1,3,8),(1,4,1),
(2,3,6),(2,5,1),
(3,4,7),(3,5,5),(3,6,1),(3,7,2),
(4,7,9),
(5,6,3),(5,8,2),(5,9,9),
(6,7,4),(6,9,6),
(7,9,3),(7,10,1),
(8,9,7),(8,11,9),
(9,10,1),(9,11,2),
(10,11,4)]) # 向图中添加多条赋权边: (node1,node2,weight)
print('nx.info:',G1.nodes) # 返回图的基本信息,nx.info:返回图的基本信息
#=======两个指定顶点之间的最短加权路径===============
minWPath_v1_v11 = nx.dijkstra_path(G1, source=1, target=11) # 顶点 1 到 顶点 11 的最短加权路径
print("顶点 v1 到 顶点 v11 的最短加权路径: ", minWPath_v1_v11)
# 两个指定顶点之间的最短加权路径的长度
lMinWPath_v1_v11 = nx.dijkstra_path_length(G1, source=1, target=11) # 最短加权路径长度
print("顶点 v1 到 顶点 v11 的最短加权路径长度: ", lMinWPath_v1_v11)
pos = {1: (0,4), 2: (5,7), 3: (5,4), 4: (5,1), 5: (10,7), 6: (10,4), 7: (10,1),
8: (15,7), 9: (15,4), 10: (15,1), 11: (20,4)} # 指定顶点位置,以节点为键,位置为值的字典
labels = nx.get_edge_attributes(G1, 'weight') # 设置边的 labels 为 ‘weight'
nx.draw(G1, pos,node_color = 'r',with_labels=True, font_color='b') # 绘制无向图,pos 指的是布局
nx.draw_networkx_edge_labels(G1, pos, edge_labels=labels, font_color='y') # 显示边的权值
plt.show()
- 1、Python Network(二)绘图draw系列draw(),draw_networkx(),draw_networkx_nodes(),draw_networkx_edges()
- 2、用Python的networkx绘制精美网络图
3.5 结果
nx.info: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
顶点 v1 到 顶点 v11 的最短加权路径: [1, 2, 5, 6, 3, 7, 10, 9, 11]
顶点 v1 到 顶点 v11 的最短加权路径长度: 13
到此这篇关于运筹学-Python实现图论与最短距离的文章就介绍到这了,更多相关Python实现图论与最短距离内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!