JS中toFixed()方法四舍五入的精度问题详解

目录

• 踩的坑
• 填坑方法
• 什么样的坑？
• 总结

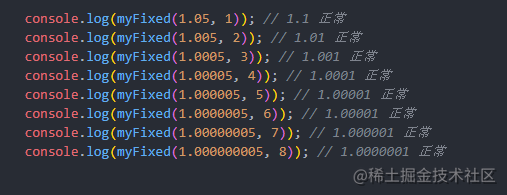
踩的坑

最近工作中，在计算一个商品的折扣价格，有时候总是出现价格会有一分钱的差异，涉及钱的问题都是比较敏感的，经过排查，最后发现竟然是 JS 原生的 toFixed 方法的问题。

好家伙，这都啥规律啊。。。(⊙o⊙)

填坑方法

先不着急去探究其中的问题，既然发现了问题，那就先把 Bug 修复了先，原生方法用不了，就自己写一个呗，还不是分分钟的事情，哈哈哈！

/**
 * 保留小数点几位数, 自动补零, 四舍五入
 * @param num: 数值
 * @param digit: 小数点后位数
 * @returns string
 */ 
function myFixed(num, digit) {
  if(Object.is(parseFloat(num), NaN)) {
    return console.log(`传入的值：${num}不是一个数字`);
  }
  num = parseFloat(num);
  return (Math.round((num + Number.EPSILON) * Math.pow(10, digit)) / Math.pow(10, digit)).toFixed(digit);
}

什么样的坑？

好了，既然 Bug 解决完了，下面我们就来探索一下 toFixed 其中的奥秘。

呃...首先，Em...百度一下吧，面向百度编程工程师，果然一查大把结果，看来是个经典问题了。

经过一番了解得知，原来是 toFixed 方法采用的四舍五入，并不是我们理解的字面上的四舍五入。而 toFixed 方法它是采用一种诡异的方法 "四舍六入五取偶" ，也叫银行家算法，这是什么个意思呢？

完整说法："四舍六入五考虑，五后非零就进一，五后为零看奇偶，五前为偶应舍去，五前为奇要进一"。

大概意思是：当舍去位的数值 ≤4 时舍去，当它 ≥6 时加上，可当它 =5 时，则根据 5 后面的数字来定；当 5 后有非零数字时，舍 5 入 1；当 5 后无有效数字时，需要再分两种情况：5 前为偶数，舍 5 不进；5 前为奇数，舍 5 入 1 。

根据这个规则，我在浏览器上又跑了一些测试，但却还是感觉不对。

// 五前是偶数，没有舍去？
console.log(1.00000065.toFixed(7)); // 1.0000007 错误
console.log(1.000000065.toFixed(8)); // 1.00000007 错误
// 五前是奇数，没有进一？
console.log(1.00000015.toFixed(7)); // 1.0000001 错误
console.log(1.000000015.toFixed(8)); // 1.00000001 错误

这到底为啥？真是让人摸不着头脑。。。（︶︿︶）

再经过一番探索，总算是有点收获了，下面就得来看看 ECMAScript 规范对该方法的定义了，有时候回归规范才是最靠谱的方式。

上图是关于整个 toFixed 方法的定义，不过是翻译后的版本，会有出入但差别不大，也可以点击上面的链接查看原文，我们主要关注图中红框部分，通过公式来计算舍去位数值。

我们下面两个来举个栗子，测试一下。

console.log(1.0000005.toFixed(6)); // 1.000001 正确
console.log(1.00000005.toFixed(7)); // 1.0000000 错误  

首先，根据红框的条件，x<10^21，1.0000005 与 1.00000005 都是小于 10^21 的，所以我们直接可以使用公式 n / 10^ - x 来玩耍。

我们先用 x=1.0000005 代入公式来看看情况：

// 假设n1
var n1 = 1000000;
var x = 1.0000005;
var f = 6;
console.log((n1 / Math.pow(10, f) - x)); // -5.00000000069889e-7

// 假设n2
var n2 = 1000001;
var x = 1.0000005;
var f = 6;
console.log((n2 / Math.pow(10, f) - x)); // 4.999999998478444e-7

由结果可知，当 n1=1000001 时，得到的结果取最接近 0 的值，故：

console.log(1.0000005.toFixed(6)); // 1.000001 正确

再来试试当 x=1.00000005 代入公式：

// 假设n1
var n1 = 10000000;
var x = 1.00000005;
var f = 7;
console.log((n1 / Math.pow(10,f) - x)); // -4.9999999918171056e-8

// 假设n2
var n2 = 10000001;
var x = 1.00000005;
var f = 7;
console.log((n2 / Math.pow(10,f) - x)); // 5.000000014021566e-8

由结果可知，当 n2=10000001 时，得到的结果取最接近 0 的值，故：

console.log(1.00000005.toFixed(7)); // 1.0000000 错误

哎...写到这里才发现给自己挖了一个大坑，干嘛要搞那么多零，自己都数晕圈了。。。

总的来说，上面例子就是教你如何通过规范定义的公式计算出结果而已，如果你看得懂规范，那么直接去代入也是没有问题的。

总结

到此这篇关于JS中toFixed()方法四舍五入精度问题的文章就介绍到这了,更多相关JS toFixed()四舍五入精度问题内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！