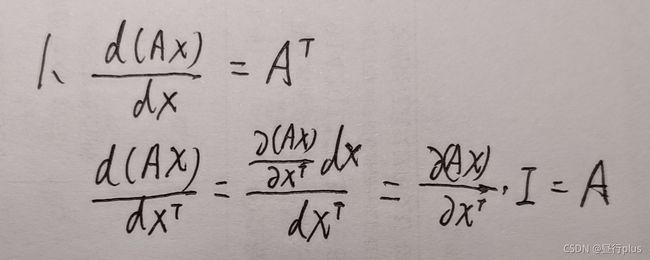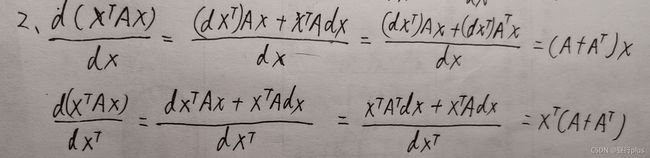视觉SLAM入门 -- 学习笔记 - Part4
2 图像去畸变
本次作业,你将尝试如何对一张图像去畸变,得到畸变前的图像。
图1: 测试图像
图1 是本次习题的测试图像(code/test.png),来自EuRoC 数据集。可以明显看到实际的柱子、箱子的直线边缘在图像中被扭曲成了曲线。这就是由相机畸变造成的。根据我们在课上的介绍,畸变前后的坐标变换为:
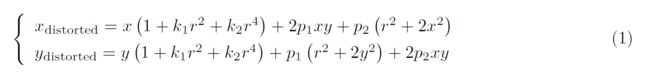
其中x; y 为去畸变后的坐标,xdistorted; ydistroted 为去畸变前的坐标。现给定参数:
![]()
以及相机内参

请根据undistort_image.cpp 文件中内容,完成对该图像的去畸变操作。
注:本题不要使用OpenCV 自带的去畸变函数,你需要自己理解去畸变的过程。我给你准备的程序中已经有了基本的提示。作为验证,去畸变后图像如图2 所示。如你所见,直线应该是直的。
undistortImage.cpp
//
// Created by daybeha on 23/10/2021.
//
#include 3 双目视差的使用
本题,你需要根据视差计算深度,进而生成点云数据。本题的数据来自Kitti 数据集。
Kitti 中的相机部分使用了一个双目模型。双目采集到左图和右图,然后我们可以通过左右视图恢复出深度。经典双目恢复深度的算法有BM(Block Matching), SGBM(Semi-Global Block Matching)等,但本题不探讨立体视觉内容(那是一个大问题)。我们假设双目计算的视差已经给定,请你根据双目模型,画出图像对应的点云,并显示到Pangolin 中。
理论部分:

1. 推导双目相机模型下,视差与 XYZ 坐标的关系式。请给出由像素坐标加视差u, v, d 推导XY Z与已知XY Z 推导u, v, d 两个关系。
①视差 d 与 XYZ 坐标的关系:
如上图, P L , P R P_L, P_R PL,PR 分别为路标点P在左右相机的投影点, O L , O R O_L, O_R OL,OR分别为左右相机的光圈中心。则 d = u L − u R d = u_L - u_R d=uL−uR
注:按图中定义, u R u_R uR 应为负数。
②像素坐标加视差u, v, d 推导 XYZ:
首先深度 z = f b d z = \frac{fb}{d} z=dfb
相机内参矩阵为K
则 x = u − c x f x z y = v − c y f y z x = \frac{u - c_x}{f_x}z\\y = \frac{v - c_y}{f_y}z x=fxu−cxzy=fyv−cyz
③ XY Z 推导u, v, d:
依旧是相机内参矩阵为K
d = f b z u = f x ∗ x z + c x v = f y ∗ y z + c y d = \frac{fb}{z}\\u = f_x*\frac{x}{z}+c_x\\v = f_y *\frac{y}{z} +c_y d=zfbu=fx∗zx+cxv=fy∗zy+cy
2. 推导在右目相机下该模型将发生什么改变。
个人理解是以 O R O_R OR 为坐标原点,此时 依旧是 u R u_R uR 应为负数。视差 d = u L − u R d = u_L - u_R d=uL−uR不变;
后两问只需保证内参矩阵K与所用相机对应,不在乎使用的是左目还是右目,因此亦不变。
编程部分:
本题给定的左右图见code/left.png 和 code/right.png,视差图亦给定,见code/right.png。双目的参数如下:
![]()
且双目左右间距(即基线)为:

请根据以上参数,计算相机数据对应的点云,并显示到Pangolin 中。程序请参考code/disparity.cpp 文件。
作为验证,生成点云应如图4 所示
disparity.cpp
//
// Created by daybeha on 23/10/2021.
//
#include double depth = fx * d / (disparity.at<uchar>(v, u));
因为disparty 为CV_8U,即uchar类型,所以该句中disparity.at(v, u)的类型也一定是uchar
如果你按书上或者GitHub中高翔老师slambook2的代码写成float, 则会有下面的运行结果:

改成double的话就更小:

不过如果选用课本《视觉SLAM十四讲》上的做法:
将直接读取的视差图:
cv::Mat disparity = cv::imread(disparity_file, 0); // disparty 为CV_8U,单位为像素
改为利用左右两图像计算,并且convertTo()第二个参数是CV_32F:
cv::Ptr<cv::StereoSGBM> sgbm = cv::StereoSGBM::create(
0, 96, 9, 8 * 9 * 9, 32 * 9 * 9, 1, 63, 10, 100, 32); // 神奇的参数
cv::Mat disparity_sgbm, disparity;
sgbm->compute(left, right, disparity_sgbm);
disparity_sgbm.convertTo(disparity, CV_32F, 1.0 / 16.0f);
则计算深度时使用的是
double depth = fx * d / (disparity.at<float>(v, u));
因为float精度更高,所以会有下面更清晰的运行结果(虚拟机结果,双系统没有跑):

4 矩阵运算微分
在优化中经常会遇到矩阵微分的问题。例如,当自变量为向量x,求标量函数u(x) 对x 的导数时,即为矩阵微分。通常线性代数教材不会深入探讨此事,这往往是矩阵论的内容。我在ppt/目录下为你准备了一份清华研究生课的矩阵论课件(仅矩阵微分部分)。阅读此ppt,回答下列问题:
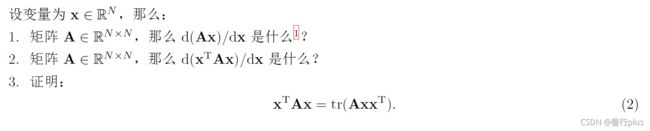
![]()
矩阵微分的重要性质:
d ( A X ) d X = d ( ( A X ) T ) d X = d ( X T A T ) d X = A T \frac{d(AX)}{dX} = \frac{d((AX)^{T})}{dX} = \frac{d(X^{T}A^{T})}{dX}=A^{T} dXd(AX)=dXd((AX)T)=dXd(XTAT)=AT
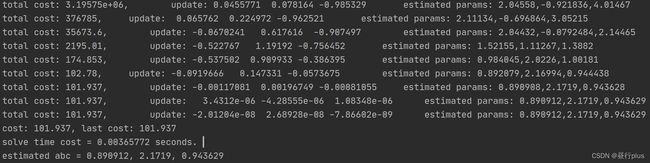
5 高斯牛顿法的曲线拟合实验
本题中你需要自己实现一遍高斯牛顿的迭代过程,求解曲线的参数。设有曲线满足以下方程:

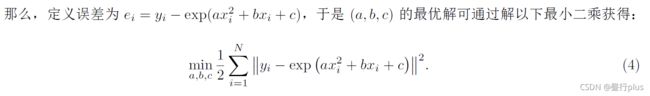

PLus 高斯牛顿法的问题:
J J T JJ^{T} JJT可能为奇异矩阵或者病态(ill-condition)的情况,此时增量的稳定性较差,导致算法不收敛。
另外畸变假设H矩阵非奇异也非病态,若求出的步长 Δ x \Delta x Δx太大,也会导致采用的局部近似式 f ( x + Δ x ) ≈ f ( x ) + J ( x ) T Δ x f(x+\Delta x)\approx f(x) + J(x)^{T}\Delta x f(x+Δx)≈f(x)+J(x)TΔx 不准确,如此我们甚至无法保证它的迭代收敛,甚至可能另目标函数变大。
gaussnewton.cpp
//
// Created by daybeha on 2021/10/28.
//
#include 6 * 批量最大似然估计


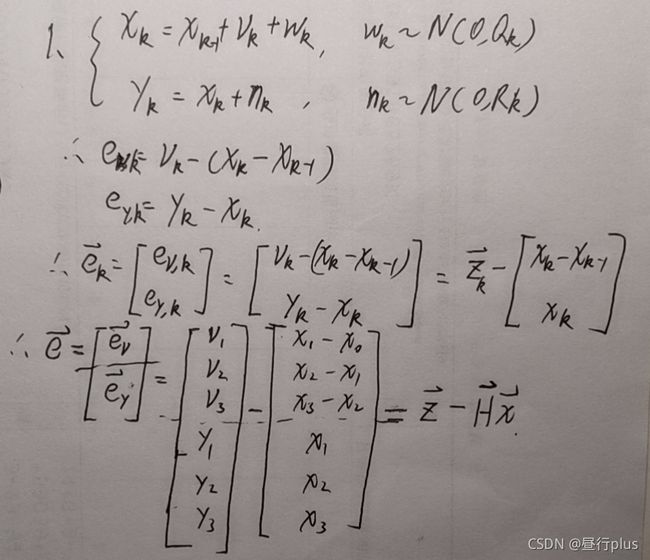
H = [ − 1 1 0 0 0 − 1 1 0 0 0 − 1 1 0 1 0 0 0 0 1 0 0 0 0 1 ] H = \begin{bmatrix} -1& 1 & 0 &0 \\ 0& -1 & 1& 0\\ 0& 0 & -1& 1\\ 0& 1 & 0& 0 \\ 0& 0 & 1& 0\\ 0& 0 & 0& 1 \end{bmatrix} H=⎣⎢⎢⎢⎢⎢⎢⎡−1000001−1010001−1010001001⎦⎥⎥⎥⎥⎥⎥⎤
注:十四讲里前三行“-1”和“1”的位置是反过来的,那个应该是个谬误
补充:
鱼眼模型与去畸变
在很多视觉SLAM 的应用里,我们都会选择广角或鱼眼相机作为主要的视觉传感器。与针孔相机不同,鱼眼相机的视野往往可以在150°以上,甚至超过180°。普通的畸变模型在鱼眼相机下工作的并不好,幸好鱼眼相机有自己定义的畸变模型。
请参阅OpenCV Fisheye文档完成以下问题:
1. 请说明鱼眼相机相比于普通针孔相机在SLAM 方面的优势。
答:相比于普通针孔相机,鱼眼相机拥有更宽阔的视野。因此可以确保在一段时间里,尽可能多的视觉特征进入相机视野,从而提高对周围环境的感知能力。
2. 请整理并描述OpenCV 中使用的鱼眼畸变模型(等距投影)是如何定义的,它与上题的畸变模型有何不同。
定义:设P为世界坐标系中坐标X的3D点(存储在矩阵X中)。相机坐标系中P的坐标向量为: X c = R X + T = ( x , y , z ) Xc=RX+T = (x, y, z) Xc=RX+T=(x,y,z)。其中R是旋转矩阵,T是偏移向量;
P的针孔投影坐标为[a, b],其中
a = x z , b = y z r 2 = a 2 + b 2 θ = a t a n ( r ) a = \frac{x}{z} , b = \frac{y}{z} \\ r^2=a^2+b^2\\ θ=atan(r) a=zx,b=zyr2=a2+b2θ=atan(r)
鱼眼畸变模型:
θ d = θ ( 1 + k 1 θ 2 + k 2 θ 4 + k 3 θ 6 + k 4 θ 8 ) θ_d=θ(1+k_1θ^2+k_2θ^4+k_3θ^6+k_4θ^8) θd=θ(1+k1θ2+k2θ4+k3θ6+k4θ8)
记畸变后的点坐标为[x’, y’],其中
x ′ = ( θ d / r ) a , y ′ = ( θ d / r ) b x′=(θ_d/r)a, y′=(θ_d/r)b x′=(θd/r)a,y′=(θd/r)b
最后,转换为像素坐标[u, v], α \alpha α为偏度系数:
u = f x ( x ′ + α y ′ ) + c x , v = f y y ′ + c y u=f_x(x′+\alpha y′)+cx, v=f_yy′+cy u=fx(x′+αy′)+cx,v=fyy′+cy
不同:上题的畸变模型包括了径向和切向两种畸变。本题的鱼眼相机只给出了 θ d θ_d θd 一种畸变类型。
3. 完成fisheye.cpp 文件中的内容。针对给定的图像,实现它的畸变校正。要求:通过手写方式实现,不允许调用OpenCV 的API。
fisheye.cpp
//
// Created by daybeha on 2022/2/2.
//
#include 4. 为什么在这张图像中,我们令畸变参数k1, . . . , k4 = 0,依然可以产生去畸变的效果?
答:取泰勒展开前五项来近似鱼眼模型,k1-k4取0,相当于只近似了第一项,所以说仍然可以完成去畸变的操作。
5. 在鱼眼模型中,去畸变是否带来了图像内容的损失?如何避免这种图像内容上的损失呢?
答:
鱼眼模型的去畸变带来了图像内容的损失。
鱼眼图一般为圆形,边缘的信息被压缩的很密,经过去除畸变后原图中间的部分会被保留的很好,而边缘位置一般都会被拉伸的很严重、视觉效果差,所以通常会进行切除,因此肯定会带来图像内容的损失。增大去畸变时图像的尺寸,或者使用单目相机和鱼眼相机图像进行融合,可以补全丢失的信息。
参考:
Opencv学习----Opencv宏定义(CV_8U、CV_8S、CV_16U…)
https://blog.csdn.net/weixin_44218240/article/details/105888149
https://blog.csdn.net/hitljy/article/details/106798632
https://blog.csdn.net/qq_21830903/article/details/95209007
https://github.com/gaoxiang12/slambook2
深蓝学院-视觉SLAM十四讲-第四章作业
视觉slam学习笔记以及课后习题《第四讲相机模型和非线性优化》