十六、异常检测
文章目录
- 1、异常检测(Anormly Detection)介绍
- 2、异常检测算法
- 3、评估异常检测算法
-
- 3.1 使用异常检测还是使用监督学习
- 4、处理异常检测的特征向量
- 5、多元(multivariate)高斯分布
-
- 5.1 利用多元高斯分布开发异常检测模型
- 5.2 原始模型和多元高斯分布模型的区别
- 5.3 选择使用原始模型 / 多元高斯模型
- THE END
1、异常检测(Anormly Detection)介绍
\qquad 异常检测是指在给定的一组无标签数据集 { x ( 1 ) , x ( 2 ) , . . . , x ( m ) } \{x(1), x(2),..., x(m)\} {x(1),x(2),...,x(m)},针对这组数据集训练一个模型 p ( x ) p(x) p(x),来判定某个数据和数据集中大多数数据之间的相似程度(某个数据落在给定数据集中心区域的概率),若某个数据 x t e s t x_{test} xtest和大多数给定数据之间很相似,则 p ( x t e s t ) ≥ ϵ p(x_{test})\geq\epsilon p(xtest)≥ϵ,说明数据无明显异常情况;否则 p ( x t e s t ) < ϵ p(x_{test})<\epsilon p(xtest)<ϵ,说明数据 x t e s t x_{test} xtest和大多数数据之间差异很大,说明给定的数据可能是一个异常数据。

\qquad 即若某个数据不落在大多数数据所在的范围之内,则这种数据出现的概率比较小,将检测出的这种数据视为异常数据。
2、异常检测算法
\qquad 首先针对 m m m个数据样本选择出 n n n个可能出现异常的特征 x j , j ∈ n x_{j},j\in n xj,j∈n;之后针对所有样本计算每一个特征的均值 μ j , j ∈ n \mu_{j},j \in n μj,j∈n和方差 σ j 2 , j ∈ n \sigma_{j}^2,j \in n σj2,j∈n;针对新给定的某个数据 x x x计算 p ( x ) p(x) p(x),若 p ( x ) < ϵ p(x)<\epsilon p(x)<ϵ,则判定数据为异常数据。异常检测算法流程如下所示:

\qquad 二维特征的异常检测的直观表示如下所示:
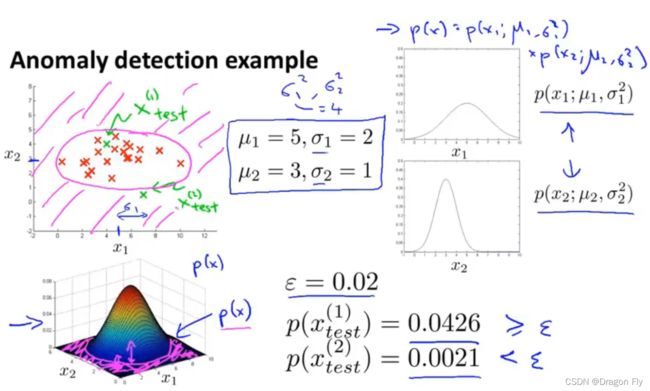
3、评估异常检测算法
\qquad 下面通过飞机引擎异常检测的例子来说明异常检测算法的评估方法:

\qquad 首先将原始数据划分为训练数据集,交叉验证数据集和测试数据集;将少部分的已知的异常数据划分到交叉验证数据集和测试数据集中,所以CV set和test set可以看做是拥有了标签的数据。

\qquad 之后根据2中介绍的高斯模型将选定的特征对训练数据集进行异常检测模型 p ( x ) p(x) p(x)的拟合;之后将拟合出的模型 p ( x ) p(x) p(x)针对CV set进行模型检测,这个检测类似于skewed data检测标准,之后根据计算出来的 F 1 F_1 F1值来判定模型的好坏,同时可以调整模型选定的特征种类和 ϵ \epsilon ϵ值的大小。最终将训练好的模型使用测试集test set来验证模型的好坏。
3.1 使用异常检测还是使用监督学习
\qquad 通常当异常样本数量很少(e.g., 0-20),但是正常样本数量很多时,适合使用异常检测;同时当不能确定异常出现的特征时,通常使用异常检测,如零部件异常检测,数据中心计算机监督;而当正常样本和异常样本数量均很多时,样本中包含充分的异常样本信息,则适合使用监督学习,如垃圾邮件检测,天气预测,疾病检测等。
4、处理异常检测的特征向量
\qquad 要使用gaussian分布来拟合异常检测模型,需要保证特征向量的数据分布满足近似高斯分布,若初始数据的特征向量不满足高斯分布,需要对数据进行变换处理,使其近似满足高斯分布,从而使算法达到更好的效果。处理方式可以取对数,取 α ∈ ( 0 , 1 ) \alpha \in(0,1) α∈(0,1)次方等。
\qquad 选择特征的方法,是可以首先选取一些特征,针对训练数据训练出一个异常检测模型,之后将模型在交叉验证数据集上进行验证,通过验证效果来增加或者减少特征数量。同时,通常选取那些在异常点取值较大或者较小的特征。
5、多元(multivariate)高斯分布
\qquad 假如有n维特征向量 x ∈ R n x \in R^n x∈Rn,多元高斯分布并非将每一维特征向量进行分别拟合 p ( x 1 ) p(x_1) p(x1)和 p ( x 2 ) p(x_2) p(x2),而是将所有的特征向量拟合成一个概率函数 p ( x ) p(x) p(x)。集合形式的高斯异常检测模型需要使用参数 μ ∈ R n \mu \in R^n μ∈Rn, Σ ∈ R ( n ∗ n ) ( 协 方 差 矩 阵 ) \Sigma \in R^{(n*n)}(协方差矩阵) Σ∈R(n∗n)(协方差矩阵),则 p ( x ; μ , Σ ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 e x p − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) p(x;\mu, \Sigma)=\frac{1}{(2\pi)^\frac{n}{2}|\Sigma|^{\frac{1}{2}}}exp^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)} p(x;μ,Σ)=(2π)2n∣Σ∣211exp−21(x−μ)TΣ−1(x−μ)
\qquad 几种多元高斯分布的图像随着 μ \mu μ和 Σ \Sigma Σ的变化情况如下所示:
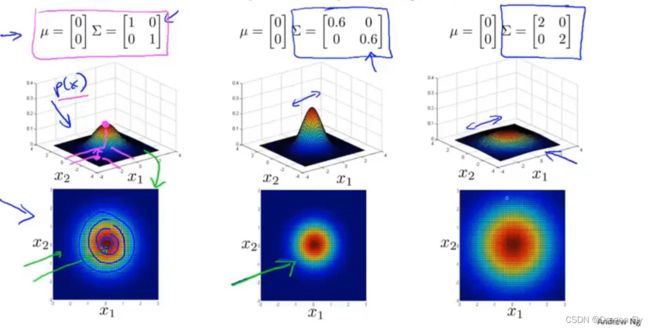
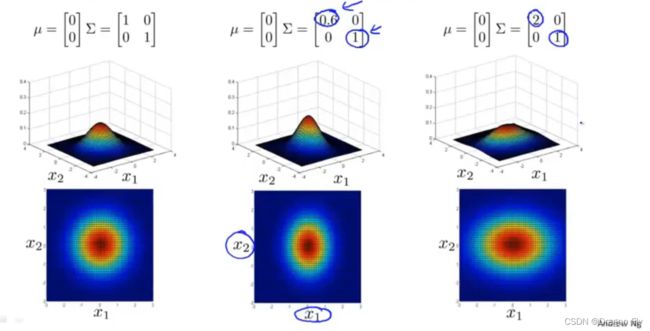

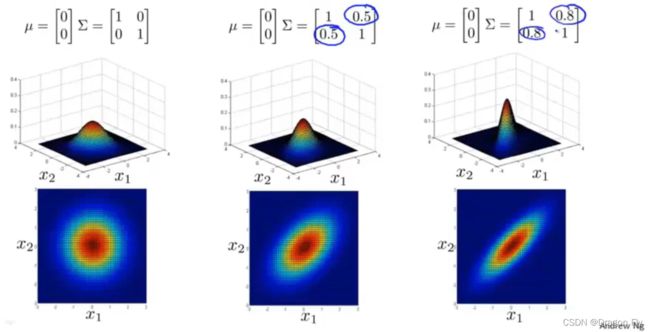
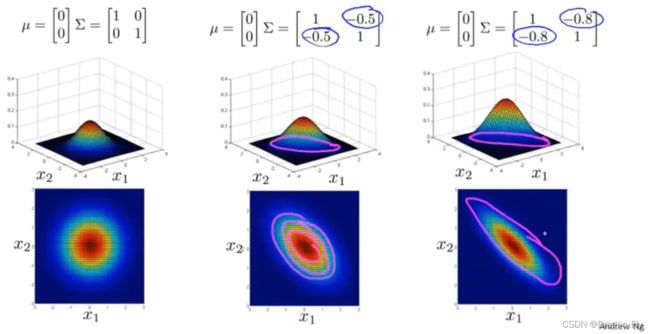
5.1 利用多元高斯分布开发异常检测模型
\qquad 给定训练集 x ( 1 ) , x ( 2 ) , . . . , x ( m ) x^{(1)},x^{(2)},...,x^{(m)} x(1),x(2),...,x(m),利用多元高斯分布构建异常检测模型的方法如下所示:

5.2 原始模型和多元高斯分布模型的区别
\qquad 将多元高斯分布模型的协方差矩阵除对角线元素外的其他元素均设置为0之后,多元高斯模型即为原模型。

5.3 选择使用原始模型 / 多元高斯模型
\qquad 原始模型需要手动选择某些特征之间的组合值异常,但多元高斯模型可以自动捕捉特征之间的相互关系;原始模型相对于多元高斯模型计算效率更高;多元高斯模型必须满足训练数据数量 m m m大于特征数量 n n n,这样才能协方差矩阵 Σ \Sigma Σ才是可逆的。

\qquad 协方差矩阵在以下两种情况下回出现不可逆的情况:若训练集中训练数据的数量少于特征数量;若特征之间有线性相关性,即有冗余特征存在。