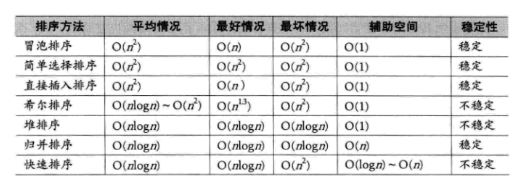
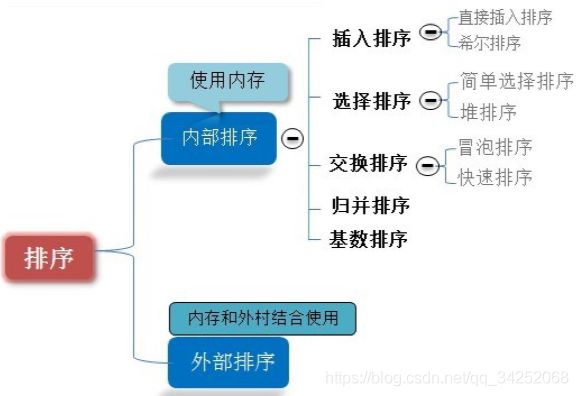
数据结构——排序算法总结（八个）

（注意⚠️：简单选择排序是不稳定的！不稳定的！不稳定的！）

内排序：指在排序期间数据对象所有存放在内存的排序。
外排序：指在排序期间所有对象太多，不能同一时候存放在内存中，必须依据排序过程的要求，不断在内，外存间移动的排序。

一、冒泡排序

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。

2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

3. 针对所有的元素重复以上的步骤，除了最后一个。持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

二、选择排序

每次选择一个最大(小)的，知道所有的元素都被输出。（选择之后需要交换位置）

三、直接插入排序

插入排序的基本方法是：每一步将一个待排序的元素，按其排序码的大小，插入到前面已经排好序的一组元素的适当位置上去，直到元素全部插入为止

算法思路：

当插入第i(i >= 1)时，前面的V[0]，V[1]，……，V[i-1]已经排好序。这时，用V[I]的排序码与V[i-1]，V[i-2]，…的排序码顺序进行比较，找到插入位置即将V[i]插入，原来位置上的元素向后顺移。

以[21,25,49,25,16,08]为例，排序过程如下所示：

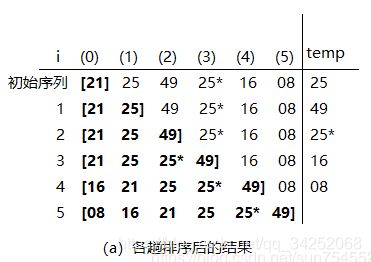
在小规模数据集或是基本有序时，该算法效率较高。

四、希尔排序

先对数据进行预处理，使其基本有序，然后再用直接插入排序算法排序。

五、快速排序

利用“分而治之”的思想对集合进行排序

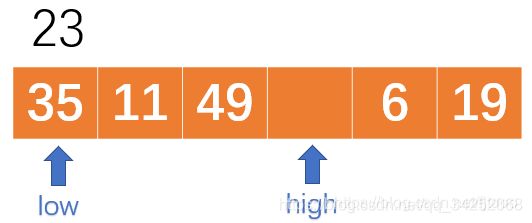
假设序列为23，11，49，35，6，19.

我们用low和high分别指向第一个元素和最后一个元素，同时我们取第一个数23为“中枢元素”，将它“挖”出来，如下：

将23挖出来以后，最左边就留下了一个“坑”，根据我们之前所说的，我们要把比中枢元素（23）大的扔到左边，所以我们就要用high来找比23大的值，将它扔到之前在左边挖好的坑里。现在，19比23小，19就不用动，因为我们本来就是要把比23小的数留在右边。那么将high左移一位继续，6也比23小，high再左移一位，发现35比23大，那么就把它填进左边的坑里，如下：

此时high所指的位置也留下了一个坑，那么我们就用low在序列头部开始找比23小的数来扔到右边，35比23大，low右移一位，发现11比23小，所以将11填到右边的坑里，如下：

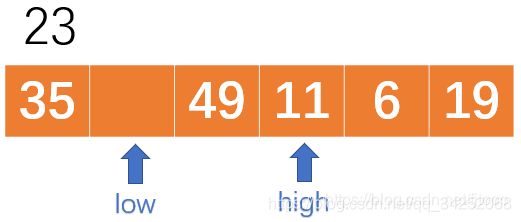
继续从high开始，往左找比23大的数，找到49，往左边填坑，如下：

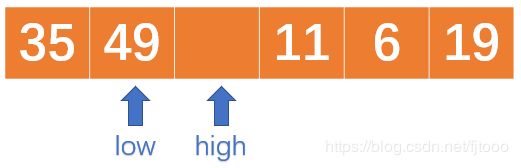
继续从low开始，往右边找，发现此时 low与high相遇了，那么这个地方就是中枢元素“归位”的位置，如下：

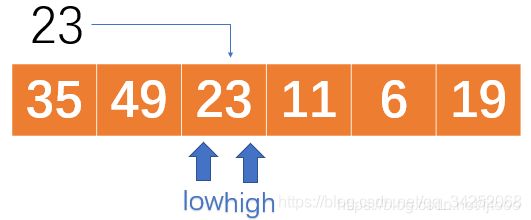
好了，通过以上过程，我们已经将比23小的数扔到了右边，大的数扔到了左边。
此后，将以23为分界线的左右两个子序列继续重复此过程，直到所有子序列仅有一个元素为止，排序完成。

六、堆排序

堆：堆是满足下列性质的完全二叉树：

• 每个节点都大于或是等于其左右孩子节点的值，称为大顶堆
• 每个节点都小于或是等于其左右孩子节点的值，称为小顶堆

接下来说下堆是如何做排序的，思路如下（以大顶堆为例）：

1. 根节点是整个堆的最大值，将它移走。
2. 将剩余n-1个节点重新构造成一个堆，再将根节点移走
3. 重复执行1,2。直到没有节点可移动，就生成了有序序列。

该算法有两个需要解决问题：

1. 如何将一个无序序列构建一个堆。
2. 移除根节点后，如何用剩余的节点重建堆

基本思路：
堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

七、归并排序

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。
分而治之

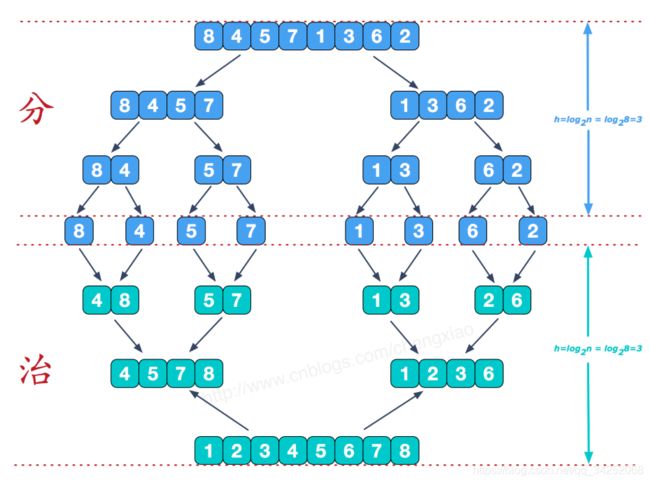
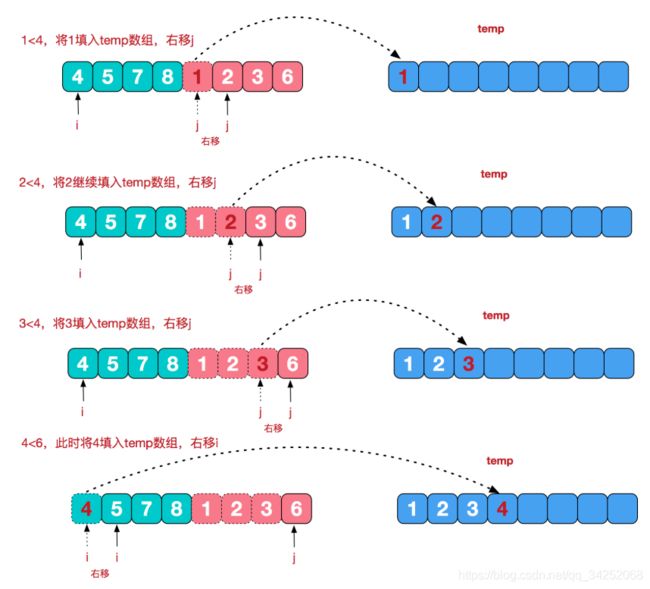
合并相邻有序子序列
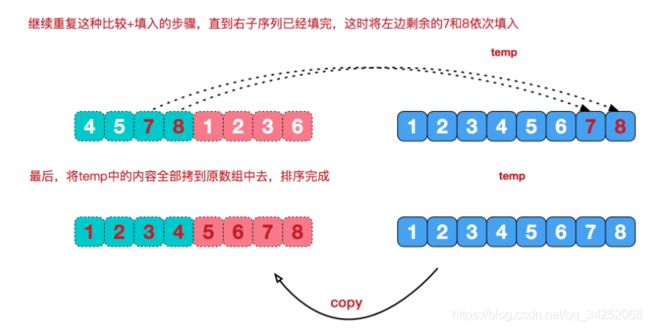
再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

八、基数排序

基数排序与前面的七种排序方法都不同，它不需要比较关键字的大小。

它是根据关键字中各位的值，通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。

基本思想

设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。

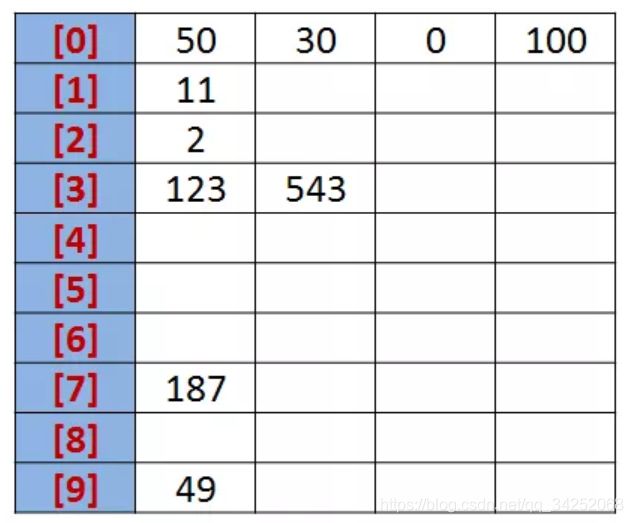
我们知道，任何一个阿拉伯数，它的各个位数上的基数都是以0_{9来表示的。所以我们不妨把0}9视为10个桶。

我们先根据序列的个位数的数字来进行分类，将其分到指定的桶中。例如：R[0] = 50，个位数上是0，将这个数存入编号为0的桶中。分类后，我们在从各个桶中，将这些数按照从编号0到编号9的顺序依次将所有数取出来。这时，得到的序列就是个位数上呈递增趋势的序列。 按照个位数排序： {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。

接下来，可以对十位数、百位数也按照这种方法进行排序，最后就能得到排序完成的序列。

过程可参考：https://baijiahao.baidu.com/s?id=1653077762711837226&wfr=spider&for=pc