马毅：低维模型与深度模型的殊途同归

作者：邱陆陆

上周，今日头条人工智能实验室在清华大学举办了第二期 AI 技术沙龙，邀请到上海科技大学信息科学与技术学院的马毅教授带来题为「高维数据的低维结构与深度模型」的主题分享。马毅教授以计算机视觉为例，展示了低维模型和深度模型如何从不同角度试图攻克同一个问题：高维数据的信息提取。并且详细展示了从低维模型角度如何分解并逐步攻克这个问题，有哪些应用，以及低维模型如何给深度模型带来可解释性。以下为机器之心对讲座内容进行的整理。

对于做机器学习，和做图像视觉的研究者来说，过去的十年是非常激动人心的十年。以我个人来讲，非常有幸接触了两件事情：第一件是压缩感知（compressive sensing），高维空间的低维模型，利用其稀疏低秩的性质，带来一场图像处理的革命。第二件就是大家非常熟悉的深度学习。今天我以视觉为例，探讨低维模型和深度模型如何为了一个共同的目的从两个完全对立的方向走到了一起。

从结果来看，压缩感知和深度学习都让我们能在像素级别处理图像的全局信息。而从方法论来看，这二者是互补的。压缩感知完全基于模型（model-based），有很好的结构，经过严谨的数学建模。深度学习则完全反过来，模型非常灵活，需要通过数据进行监督学习，是一种基于实证的方法。更有趣的是，二者取得突破的原因也和方法论一样完全对等。压缩感知的突破来自数学纯理论的突破，深度学习的突破则来自于应用和经验，结果是都得到了同样强大而可扩展的算法，而且其结构和流程都非常相似。

很多人觉得压缩感知和深度学习是完全不同的东西，两个领域的研究者互不理解。然而 CNN 的发明者 Yann LeCun 在深度学习流行起来之前就在做压缩感知，自编码器（autoencoder）就是从压缩感知来的概念。今天我希望讲解这二者螺旋发展的历史过程，和大家分享一些经验和教训。

背景

大数据的「大」体现在两个方面，量多、维度高。然而数据再大也不是随机的，它们通过结构承载信息。高维数据并不填满整个空间，由于存在特定的生成机制，其自由度其实很低。在图像里，这些特点是能被「看」到的：诸如对称性、周期性这样规律在图像的局部和整体都有体现。

如何通过数学建模量化描述这些特点呢？举个例子，把一张图像用 100*100 的矩阵表示，线性代数告诉我们，周期性会使它的各列线性相关，矩阵的秩肯定比矩阵的规模小很多，可能只有 10。也就是说，如果你把每一列看成一个向量，看成一个 100 维空间中的点，当我们把这些点画出来，会发现他们不是散布得到处都是，而是集中在某一个子空间中，这个子空间就是我们要找的低维结构。如果我的数据来自上述的低秩结构，哪怕加上一些高斯噪声，我只需要对矩阵做做奇异值分解（SVD），把小的奇异值扔掉，就能得到包含的主要信息。这个过程在统计里面也叫 PCA（主成分分析），有超过 100 年的历史了。全世界计算机运行起来，大部分电费就花在做这件事上。谷歌的工作就是解线性方程、找特征向量、算佩奇排名（PageRank）。这个方法的弱点在于不鲁棒，如果矩阵中的数据有随机损毁，算出来的子空间就会和真实情况（ground truth）差很远，因此大家都在想办法提高系统的鲁棒性。

我们已经有了信号处理、信息理论，为什么还要学习压缩感知和深度学习？因为工程实践变了。信息理论是上世纪五、六十年代的发明，那时候的工程实践是由工程师掌控全过程的。工程师从布置传感器采集数据开始参与全程，花了大量时间在降噪，如果行不通，就从数据收集开始重头再来。但是现今的数据科学家面对的工程实践条件完全不同，我们使用的数据极少有自己采集的，采集数据时也没有目的性。因此数据中有大量的缺失、损毁、变形，使得原来的数据处理方法变得有局限乃至于失效。今天我们不能因为做人脸识别的时候遇到一位女士带着墨镜无法识别就把她找回来重新拍一张照片、不能因为做三维重建的时候树挡住了建筑物就把树砍掉，我们要学会处理这样不完美的数据。旧的方法行不通并不代表数据中不含有正确的信息，只不过需要我们发现新的理论和方法，从不完美的数据中把信息提取出来。

理论：稀疏和低秩的信息恢复

原来解线性方程的时候方程数一定要多于未知量，参数矩阵 L 是长的，噪声则用高斯的方法求个最小方差。这个方法有两百年历史。1756 年，Boscovich 提出，如果噪声不是高斯的话，应该用一范数而不是二范数。有趣的是高斯是这篇文章的评审人，他评价道，「如果噪声比较大的时候一范数的效果确实比较好。」当时这只是一个想法，并没有相应的理论。

现在我们要应对的问题是，未知量远比方程数多。以前处理这种问题的方法是等，天文学家可以等待十年只为看到一个现象。现在大家等不及了，要从不全而且有损毁的数据中找到这种信息。如何寻找呢？求解此类方程不幸是个 NP 困难的问题，因此之前没人关注。然而常见的高维数据有稀疏的特点，即 x 不是所有维度都有值，只有少数非零。大约十年前，陶哲轩和 Candès 发表了文章，发现这类方程在很宽松的条件下可以用一范数求解，算法是可在多项式时间内完成的（polynomial）。

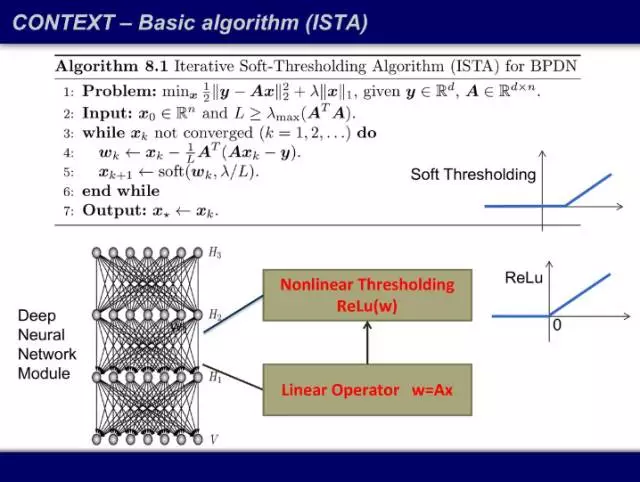
解下方用一范数惩罚过的方程（其中 x 有稀疏要求），然后进行迭代。将上一次迭代算出的 x 带入做一个线性变换，得到 w，w 经过一个软阈值函数（soft thresholding）后就得到这一次迭代的输出 x，重复该过程直到收敛。熟悉深度学习的同学会发现，如果我把用词改一改，把一次「迭代」叫做一个「层」，然后把这个迭代过程画出来，我们得到的结构是线性算子加阈值函数，而且阈值函数的样子和激活函数 ReLU 长得很像——这就是一个神经网络。

完全从模型推导出来的最优的、收敛速度最快的算法，和深度学习通过经验找到的神经网络非常相似。

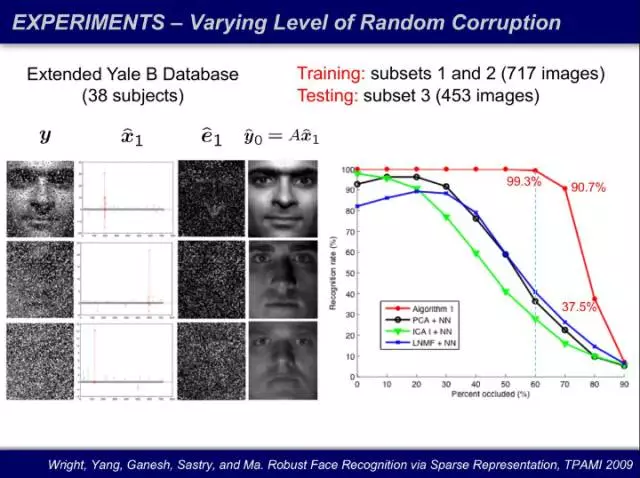
这些理论可以被用于图像处理。我们将人脸识别表示成一个线性方程，把一张人脸图像表达为一个库的线性叠加（x），把我表达不了的像素当成误差剔除出去（e）。其中 x 和 e 都是未知的，未知量个数远超过方程数。我们还将像素随机损毁，损毁 60% 的像素后，人已经无法对人脸进行识别，然而计算机仍然识别并实现接近百分之百的恢复。

这个例子让我们很震惊：在高维的世界里，数据携带的信息是我们难以想象的鲁棒的。有多鲁棒呢？随着图像的分辨率越来越高，你可以损毁的像素的比例可以无限接近百分之百。这是数学的神奇之处：我们本来只想要损毁一小部分像素，但得到了远远超出想象的结论。

这些理论刚出现的时候，陶哲轩等人都是不相信的。高维空间的统计和几何现象和低维空间中发展的几何和统计的直觉是完全相反的。你认为在低维空间一定会发生的事情在高维空间基本不发生，你认为在低维空间中绝对不会发生的事情往往在高维空间中以概率为 1 发生，即使世界一流的数学家在此也会犯错，这是我们学到的极其宝贵的经验。

我们也可以把一维的稀疏向量的上述性质扩展到二维的低秩矩阵：如何很少的特征把矩阵表示出来？互联网都靠解决这个问题吃饭。无论是淘宝还是脸书，都面临着同一个的问题：我只有关于用户的部分信息，我需要根据这些不完整的信息猜测一个人对一样事物是否感兴趣，有多感兴趣。这就是一个矩阵恢复问题，我们要「把表填满」。

有些同学可能会问，我们做深度学习的人为什么要关注这个问题？因为这实际上是一个普遍的问题，不管你用任何方法，只要你想通过观测来恢复隐藏节点，它的本质就会回到同一个问题：从低秩、稀疏的数据中找到信息。就像陶哲轩说过，「物理里面有能量守恒，数学中有难度守恒。」你可以使用任何启发式（heuristic）方法，但是核心必须是解决这个问题。什么是低秩？就是模型的自由度少。什么是稀疏？稀疏代表网络为零的项特别多。所有为零的项都代表了网络的条件独立性（conditional independence）。

如何解决这个问题？与深度学习从应用到算法的路相反，还有一条从理论到算法再到应用的路。

我们把过程拆分为两步：

• 第一，寻找矩阵的秩最小化这个 NP 困难的问题的可计算（tractable）条件。

• 第二，在可计算的条件下寻找最快的、不能再优化的算法。

很长时间内，大家的办法都是启发式的，好用就是好用，也不知道为什么好用。压缩感知告诉我们，不要试图最小化 0 范式，要最小化它的凸包（convex hull）。矩阵的秩的凸包就是它的核范数（nuclear norm），即奇异值的和，就像 0 范数的凸包就是 1 范数（绝对值的和）。最小化凸包问题是一个凸优化问题，可以证明，该问题可以用多项式算法完成。

接下来就需要寻找凸优化的解和原问题的解在什么条件下是一致的了。我们做了一些模拟，结果非常令人振奋。

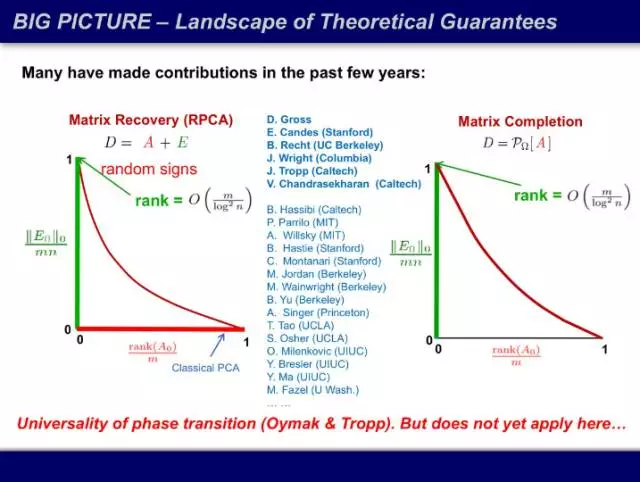
下图中，横轴是秩占矩阵规模的比例，纵轴是损毁比例，在不同的比例里面我们多次求凸优化的解，看看凸优化的解和原问题的解是否一致。白色区域意味着所有模拟的解都一致，黑色区域代表所有模拟的解都不一致。之前我们认为整个区域都是黑的，这个 NP 困难的问题无法求解，结果发现了非常漂亮的相变过程，在曲线上，凸优化的解完全可用。而可用区域也刚好是工程实践最关心的区域：数据确实有结构，损毁也没那么严重。

当矩阵的秩足够小，同时损毁足够少时，凸优化几乎可以恢复任何矩阵。原来还要设定损毁的权重因子 λ 并交叉检验，现在做完数学分析后连 λ 都不用设，直接用 1/√m，整个算法没有任何自由参数。对于任何一个凸函数，只有一个全局最小值，而且找到了就是最优解。同时我也不需要矩阵的全部信息，给我 10% 甚至更少的信息就够了，随着矩阵越大，需要的信息占比就越小。能够接受的损毁上限在哪里？当误差的符号是随机的时候，随着矩阵越来越大，可以损毁的比例接近 100%。当你的数据足够高维，你几乎可以随意损毁，信息仍然在，而且可以用很鲁棒的算法把信息都找到。

刚才的矩阵修复定理证明了下图的绿线，传统 PCA 是横轴的红线，模拟显示，红色曲线下方的区域都有效，但尚未有理论证明。

理论的突破让大家兴奋了一阵子随即冷静了下来：可计算并不等于实用。一张 1000*1000 的图片约一兆大小，D = A + E，A 和 E 都不知道时，这个优化问题的维度是两百万，而且目标函数不可导。传统凸优化方法解几百维的问题还好，数百万维的问题，参数连存都存不下。因此只能用一阶算法，不能用二阶算法。这和神经网络是一样的，你只能用随机梯度下降（stochastic gradient descent）去训练上千万个未知量。

一阶算法的问题是，虽然可扩展（scalable），但是收敛速度非常慢，大概要 1 万次迭代才能收敛。因此我们首先想到特殊解：固定 A 求 E 和固定 E 求 A 都是有闭解的，我们利用临近算子（proximal operator）做阈值。我们在寻找一阶算法的时候发现，80 年代的比 90 年代的快，70 年代的比 80 年代的快，最后最快的算法是 50 年代的 ADMM（Alternating Direction Method of Multipliers），而且现在训练神经网络的也是用 ADMM 做分布和并行。这些算法快是因为当年的算力有限，数学家们还拿着计算尺在做运算。现在模型强调越大越好越深越好，是因为资源丰富了，它并不在乎效率问题了，人工、时间、计算能力，都不计成本地投入。在传统优化领域我们不是这样做的，我们将 1 万次迭代缩减到 20 次迭代。这就等价于原本要建 8000 层的神经网络，现在用了 20 层就实现了。

最快的算法有什么结构呢？它的信息流为什么如此有效呢？我们给 A 矩阵和 E 矩阵添加一个拉格朗日算子，强化 D = A + E 的约束条件。迭代过程也是线性变换和非线性阈值计算。拉格朗日算子的更新过程和残差神经网络完全一样。又一次，两条完全不同的路通向了同一个结果：纯由模型推导得出的、基于两百年前拉格朗日发明的，有约束的优化问题（constrained optimization）得到的最有效的迭代算法和我们通过机器学习在大量的网络结构中筛选，大浪淘沙，试各种超参数（hyperparameter）试出来的结构残差神经网络一模一样。

做深度学习的同学可能之前不知道为什么深度神经网络、残差神经网络这么神奇，今天回去你可以理直气壮地说：这不就是有约束优化问题吗！我要找出的就是低维结构，而且这些结构一定满足这些条件。拉格朗日算子就是要以这种方式更新，这就是最有效的方法。虽然不是很严格，低维模型为神经网络的有效性提供了一个可能的解释。

因此大家看文献不要只看过去两三个月的，人类的历史这么长，有太多宝贵的思路已经被想过了，太多高效的工具已经被发明过了。我们今天遇到的问题，前人们在控制领域、优化领域早就遇到过了，适用范围不同，然而本质不变。

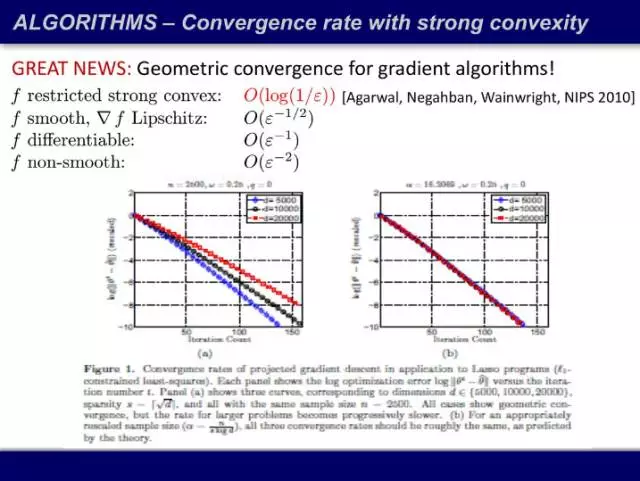
新的问题：为什么收敛这么快？它的收敛速度明明应该很慢，是 O(k^(-2))，为什么 20 次迭代就够了？Agarwal 证明了，我们对这一类问题在高维空间的认识又是有局限性的。在高维空间如果你的目标函数满足限制性强凸条件（restricted strong convex），一阶算法的收敛速度和二阶算法的收敛速度一样，就是指数的。

应用

上述理论有十分广泛的应用。在视觉方面，有：

从有部分测量缺失的结构化图像中恢复低维结构：低秩纹理修复（Liang, Ren, Zhang, and Ma, in ECCV 2012）；不同光线条件下立体结构修复（Wu, Ganesh, Li, Matsushita, and Ma, in ACCV 2010.）；从视频帧中做背景修复（Candès, Li, Ma, and Wright, JACM, May 2011.）等。

从有部分测量损坏的结构化图像中恢复低维结构：从移动摄像机的图像中得到全景（Panorama）（Zhou, Min, and Ma, in 2012)等。

从非线性形变和线性压缩采样中恢复低维结构：从旋转、扭曲过的图片中提取几何形状和纹理（Zhang, Liang, Ganesh, Ma, ACCV'10, IJCV'12.）；有径向形变的相机位置校准、曲面形状恢复（Zhang, Liang, and Ma, in ICCV 2011.）；虚拟现实（Zhang, Liang, and Ma, in ICCV 2011）；城市场景的整体三维重建（Mobahi, Zhou, and Ma, in ICCV 2011.）；人脸检测（Peng, Ganesh, Wright, Ma, CVPR'10, TPAMI'11）；物体对正（Rectifying）（Zhang, Liang, Ganesh, Ma, ACCV'10 and IJCV'12.）；超分辨率（Carlos Fernandez and Emmanuel Candes of Stanford, ICCV2013.）等。

在视觉领域之外，也有很多例子，比如：文本主题建模，把文中的词分为低秩主题「背景」和有信息量的、有区分度的「关键词」（Min, Zhang, Wright, Ma, CIKM 2010.）；时间序列基因表达（Chang, Korkola, Amin, Tomlin of Berkeley, BiorXiv, 2014.）；音频中低秩的背景音和稀疏的人声的分离（Po-Sen Huang, Scott Chen, Paris Smaragdis, Mark Hasegawa-Johnson of UIUC, ICASSP 2012.）；互联网流量数据异常检测（Mardani, Mateos, and Giannadis of Minnesota, Trans. Information Theory, 2013.）；有遮挡的 GPS 信号恢复（Dynamical System Identification, Maryan Fazel, Stephen Boyd, 2000.）等。

结论

稀疏和低秩是高维空间中一大类低维模型的两个特例。事实上有一大类低维结构都有很好的性质，可以用很少的度量（measurement）很鲁棒地恢复出来。这种结构的特性叫可分解性（decomposable）。

我们知道图像是由小的元素组成的，它们可以分开也可以相加，然而大家还不清楚这些结构和图像中实际的结构是如何对应的。从这个意义上来说，理论是超前于应用的，还需要大家继续探索。

低维模型和深度神经网络的联系

压缩感知对深度学习的指导意义有以下这三个方面。

第一个问题，一层神经网络能做什么？最好能做到什么程度？

Yann LeCun 最早做的 autoencoder 就是这个思路。给定一个数据（Y），如何找到一个一层的线性变换（Q），使得变换后数据（X）最稀疏、维数最低。信号处理就是找到傅里叶变换（FT）或离散余弦变换（DCT）使得我的数据变得尽可能的可压缩。

现在问题变成找到一个「黄金变换」，让我的数据最可压缩。这个问题的难点在于，这是一个非凸、非线性问题。Y ≈ Q * X，其中 Q 和 X 都不知道，而且通常对 Q 还有很多额外的结构上的要求（比如正交性）。之前的做法都是启发式的，固定 Q 找 X 或者反过来。甚至很长时间大家认为找这样的结构是没有意义的：即使找到了 Q，所需的数据也是指数倍的。如果 Q 是一个 n*n 矩阵，X 的秩是 k，那么 Y 需要的样本数就至少是从 n 选 k，是一个 n 和 k 的指数倍量级。15 年，哥伦比亚的学者发现：第一，需要的数据不用指数倍，达到 n^3 即可，第二，稀疏程度小于 1/3，满足上述两条件的情况下，利用 70 年代的信赖域算法（Trust Region Method），就能保证找到全局最优的变换。

第二个问题，神经网络如何找到全局最优解？

深度神经网络可以分解为串联的矩阵操作，14 年，CMU 的学者证明，如果你通过训练找到的网络参数足够稀疏，那么对于优化函数来说就是全局最优的。这就解释了 Hinton 当年为什么能通过 Dropout 让深度神经网络变得真正可用。可以看出稀疏矩阵和深度学习之间是有根本性联系的。

第三个问题，「深度」是神经网络的必要条件吗？浅层神经网络的局限性在哪里？

学控制的同学知道，控制有两招：如果对系统了解得很透彻，用前置控制器（feedforward）即可；如果对系统的了解有很多误差，则通过反馈（feedback）进行控制。把前馈和反馈用机器学习的语言表达，就是无监督学习和监督学习。

为了证明深度的必要性，我们打算先搭建一个最简单的网络结构 PCANet 做基线：两层的 PCA 筛选器，激活函数用比 ReLU 还简单的 Binary，并且直方图统计（histogram）替代均值或者最大值池化输出。结果很震惊：这个结构 15 年在 FERET 数据库上成为了当前最佳（state-of-art）。

今年的 ICLR 最佳论文，伯克利和 MIT 的研究者就用了两层神经网络，加上核方法（kernel），不需要任何反向传播，在 CIFAR10 上达到了和 ResNet 差一个点的效果，而他们的网络实现起来只需要 3 分钟，而 Inception 这种神经网络至少需要一两天。

结语与扩展

现在计算能力上来了，数据更多了，然而这只代表我们有更丰富的资源了，什么是处理海量高维数据真正有壁垒的技术，什么样的算法是可用的、可迁移的、可扩展的，才是值得我们思考的问题。

今天我们讲了在一个子空间上如何鲁棒地高效地寻找一个低维结构，如果数据分布在多个子空间，涉及到无监督学习，如何把数据分到不同子空间。这也是 Yann LeCun 等一系列学者所说的，机器学习的未来就是从监督学习到无监督学习。在效率上，强化学习的效率最低，每次实验只生成一个比特的信息（成功、不成功），监督学习每一批大概总结几十个比特的信息，非监督学习，要生成一张图所需的信息量就非常大。如果能通过无监督的方法把结构找出来，算法的效率会大幅提高，计算的成本会大幅降低。如果未来机器学习以效率优先为目标，那么一定会从监督学习到无监督学习，从深的模型到浅的模型，从大的模型到小的模型，从大的数据到小的数据。

爱因斯坦说，「Everything should be made as simple as possible, but no simpler.」。这是科学和工程领域共同的奋斗目标：深刻的应该是我们对问题的理解，而不是模型本身。

本文为机器之心原创，转载自“机器之心”微信公公众号。