CV笔记|图像处理：Harris特征点检测器——兴趣点检测

1 基础知识

1.1 特征点检测

在拼图游戏中，我们一般从有明显特征的碎片入手，因为区分度比较高的特征片段提供了图像丰富的信息，更容易用于定位。在计算机视觉和图像处理中，使用计算机提取图像信息，决定每个图像的点是否属于一个图像特征称为特征点检测。

特征点检测广泛应用于目标匹配、目标跟踪、三维重建等应用中，在进行目标建模时会对图像进行目标特征的提取，常用的有颜色、角点、特征点、轮廓、纹理等特征。角点特征是图像中较好的特征，比边缘特征更好地用于定位。

1.2 角点

在现实世界中，角点对应于物体的拐角，道路的十字路口、丁字路口等。从图像分析的角度来定义角点可以有以下两种定义：

1. 角点可以是两个边缘的角点；
2. 角点是邻域内具有两个主方向的特征点。

人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。

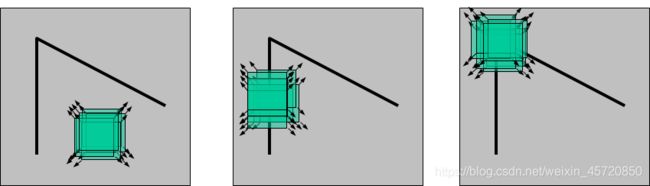
1. 如果这个特定的窗口在图像各个方向上移动时，窗口内图像的灰度没有发生变化，那么窗口内就不存在角点，如左图，表示一个平坦区域；
2. 如果窗口在某一个方向移动时，窗口内图像的灰度发生了较大的变化，而在另一些方向上没有发生变化，那么窗口内的图像可能是一条直线的线段，如中图，表示一个边缘特征（Edges）；
3. 如果在各个方向上移动这个特征的小窗口，窗口内区域的灰度发生了较大的变化，那么就认为在窗口内遇到了角点（Corners），如右图。

1.3 图像梯度

“灰度/像素值发生很大变化”这一现象可以用图像梯度进行描述。在图像局部范围内，图像梯度越大表示该局部内像素值变化越大（灰度的变化率越大）。图像的梯度在数学上可用微分或者导数来表示。对于数字图像来说，相当于是二维离散函数求梯度，并使用差分来近似导数： $$G_x(x,y)=H(x+1,y)-H(x-1,y)$$ $$G_y(x,y)=H(x,y+1)-H(x,y-1)$$ 在实际操作中，对图像求梯度通常是考虑图像的每个像素的某个邻域内的灰度变化，因此通常对原始图像中像素某个邻域设置梯度算子，然后采用小区域模板进行卷积来计算，常用的有Prewitt算子、Sobel算子、Robinson算子、Laplace算子等。

2 Harris角点检测基本原理

Harris角点检测是一种常用的、较为基础的特征点检测方法，可用于判断角点、边缘、平滑区域。Harris角点检测原理是利用移动的窗口在图像中计算灰度变化值，其中关键流程包括转化为灰度图像、计算差分图像、高斯平滑、计算局部极值、确认角点。

2.1 建立数学模型

通过建立数学模型，判断哪些窗口会引起较大的灰度值变化。

让一个窗口的中心位于灰度图像位置$(x,y)$，将该处像素灰度值记为$I(x,y)$ ，如果让该窗口在点$(x,y)$处平移$(\Delta x,\Delta y)$到新的位置 $(u,v)$ ，新位置处的像素灰度值就是$I(u,v)$ 。$|I(u,v)-I(x,y)|$就是窗口移动引起的灰度值的变化值。

设$w(x,y)$为$(x,y)$处的窗口函数，其表示窗口内各像素的权重，为了简化模型可以把窗口内所有像素的权重都设为1，即一个均值滤波核。也可以把 $w(x,y)$设定为以窗口中心为原点的高斯分布，即一个高斯核。如果窗口中心点像素是角点，那么窗口移动前后，中心点的灰度值变化非常大，所以该点权重系数应该设大一点；离窗口中心（角点）较远的点灰度变化比较小，将权重系数设小一点。

对于图像$I(x,y)$，当中心位于点$(x,y)$处的窗口向各个方向平移$(\Delta x,\Delta y)$时，为描述像素灰度值的变化，引入$E(x,y)$：
$$E(x,y;\Delta x,\Delta y)=\sum _{(x,y)}w(x,y)\times [I(x+\Delta x,y+\Delta y)–I(x,y){]}^2$$

其中，$w(x,y)$是以点$(x,y)$为中心的窗口，为加权函数，它既可是常数，也可以是高斯加权函数。

若窗口内是一个角点，则上式中平方项会很大，相应地，$E(x,y)$的计算结果将会很大。

根据泰勒展开，对图像$I(x,y)$在平移$(\Delta x,\Delta y)$后进行一阶近似：

$$\begin{array}{rl}I(x+\Delta x,y+\Delta y)& =I(x,y)+I_x(x,y)\Delta x+I_y(x,y)\Delta y+O(\Delta x^2,\Delta y^2)\\ & \approx I(x,y)+I_x(x,y)\Delta x+I_y(x,y)\Delta y\end{array}$$

其中，$I_x,I_y$是$I(x,y)$的偏导，在图像中就是求$x$ 和 $y$ 方向的梯度图：

$$I_x=\frac{\partial I(x,y)}{\partial x},I_y=\frac{\partial I(x,y)}{\partial y}$$

$$\therefore E(x,y)=\sum _{(x,y)}w(x,y)\times [I(x,y)+I_x\Delta x+I_y\Delta x-I(x,y){]}^2$$进一步化简得到：

$$E(x,y;\Delta x,\Delta y)\approx \sum _{(x,y)}w(x,y)[I_x(x,y)\Delta x+I_y(x,y)\Delta y{]}^2=[\Delta x,\Delta y]M(x,y)\left[\begin{array}{c}\Delta x\\ \Delta y\end{array}\right]$$

其中
$$\begin{array}{rl}M(x,y)& =\sum _{(x,y)}\left[\begin{array}{cc}{I}_x(x,y{)}^2& I_x(x,y)I_y(x,y)\\ I_x(x,y)I_y(x,y)& I_y(x,y{)}^2\end{array}\right]\\ & =\left[\begin{array}{cc}{\sum }_{(x,y)}{I}_x(x,y{)}^2& {\sum }_{(x,y)}{I}_x(x,y)I_y(x,y)\\ {\sum }_{(x,y)}{I}_x(x,y)I_y(x,y)& {\sum }_{(x,y)}{I}_y(x,y{)}^2\end{array}\right]\end{array}$$

经过上述步骤，我们得到了一个实对称对角矩阵$M$，将其进一步对角化：
$$M=R^{-1}\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]R$$

其中，$R$ 为角点响应函数，通过判定其大小来判断像素是否为角点；${\lambda }_1,{\lambda }_2$为特征值。

$$R=det(M)-k(trace(M){)}^2$$

其中 $det(M)={\lambda }_1{\lambda }_2$是矩阵 $M$ 的行列式， $trace(M)={\lambda }_1+{\lambda }_2$ 是矩阵 $M$ 的迹, $k$是一个经验常数，通常取值在0.04~0.06之间。

因为特征值 ${\lambda }_1$ 和 ${\lambda }_2$ 决定了 $R$ 的值，所以我们可以用特征值来决定一个窗口是平坦区域、边缘还是角点：

• 平坦区域：该窗口在平坦区域上滑动，窗口内的灰度值基本不会发生变化，所以 $|R|$ 值非常小，在水平和竖直方向的变化量均较小，即 $I_x$和 $I_y$都较小，也就是 ${\lambda }_1$ 和 ${\lambda }_2$ 都较小；
• 边缘：$|R|$值为负数，仅在水平或竖直方向有较大的变化量，即 $I_x$和 $I_y$只有一个较大，也就是 ${\lambda }_1\gg {\lambda }_2$ 或 ${\lambda }_1\ll {\lambda }_2$；
• 角点：$|R|$ 值很大，在水平、竖直两个方向上变化均较大的点，即 $I_x$和 $I_y$ 都较大，也就是 ${\lambda }_1$ 和 ${\lambda }_2$ 都很大。

为了得到最优的角点，我们使用非极大值抑制。应当注意的是，Harris 检测器具有旋转不变性，但不具有尺度不变性，也就是说尺度变化可能会导致角点变为边缘（P.S.：SIFT特征具有尺度不变性）。

注记：实对称矩阵一定可以对角化

定理：设 $A$ 为 $n$ 阶实对称矩阵，则必有正交矩阵 $P$，使 $P^{-1}AP=B$，其中 $B$ 是以 $A$ 的 $n$ 个特征值为主对角线元素的对角矩阵。

3 基于OpenCV的实现

在OpenCV中有提供实现Harris角点检测的函数 cv2.cornerHarris，我们可以直接调用。

函数原型：cv2.cornerHarris(src, blockSize, ksize, k[, dst[, borderType]])

对于每一个像素 $(x,y)$，在 $(blockSize\times blockSize)$ 邻域内，计算梯度图的协方差矩阵 $M(x,y)$，然后通过上述角点响应函数得到结果图，输出图中的局部最大值对应图像中的角点。

参数解释：

• src - 输入灰度图像，float32类型
• blockSize - 用于角点检测的邻域大小，就是上面提到的窗口的尺寸
• ksize - 用于计算梯度图的Sobel算子的尺寸
• k - 用于计算角点响应函数的参数k，取值范围常在0.04~0.06之间

3.1 代码示例

利用Anaconda搭建OpenCV环境，运行以下代码（Python）：

# -*- coding: utf-8 -*-
import cv2 as cv
from matplotlib import pyplot as plt
import numpy as np

# detector parameters
block_size = 3
sobel_size = 3
k = 0.06

image = cv.imread('building_SDU.jpg')

print(image.shape)
height = image.shape[0]
width = image.shape[1]
channels = image.shape[2]
print("width: %s  height: %s  channels: %s" % (width, height, channels))

gray_img = cv.cvtColor(image, cv.COLOR_BGR2GRAY)

# modify the data type setting to 32-bit floating point
gray_img = np.float32(gray_img)

# detect the corners with appropriate values as input parameters
corners_img = cv.cornerHarris(gray_img, block_size, sobel_size, k)

# result is dilated for marking the corners, not necessary
kernel = cv.getStructuringElement(cv.MORPH_RECT, (3, 3))
dst = cv.dilate(corners_img, kernel)

# Threshold for an optimal value, marking the corners in Green
# image[corners_img>0.01*corners_img.max()] = [0,0,255]

for r in range(height):
    for c in range(width):
        pix = dst[r, c]
        if pix > 0.05 * dst.max():
            cv.circle(image, (c, r), 5, (0, 0, 255), 0)

image = cv.cvtColor(image, cv.COLOR_BGR2RGB)
plt.imshow(image)
plt.show()

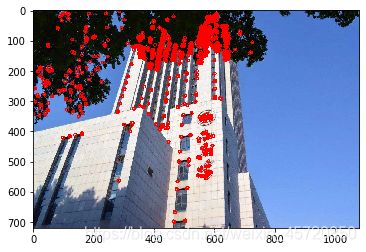
3.2 运行结果

处理前：

处理后：

4 Harris角点的性质

4.1 参数$k$对角点检测的影响

增大$k$的值，将减小角点响应值$R$，降低角点检测的灵敏性，减少被检测角点的数量；减小$k$值，将增大角点响应值$R$，增加角点检测的灵敏性，增加被检测角点的数量。

4.2 Harris角点检测算子光照不变性

在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是阈值的选择，可能会影响角点检测的数量。

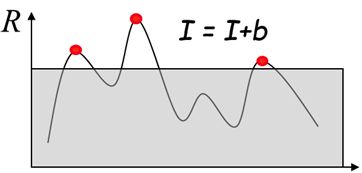
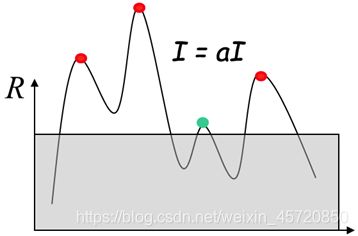
4.3 Harris角点检测算子旋转不变性

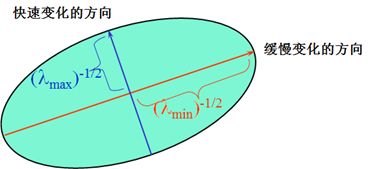
Harris角点检测算子使用的是角点附近的区域灰度二阶矩阵，二阶矩阵可以表示成一个椭圆，椭圆的长短轴是二阶矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值$R$也不发生变化，由此说明Harris角点检测算子具有旋转不变性。

4.4 Harris角点检测算子不具有尺度不变性

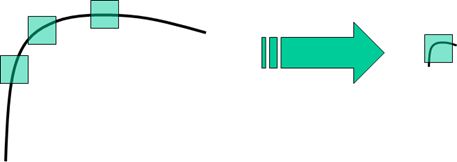
尺度的变化可能将角点变为边缘，或者边缘变为角点，Harris的理论基础并不具有尺度不变性。如下图所示，左侧的图像可能被检测为边缘或曲线，而当左图被缩小时，在检测窗口尺寸不变的前提下，右侧的图像可能被检测为一个角点。

4.5 进一步讨论

上述Harris角点具有光照不变性、旋转不变性、尺度不变性，但是严格意义上来说并不具备仿射不变性。而Harris-Affine是一种新颖的检测仿射不变特征点的方法，可以处理明显的仿射变换，包括大尺度变化和明显的视角变化。

深入了解Harris-Affine角点检测，请移步原论文： Scale & Affine Invariant Interest Point Detectors

5 参考

• Datawhale学习资料
• Harris角点
• Harris角点算法
• 图像特征检测：Harris角点