OpenCv入门

一、Opencv简介

OpenCv简介:OpenCV是应用广泛的开源图像处理库，我们以其为基础，介绍相关的图像处理方法：包括基本的图像处理方法：几何变换，形态学变换，图像平滑，直方图操作，模板匹配，霍夫变换等；特征提取和描述方法：理解角点特征，Harris和Shi-Tomas算法，SIFT/SURF算法，Fast算法，ORB算法等；还有OpenCV在视频操作中的应用，最后的案例是使用OpenCV进行人脸检测。
OpenCV-Python是一个Python绑定库，旨在解决计算机视觉问题。Python是一种由Guido van Rossum开发的通用编程语言，它很快就变得非常流行，主要是因为它的简单性和代码可读性。它使程序员能够用更少的代码行表达思想，而不会降低可读性。与C / C++等语言相比，Python速度较慢。也就是说，Python可以使用C / C++轻松扩展，这使我们可以在C / C++中编写计算密集型代码，并创建可用作Python模块的Python包装器。这给我们带来了两个好处：首先，代码与原始C / C++代码一样快（因为它是在后台工作的实际C++代码），其次，在Python中编写代码比使用C / C++更容易。OpenCV-Python是原始OpenCV C++实现的Python包装器。OpenCV-Python使用Numpy，这是一个高度优化的数据库操作库，具有MATLAB风格的语法。所有OpenCV数组结构都转换为Numpy数组。这也使得与使用Numpy的其他库（如SciPy和Matplotlib）集成更容易。

1.1 图像处理简介

1 图像的起源
1.1 图像是什么
图像是人类视觉的基础，是自然景物的客观反映，是人类认识世界和人类本身的重要源泉。“图”是物体反射或透射光的分布，“像“是人的视觉系统所接受的图在人脑中所形版的印象或认识，照片、绘画、剪贴画、地图、书法作品、手写汉学、传真、卫星云图、影视画面、X光片、脑电图、心电图等都是图像。—姚敏. 数字图像处理：机械工业出版社，2014年。
1.2 模拟图像和数字图像
图像起源于1826年前后法国科学家Joseph Nicéphore Niépce发明的第一张可永久保存的照片，属于模拟图像。模拟图像又称连续图像，它通过某种物理量（如光、电等）的强弱变化来记录图像亮度信息，所以是连续变换的。模拟信号的特点是容易受干扰，如今已经基本全面被数字图像替代。
在第一次世界大战后，1921年美国科学家发明了Bartlane System，并从伦敦传到纽约传输了第一幅数字图像，其亮度用离散数值表示，将图片编码成5个灰度级，如下图所示，通过海底电缆进行传输。在发送端图片被编码并使用打孔带记录，通过系统传输后在接收方使用特殊的打印机恢复成图像。
2 数字图像的表示
2.1 位数
计算机采用0/1编码的系统，数字图像也是利用0/1来记录信息，我们平常接触的图像都是8位数图像，包含0～255灰度，其中0，代表最黑，1，表示最白。
2.2 图像的分类
二值图像：
一幅二值图像的二维矩阵仅由0、1两个值构成，“0”代表黑色，“1”代白色。由于每一像素（矩阵中每一元素）取值仅有0、1两种可能，所以计算机中二值图像的数据类型通常为1个二进制位。二值图像通常用于文字、线条图的扫描识别（OCR）和掩膜图像的存储。

灰度图：
每个像素只有一个采样颜色的图像，这类图像通常显示为从最暗黑色到最亮的白色的灰度，尽管理论上这个采样可以任何颜色的不同深浅，甚至可以是不同亮度上的不同颜色。灰度图像与黑白图像不同，在计算机图像领域中黑白图像只有黑色与白色两种颜色；但是，灰度图像在黑色与白色之间还有许多级的颜色深度。灰度图像经常是在单个电磁波频谱如可见光内测量每个像素的亮度得到的，用于显示的灰度图像通常用每个采样像素8位的非线性尺度来保存，这样可以有256级灰度（如果用16位，则有65536级）。

彩色图：
每个像素通常是由红（R）、绿（G）、蓝（B）三个分量来表示的，分量介于（0，255）。RGB图像与索引图像一样都可以用来表示彩色图像。与索引图像一样，它分别用红（R）、绿（G）、蓝（B）三原色的组合来表示每个像素的颜色。但与索引图像不同的是，RGB图像每一个像素的颜色值（由RGB三原色表示）直接存放在图像矩阵中，由于每一像素的颜色需由R、G、B三个分量来表示，M、N分别表示图像的行列数，三个M x N的二维矩阵分别表示各个像素的R、G、B三个颜色分量。RGB图像的数据类型一般为8位无符号整形，通常用于表示和存放真彩色图像。

1.2 OpenCv的模块

下图列出了OpenCV中包含的各个模块：

其中core、highgui、imgproc是最基础的模块，该课程主要是围绕这几个模块展开的，分别介绍如下：

• core模块实现了最核心的数据结构及其基本运算，如绘图函数、数组操作相关函数等。
• highgui模块实现了视频与图像的读取、显示、存储等接口。
• imgproc模块实现了图像处理的基础方法，包括图像滤波、图像的几何变换、平滑、阈值分割、形态学处理、边缘检测、目标检测、运动分析和对象跟踪等。

对于图像处理其他更高层次的方向及应用，OpenCV也有相关的模块实现

• features2d模块用于提取图像特征以及特征匹配，nonfree模块实现了一些专利算法，如sift特征。
• objdetect模块实现了一些目标检测的功能，经典的基于Haar、LBP特征的人脸检测，基于HOG的行人、汽车等目标检测，分类器使用Cascade
  Classification（级联分类）和Latent SVM等。
• stitching模块实现了图像拼接功能。
• FLANN模块（Fast Library for Approximate Nearest
  Neighbors），包含快速近似最近邻搜索FLANN 和聚类Clustering算法。
• ml模块机器学习模块（SVM，决策树，Boosting等等）。
• photo模块包含图像修复和图像去噪两部分。
• video模块针对视频处理，如背景分离，前景检测、对象跟踪等。
• calib3d模块即Calibration（校准）3D，这个模块主要是相机校准和三维重建相关的内容。包含了基本的多视角几何算法，单个立体摄像头标定，物体姿态估计，立体相似性算法，3D信息的重建等等。
• G-API模块包含超高效的图像处理pipeline引擎

二、OpenCv基本操作

本章主要介绍图像的基础操作，包括：

• 图像的IO操作，读取和保存方法
• 在图像上绘制几何图形
• 怎么获取图像的属性
• 怎么访问图像的像素，进行通道分离，合并等
• 怎么实现颜色空间的变换
• 图像的算术运算

2.1 图像的IO操作(读取，显示，保存)

2.1.1读取图像

cv.imread(要读取的图像，读取图像的方式)

读取方式的标志:

• cv.IMREAD*COLOR：以彩色模式加载图像，任何图像的透明度都将被忽略。这是默认参数。
• cv.IMREAD*GRAYSCALE：以灰度模式加载图像
• cv.IMREAD_UNCHANGED：包括alpha通道的加载图像模式。
  可以使用1、0或者-1来替代上面三个标志

• 参考代码

mport numpy as np
import cv2 as cv
# 以灰度图的形式读取图像
img = cv.imread('messi5.jpg',0)

注意：如果加载的路径有错误，不会报错，会返回一个None值

2.1.2 显示图像

cv.imshow(显示图像的窗口名称，要加载的图像)

注意：在调用显示图像的API后，要调用cv.waitKey()给图像绘制留下时间，否则窗口会出现无响应情况，并且图像无法显示出来。

另外我们也可使用matplotlib对图像进行展示。参考代码如下:

# opencv中显示
cv.imshow('image',img)
cv.waitKey(0)
# matplotlib中展示
plt.imshow(img[:,:,::-1])

2.1.3 保存图像

cv.imwrite(要保存到哪里，要保存的图像)

2.2 绘制几何图形(直线，圆，矩形，添加文字，获取属性)

2.2.1 绘制直线

cv.line(img,start,end,color,thickness)//图片，起点，终点，颜色，宽度

2.2.2 绘制圆

cv.circle(img,centerpoint, r, color, thickness)//图像，圆心，半径，颜色，宽度

2.2.3 绘制矩形

cv.rectangle(img,leftupper,rightdown,color,thickness)//图像，左上角、右下角坐标，颜色，宽度

2.2.4 添加文字

cv.putText(img,text,station, font,fontsize,color,thickness,cv.LINE_AA)//图像，写入的数据、写入的位置，字体，字体大小

2.2.5 获取图像的属性
图像属性包括行数，列数和通道数，图像数据类型，像素数等。

属性	API
形状	img.shape
大小	img.size
类型	img.dtype

2.2.6 图像通道的拆分与合并

有时需要在B，G，R通道图像上单独工作。在这种情况下，需要将BGR图像分割为单个通道。或者在其他情况下，可能需要将这些单独的通道合并到BGR图像。你可以通过以下方式完成。

# 通道拆分
b,g,r = cv.split(img)
# 通道合并
img = cv.merge((b,g,r))

2.2.7 色彩空间的改变

OpenCV中有150多种颜色空间转换方法。最广泛使用的转换方法有两种，BGR↔Gray和BGR↔HSV

cv.cvtColor(input_image，flag)
input_image: 进行颜色空间转换的图像
flag: 转换类型
 - cv.COLOR_BGR2GRAY : BGR↔Gray
 - cv.COLOR_BGR2HSV: BGR→HSV

2.3 算术操作(图像加法、图像混合)

2.3.1 图像的加法
你可以使用OpenCV的cv.add()函数把两幅图像相加，或者可以简单地通过numpy操作添加两个图像，如res = img1 + img2。两个图像应该具有相同的大小和类型，或者第二个图像可以是标量值。
注意：OpenCV加法和Numpy加法之间存在差异。OpenCV的加法是饱和操作，而Numpy添加是模运算。

2.3.2 图像的混合
这其实也是加法，但是不同的是两幅图像的权重不同，这就会给人一种混合或者透明的感觉。图像混合的计算公式如下：

g(x) = (1−α)f0(x) + αf1(x)

通过修改 α 的值（0 → 1），可以实现非常炫酷的混合。函数cv2.addWeighted()可以对图片进行混合操作。

img3 = cv.addWeighted(img1,0.7,img2,0.3,0)

三、OpenCv图像处理

• 图像的几何变换
• 图像的形态学转换
• 图像的平滑方法
• 直方图的方法
• 边缘检测的方法
• 模板匹配和霍夫变换的应用

3.1 几何变换(缩放，平移，旋转，仿射变换，透射变换，金字塔)

3.1.1图像缩放(对图像大小进行调整)

cv2.resize(src,dsize,fx=0,fy=0,interpolation=cv2.INTER_LINEAR)

参数：

• src 要进行操作的图片
• dsize 绝对尺寸，直接指定调整后图像的大小
• fx fy 相对尺寸 dsize设置为0 然后该参数为比例因子
• interpolation：插值方法

插值	含义
cv2.INTER_LINEAR	双线性插值法
cv2.INTER_NEAREST	最近临插值
cv2.INTER_AREA	像素区域重采样（默认）
cv2.INTER_CUBIC	双三次插值

代码示例:

import cv2 as cv
img1=cv.read("1,jpg") #读取图像
#绝对尺寸
rows,cols = img1.shape[:2]
res = cv.resize(img1,(2*cols,2*rows),interpolation=cv.INTER_CUBIC)
#相对尺寸
res1 = cv.resize(img1,None,fx=0.5,fy=0.5)
#使用opencv显示图像
cv.imshow("orignal",img1)
cv.imshow("enlarge",res)
cv.imshow("shrink）",res1)
cv.waitKey(0)
#使用matplotlib显示图像
fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(10,8),dpi=100)
axes[0].imshow(res[:,:,::-1])
axes[0].set_title("绝对尺度（放大）")
axes[1].imshow(img1[:,:,::-1])
axes[1].set_title("原图")
axes[2].imshow(res1[:,:,::-1])
axes[2].set_title("相对尺度（缩小）")
plt.show()

3.1.2 图像平移

cv.warpAffine(img,M,dsize)

参数:

• img: 输图像
• M: 2*3移动矩阵对于(x,y)处的像素点，要把它移动到(x+tx , y+ty)处时，M矩阵应如下设置：
  [ 1 0 tx ]
  [ 0 1 ty ]
  注意：将MM设置为np.float32类型的Numpy数组。
• dsize: 输出图像的大小
  注意：输出图像的大小，它应该是(宽度，高度)的形式。请记住,width=列数，height=行数。

示例:需求是将图像的像素点移动(50,100)的距离：

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
#读取图像
img1=cv.imread('1.jpg')
#平移图像
rows,cols=img1.shape[:2]
M=M=np.float32([1,0.100],[0,1,50]) #平移矩阵
dst=cv.warpAffine(img1,M(cols,rows))
#图像显示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img1[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("平移后结果")
plt.show()

3.1.3 图像旋转
图像旋转是指图像按照某个位置转动一定角度的过程，旋转中图像仍保持这原始尺寸。图像旋转后图像的水平对称轴、垂直对称轴及中心坐标原点都可能会发生变换，因此需要对图像旋转中的坐标进行相应转换。
那图像是怎么进行旋转的呢？如下图所示：

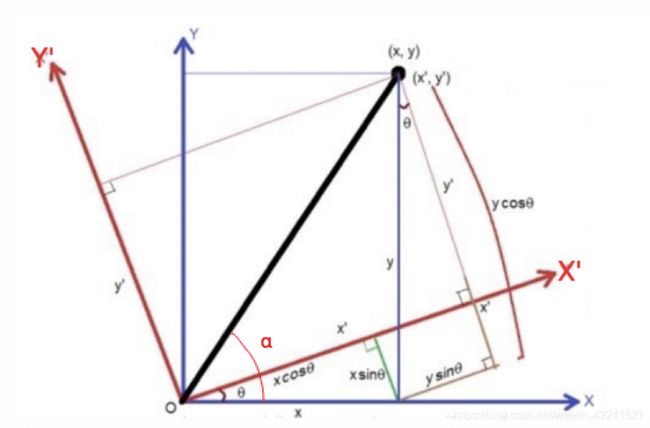
假设图像逆时针旋转\thetaθ，则根据坐标转换可得旋转转换为:

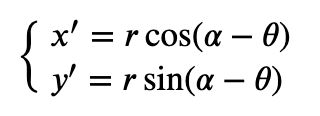
其中：

带入上面的公式中，有：

也可以写成：

同时我们要修正原点的位置，因为原图像中的坐标原点在图像的左上角，经过旋转后图像的大小会有所变化，原点也需要修正。

假设在旋转的时候是以旋转中心为坐标原点的，旋转结束后还需要将坐标原点移到图像左上角，也就是还要进行一次变换。


在OpenCV中图像旋转首先根据旋转角度和旋转中心获取旋转矩阵，然后根据旋转矩阵进行变换，即可实现任意角度和任意中心的旋转效果。

cv2.getRotationMatrix2D(center, angle, scale)#旋转中心，旋转角度，缩放比例

返回：

• M:旋转矩阵 调用cv.warpAffine完成图像的旋转
  示例：

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
#读取图像
img=cv.imread("1.jpg")
# 2 图像旋转
rows,cols = img.shape[:2]
# 2.1 生成旋转矩阵
M = cv.getRotationMatrix2D((cols/2,rows/2),90,1)
# 2.2 进行旋转变换
dst = cv.warpAffine(img,M,(cols,rows))
# 3 图像展示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img1[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("旋转后结果")
plt.show()

3.1.4 仿射变换
图像的仿射变换涉及到图像的形状位置角度的变化，是深度学习预处理中常到的功能,仿射变换主要是对图像的缩放，旋转，翻转和平移等操作的组合。
在OpenCV中，仿射变换的矩阵是一个2×3的矩阵，

其中左边的2×2子矩阵$A$是线性变换矩阵，右边的2×1子矩阵$B$是平移项：

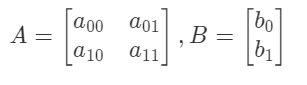
对于图像上的任一位置(x,y)，仿射变换执行的是如下的操作：

需要注意的是，对于图像而言，宽度方向是x，高度方向是y，坐标的顺序和图像像素对应下标一致。所以原点的位置不是左下角而是右上角，y的方向也不是向上，而是向下。

在仿射变换中，原图中所有的平行线在结果图像中同样平行。为了创建这个矩阵我们需要从原图像中找到三个点以及他们在输出图像中的位置。然后cv2.getAffineTransform 会创建一个 2x3 的矩阵，最后这个矩阵会被传给函数 cv2.warpAffine。
示例:

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
#图像读取
img = cv.imread("1.jpg")
# 2 仿射变换
rows,cols = img.shape[:2]
# 2.1 创建变换矩阵
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[100,100],[200,50],[100,250]])
M = cv.getAffineTransform(pts1,pts2)
# 2.2 完成仿射变换
dst = cv.warpAffine(img,M,(cols,rows))
# 3 图像显示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("仿射后结果")
plt.show()

3.1.5 透射变换
透射变换是视角变化的结果，是指利用透视中心、像点、目标点三点共线的条件，按透视旋转定律使承影面（透视面）绕迹线（透视轴）旋转某一角度，破坏原有的投影光线束，仍能保持承影面上投影几何图形不变的变换。

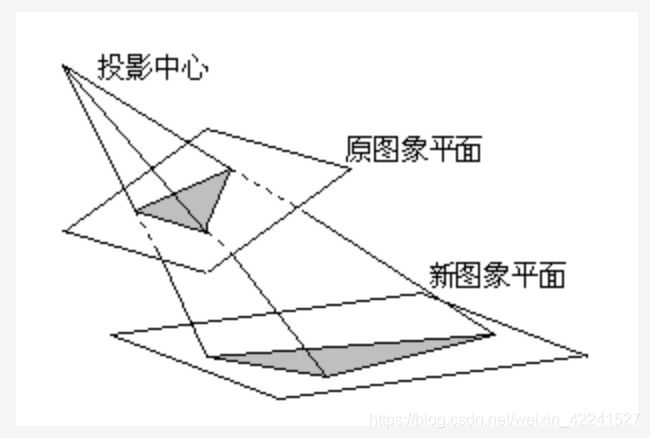
它的本质将图像投影到一个新的视平面，其通用变换公式为：

其中，(u,v)是原始的图像像素坐标，w取值为1，(x=x’/z’,y=y’/z’)是透射变换后的结果。后面的矩阵称为透视变换矩阵，一般情况下，我们将其分为三部分：

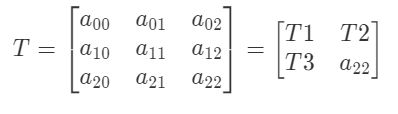
其中：T1表示对图像进行线性变换，T2对图像进行平移，T3表示对图像进行投射变换，a_{22}a
​22
​​ 一般设为1.

在opencv中，我们要找到四个点，其中任意三个不共线，然后获取变换矩阵T，再进行透射变换。通过函数cv.getPerspectiveTransform找到变换矩阵，将cv.warpPerspective应用于此3x3变换矩阵。

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread("./image/image2.jpg")
# 2 透射变换
rows,cols = img.shape[:2]
# 2.1 创建变换矩阵
pts1 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pts2 = np.float32([[100,145],[300,100],[80,290],[310,300]])
T = cv.getPerspectiveTransform(pts1,pts2)
# 2.2 进行变换
dst = cv.warpPerspective(img,T,(cols,rows))
# 3 图像显示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("透射后结果")
plt.show()

3.1.6 图像金字塔
图像金字塔是图像多尺度表达的一种，最主要用于图像的分割，是一种以多分辨率来解释图像的有效但概念简单的结构。
图像金字塔用于机器视觉和图像压缩，一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低，且来源于同一张原始图的图像集合。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。
金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似，层级越高，图像越小，分辨率越低。

cv.pyrUp(img)       #对图像进行上采样
cv.pyrDown(img)        #对图像进行下采样

示例如下:

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 图像读取
img = cv.imread("./image/image2.jpg")
# 进行图像采样
up_img = cv.pyrUp(img)  # 上采样操作
img_1 = cv.pyrDown(img)  # 下采样操作
# 图像显示
cv.imshow('enlarge', up_img)
cv.imshow('original', img)
cv.imshow('shrink', img_1)
cv.waitKey(0)
cv.destroyAllWindows()

3.2 形态学操作（腐蚀，膨胀，开闭运算，礼帽和黑帽）

3.2.1 连通性
在图像中，最小的单位是像素，每个像素周围有8个邻接像素，常见的邻接关系有3种：4邻接、8邻接和D邻接。分别如下图所示：

• 4邻接：像素p(x,y)的4邻域是：(x+1,y)；(x-1,y)；(x,y+1)；(x,y-1)，用N4§表示像素p的4邻接
• D邻接：像素p(x,y)的D邻域是：对角上的点(x+1,y+1)；(x+1,y-1)；(x-1,y+1)；(x-1,y-1)，用ND§ ​​ 表示像素p的D邻域
• 8邻接：像素p(x,y)的8邻域是： 4邻域的点 ＋ D邻域的点，用N8§表示像素p的8邻域

连通性是描述区域和边界的重要概念，两个像素连通的两个必要条件是：
1. 两个像素的位置是否相邻
2.两个像素的灰度值是否满足特定的相 似性准则（或者是否相等
根据连通性的定义，有4联通、8联通和m联通三种。

• 4联通：对于具有值VV的像素p和q，如果q在集合N4§)中，则称这两个像素是4连通。
• 8联通：对于具有值VV的像素p和q，如果q在集 合N8§中，则称这两个像素是8连通。
  
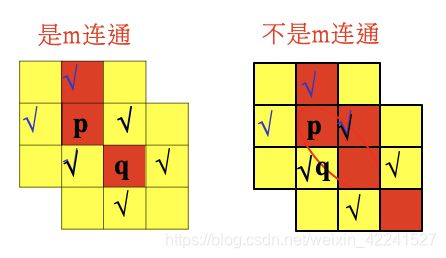
• 对于具有值V的像素pp和qq，如果:
  q在集合N4( p )中，或
  q在集合ND( p)中，并且N4( p)与N4( q)的交集为空（没有值V的像素）
  则称这两个像素是m连通的，即4连通和D连通的混合连通。
  
  3.2.2 形态学操作
  形态学转换是基于图像形状的一些简单操作。它通常在二进制图像上执行。腐蚀和膨胀是两个基本的形态学运算符。然后它的变体形式如开运算，闭运算，礼帽黑帽等。
  腐蚀和膨胀
  腐蚀和膨胀是最基本的形态学操作，腐蚀和膨胀都是针对白色部分（高亮部分）而言的。
  膨胀就是使图像中高亮部分扩张，效果图拥有比原图更大的高亮区域；腐蚀是原图中的高亮区域被蚕食，效果图拥有比原图更小的高亮区域。膨胀是求局部最大值的操作，腐蚀是求局部最小值的操作。
• 腐蚀
  具体操作是：用一个结构元素扫描图像中的每一个像素，用结构元素中的每一个像素与其覆盖的像素做“与”操作，如果都为1，则该像素为1，否则为0。如下图所示，结构A被结构B腐蚀后：
  
  腐蚀的作用是消除物体边界点，使目标缩小，可以消除小于结构元素的噪声点。

 cv.erode(img,kernel,iterations)#处理的图像，核结构，腐蚀的次数（默认1）

• 膨胀
  具体操作是：用一个结构元素扫描图像中的每一个像素，用结构元素中的每一个像素与其覆盖的像素做“与”操作，如果都为0，则该像素为0，否则为1。如下图所示，结构A被结构B腐蚀后：
  

cv.dilate(img,kernel,iterations) #与腐蚀相同的

示例 :使用一个5*5的卷积核实现腐蚀和膨胀的运算：

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread("./image/image3.png")
# 2 创建核结构
kernel = np.ones((5, 5), np.uint8)

# 3 图像腐蚀和膨胀
erosion = cv.erode(img, kernel) # 腐蚀
dilate = cv.dilate(img,kernel) # 膨胀

# 4 图像展示
fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(10,8),dpi=100)
axes[0].imshow(img)
axes[0].set_title("原图")
axes[1].imshow(erosion)
axes[1].set_title("腐蚀后结果")
axes[2].imshow(dilate)
axes[2].set_title("膨胀后结果")
plt.show()

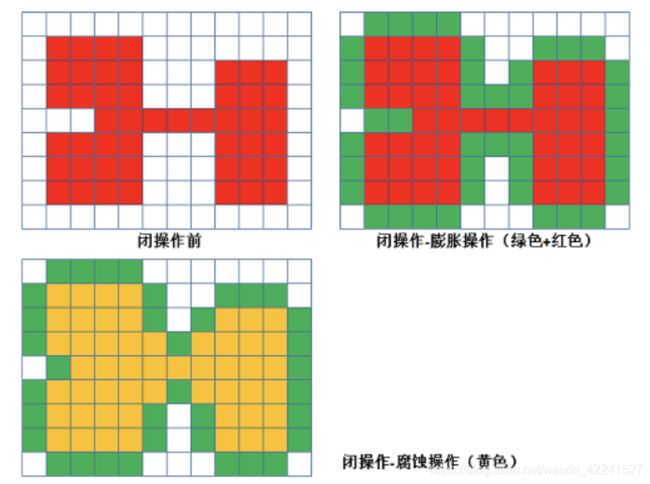
3.2.3 开闭运算
开运算和闭运算是将腐蚀和膨胀按照一定的次序进行处理。 但这两者并不是可逆的，即先开后闭并不能得到原来的图像。

• 开运算
  开运算是先腐蚀后膨胀，其作用是：分离物体，消除小区域。特点：消除噪点，去除小的干扰块，而不影响原来的图像。
  
• 闭运算
  闭运算与开运算相反，是先膨胀后腐蚀，作用是消除/“闭合”物体里面的孔洞，特点：可以填充闭合区域。

cv.morphologyEx(img, op, kernel)#要处理的图像，处理方式（cv.MORPH_OPEN=开，cv.MORPH_CLOSE=闭），核结构

实例:使用10*10的核结构对卷积进行开闭运算的实现。

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img1 = cv.imread("./image/image5.png")
img2 = cv.imread("./image/image6.png")
# 2 创建核结构
kernel = np.ones((10, 10), np.uint8)
# 3 图像的开闭运算
cvOpen = cv.morphologyEx(img1,cv.MORPH_OPEN,kernel) # 开运算
cvClose = cv.morphologyEx(img2,cv.MORPH_CLOSE,kernel)# 闭运算
# 4 图像展示
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,8))
axes[0,0].imshow(img1)
axes[0,0].set_title("原图")
axes[0,1].imshow(cvOpen)
axes[0,1].set_title("开运算结果")
axes[1,0].imshow(img2)
axes[1,0].set_title("原图")
axes[1,1].imshow(cvClose)
axes[1,1].set_title("闭运算结果")
plt.show()

3.2.4 礼帽和黑帽

• 礼帽运算
  原图像与“开运算“的结果图之差，如下式计算：

dst=tophat(src,element)=src-open(src,element)

因为开运算带来的结果是放大了裂缝或者局部低亮度的区域，因此，从原图中减去开运算后的图，得到的效果图突出了比原图轮廓周围的区域更明亮的区域，且这一操作和选择的核的大小相关。
礼帽运算用来分离比邻近点亮一些的斑块。当一幅图像具有大幅的背景的时候，而微小物品比较有规律的情况下，可以使用顶帽运算进行背景提取。

• 黑帽运算
  为”闭运算“的结果图与原图像之差。数学表达式为：

dst=blackhat(src,element)=close(src,element)-src

黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域，且这一操作和选择的核的大小相关。

黑帽运算用来分离比邻近点暗一些的斑块。

cv.morphologyEx(img, op, kernel)

op:处理方式

参数	功能
cv.MORPH_CLOSE	闭运算
cv.MORPH_OPEN	开运算
cv.MORPH_TOPHAT	礼帽运算
cv.MORPH_BLACKHAT	黑帽运算

3.3 图像平滑（均值滤波，高斯滤波，中值滤波）

3.3.1 图像噪声
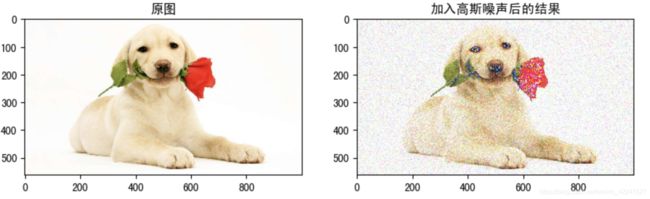
由于图像采集、处理、传输等过程不可避免的会受到噪声的污染，妨碍人们对图像理解及分析处理。常见的图像噪声有高斯噪声、椒盐噪声等。

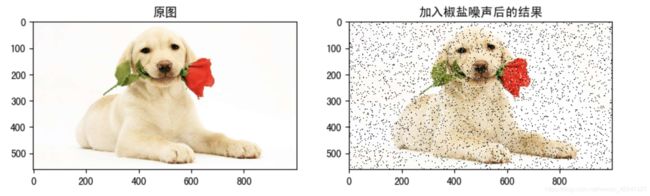
• 椒盐噪声
  椒盐噪声也称为脉冲噪声，是图像中经常见到的一种噪声，它是一种随机出现的白点或者黑点，可能是亮的区域有黑色像素或是在暗的区域有白色像素（或是两者皆有）。椒盐噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。例如失效的感应器导致像素值为最小值，饱和的感应器导致像素值为最大值。
  
• 高斯噪声
  高斯噪声是指噪声密度函数服从高斯分布的一类噪声。由于高斯噪声在空间和频域中数学上的易处理性，这种噪声(也称为正态噪声)模型经常被用于实践中。高斯随机变量z的概率密度函数由下式给出：
  
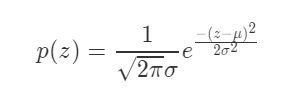
  其中z表示灰度值，μ表示z的平均值或期望值，σ表示z的标准差。标准差的平方sigma^2称为z的方差。高斯函数的曲线如图所示。
  
  
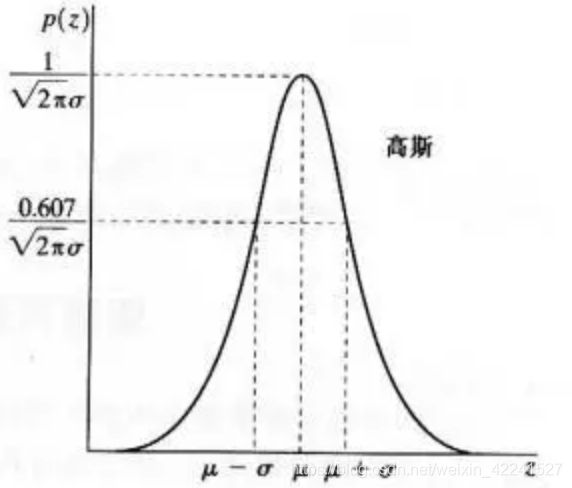
  3.3.2 图像平滑简介
  图像平滑从信号处理的角度看就是去除其中的高频信息，保留低频信息。因此我们可以对图像实施低通滤波。低通滤波可以去除图像中的噪声，对图像进行平滑。
  根据滤波器的不同可分为均值滤波，高斯滤波，中值滤波， 双边滤波。
• 均值滤波

cv.blur(src, ksize, anchor, borderType)#输入图像，卷积核的大小。核中心（默认（-1，-1）），边界类型

示例代码:

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/dogsp.jpeg')
# 2 均值滤波
blur = cv.blur(img,(5,5))
# 3 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('均值滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()

• 高斯滤波
  二维高斯是构建高斯滤波器的基础，其概率分布函数如下所示：
  
  
  
  
  更远的点以此类推。

为了计算权重矩阵，需要设定σ的值。假定σ=1.5，则模糊半径为1的权重矩阵如下：

这9个点的权重总和等于0.4787147，如果只计算这9个点的加权平均，还必须让它们的权重之和等于1，因此上面9个值还要分别除以0.4787147，得到最终的权重矩阵。
计算高斯模糊，有了权重矩阵，就可以计算高斯模糊的值了。
假设现有9个像素点，灰度值（0-255）如下：

每个点乘以对应的权重值：

得到

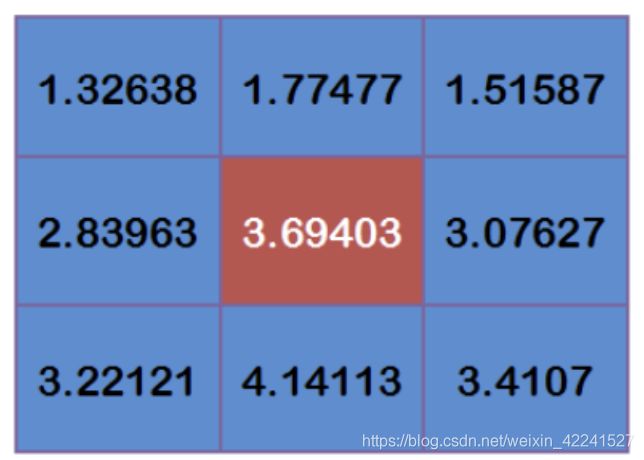
将这9个值加起来，就是中心点的高斯模糊的值。
对所有点重复这个过程，就得到了高斯模糊后的图像。如果原图是彩色图片，可以对RGB三个通道分别做高斯平滑。

cv2.GaussianBlur(src,ksize,sigmaX,sigmay,borderType)

参数:

• src: 输入图像
• ksize:高斯卷积核的大小，注意 ： 卷积核的宽度和高度都应为奇数，且可以不同
• sigmaX: 水平方向的标准差
• sigmaY: 垂直方向的标准差，默认值为0，表示与sigmaX相同
• borderType:填充边界类型
  示例:

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/dogGasuss.jpeg')
# 2 高斯滤波
blur = cv.GaussianBlur(img,(3,3),1)
# 3 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('高斯滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()

• 中值滤波
  中值滤波是一种典型的非线性滤波技术，基本思想是用像素点邻域灰度值的中值来代替该像素点的灰度值。
  中值滤波对椒盐噪声（salt-and-pepper noise）来说尤其有用，因为它不依赖于邻域内那些与典型值差别很大的值。

cv.medianBlur(src, ksize )#输入图像，卷积核的大小

示例:

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/dogsp.jpeg')
# 2 中值滤波
blur = cv.medianBlur(img,5)
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img[:,:,::-1]),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur[:,:,::-1]),plt.title('中值滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()

3.4 直方图

3.4.1 灰度直方图
原理:直方图是对数据进行统计的一种方法，并且将统计值组织到一系列实现定义好的 bin 当中。其中， bin 为直方图中经常用到的一个概念，可以译为 “直条” 或 “组距”，其数值是从数据中计算出的特征统计量，这些数据可以是诸如梯度、方向、色彩或任何其他特征。
 图像直方图（Image Histogram）是用以表示数字图像中亮度分布的直方图，标绘了图像中每个亮度值的像素个数。这种直方图中，横坐标的左侧为较暗的区域，而右侧为较亮的区域。因此一张较暗图片的直方图中的数据多集中于左侧和中间部分，而整体明亮、只有少量阴影的图像则相反。

注意：直方图是根据灰度图进行绘制的，而不是彩色图像。   假设有一张图像的信息（灰度值 0 - 255，已知数字的范围包含 256 个值，于是可以按一定规律将这个范围分割成子区域（也就是 bins）。
如:
然后再统计每一个 bin(i) 的像素数目。可以得到下图（其中 x 轴表示 bin，y 轴表示各个 bin 中的像素个数）：  

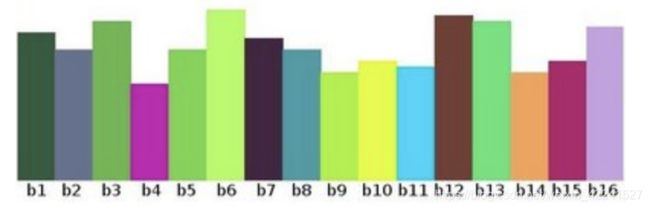
直方图的一些术语和细节：

• dims：需要统计的特征数目。在上例中，dims = 1 ，因为仅仅统计了灰度值。
• bins：每个特征空间子区段的数目，可译为 “直条” 或 “组距”，在上例中， bins = 16。
• range：要统计特征的取值范围。在上例中，range = [0, 255]。

直方图的意义：

• 直方图是图像中像素强度分布的图形表达方式。
• 它统计了每一个强度值所具有的像素个数。
• 不同的图像的直方图可能是相同的

3.4.2 直方图的计算和绘制
我们使用OpenCV中的方法统计直方图，并使用matplotlib将其绘制出来。

cv2.calcHist(images,channels,mask,histSize,ranges[,hist[,accumulate]])

参数:

• images: 原图像。当传入函数时应该用中括号 [] 括起来，例如：[img]。
• channels: 如果输入图像是灰度图，它的值就是 [0]；如果是彩色图像的话，传入的参数可以是 [0]，[1]，[2] 它们分别对应着通道 B，G，R。
• mask: 掩模图像。要统计整幅图像的直方图就把它设为 None。但是如果你想统计图像某一部分的直方图的话，你就需要制作一个掩模图像，并使用它。（后边有例子）
• histSize:BIN 的数目。也应该用中括号括起来，例如：[256]。
• ranges: 像素值范围，通常为 [0，256]

示例：如下图，绘制相应的直方图

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
# 1 直接以灰度图的方式读入
img = cv.imread('./image/cat.jpeg',0)
# 2 统计灰度图
histr = cv.calcHist([img],[0],None,[256],[0,256])
# 3 绘制灰度图
plt.figure(figsize=(10,6),dpi=100)
plt.plot(histr)
plt.grid()
plt.show()

3.4.3 掩膜的应用
掩膜是用选定的图像、图形或物体，对要处理的图像进行遮挡，来控制图像处理的区域。
在数字图像处理中，我们通常使用二维矩阵数组进行掩膜。掩膜是由0和1组成一个二进制图像，利用该掩膜图像要处理的图像进行掩膜，其中1值的区域被处理，0 值区域被屏蔽，不会处理。
掩膜的主要用途是：

• 提取感兴趣区域：用预先制作的感兴趣区掩模与待处理图像进行”与“操作，得到感兴趣区图像，感兴趣区内图像值保持不变，而区外图像值都为0。
• 屏蔽作用：用掩模对图像上某些区域作屏蔽，使其不参加处理或不参加处理参数的计算，或仅对屏蔽区作处理或统计。
• 结构特征提取：用相似性变量或图像匹配方法检测和提取图像中与掩模相似的结构特征。
• 特殊形状图像制作

掩膜在遥感影像处理中使用较多，当提取道路或者河流，或者房屋时，通过一个掩膜矩阵来对图像进行像素过滤，然后将我们需要的地物或者标志突出显示出来。
我们使用cv.calcHist（）来查找完整图像的直方图。 如果要查找图像某些区域的直方图，该怎么办？ 只需在要查找直方图的区域上创建一个白色的掩膜图像，否则创建黑色， 然后将其作为掩码mask传递即可。
示例:

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
# 1. 直接以灰度图的方式读入
img = cv.imread('./image/cat.jpeg',0)
# 2. 创建蒙版
mask = np.zeros(img.shape[:2], np.uint8)
mask[400:650, 200:500] = 255
# 3.掩模
masked_img = cv.bitwise_and(img,img,mask = mask)
# 4. 统计掩膜后图像的灰度图
mask_histr = cv.calcHist([img],[0],mask,[256],[1,256])
# 5. 图像展示
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,8))
axes[0,0].imshow(img,cmap=plt.cm.gray)
axes[0,0].set_title("原图")
axes[0,1].imshow(mask,cmap=plt.cm.gray)
axes[0,1].set_title("蒙版数据")
axes[1,0].imshow(masked_img,cmap=plt.cm.gray)
axes[1,0].set_title("掩膜后数据")
axes[1,1].plot(mask_histr)
axes[1,1].grid()
axes[1,1].set_title("灰度直方图")
plt.show()

3.4.4 直方图均衡化
原理与应用
想象一下，如果一副图像中的大多数像素点的像素值都集中在某一个小的灰度值值范围之内会怎样呢？如果一幅图像整体很亮，那所有的像素值的取值个数应该都会很高。所以应该把它的直方图做一个横向拉伸（如下图），就可以扩大图像像素值的分布范围，提高图像的对比度，这就是直方图均衡化要做的事情。

“直方图均衡化”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在更广泛灰度范围内的分布。直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。
这种方法提高图像整体的对比度，特别是有用数据的像素值分布比较接近时，在X光图像中使用广泛，可以提高骨架结构的显示，另外在曝光过度或不足的图像中可以更好的突出细节。
使用opencv进行直方图统计时，使用的是：

dst = cv.equalizeHist(img)#img:灰度图像   dst:均衡化后的结果

示例

import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
# 1. 直接以灰度图的方式读入
img = cv.imread('./image/cat.jpeg',0)
# 2. 均衡化处理
dst = cv.equalizeHist(img)
# 3. 结果展示
fig,axes=plt.subplots(nrows=2,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img,cmap=plt.cm.gray)
axes[0].set_title("原图")
axes[1].imshow(dst,cmap=plt.cm.gray)
axes[1].set_title("均衡化后结果")
plt.show()

3.4.5 自适应的直方图均衡化
上述的直方图均衡，我们考虑的是图像的全局对比度。 的确在进行完直方图均衡化之后，图片背景的对比度被改变了，在猫腿这里太暗，我们丢失了很多信息，所以在许多情况下，这样做的效果并不好。如下图所示，对比下两幅图像中雕像的画面，由于太亮我们丢失了很多信息。

为了解决这个问题， 需要使用自适应的直方图均衡化。 此时， 整幅图像会被分成很多小块，这些小块被称为“tiles”（在 OpenCV 中 tiles 的 大小默认是 8x8），然后再对每一个小块分别进行直方图均衡化。 所以在每一个的区域中， 直方图会集中在某一个小的区域中）。如果有噪声的话，噪声会被放大。为了避免这种情况的出现要使用对比度限制。对于每个小块来说，如果直方图中的 bin 超过对比度的上限的话，就把 其中的像素点均匀分散到其他 bins 中，然后在进行直方图均衡化。

最后，为了 去除每一个小块之间的边界，再使用双线性差值，对每一小块进行拼接。

cv.createCLAHE(clipLimit, tileGridSize) #对比度限制（默认40），分块的大小（默认8*8）

import numpy as np
import cv2 as cv
# 1. 以灰度图形式读取图像
img = cv.imread('./image/cat.jpeg',0)
# 2. 创建一个自适应均衡化的对象，并应用于图像
clahe = cv.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
cl1 = clahe.apply(img)
# 3. 图像展示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img,cmap=plt.cm.gray)
axes[0].set_title("原图")
axes[1].imshow(cl1,cmap=plt.cm.gray)
axes[1].set_title("自适应均衡化后的结果")
plt.show()

3.5 边缘检测(Sobel算子，Scharr算子和拉普拉斯算子)

3.5.1 原理
边缘检测是图像处理和计算机视觉中的基本问题，边缘检测的目的是标识数字图像中亮度变化明显的点。图像属性中的显著变化通常反映了属性的重要事件和变化。边缘的表现形式如下图所示：

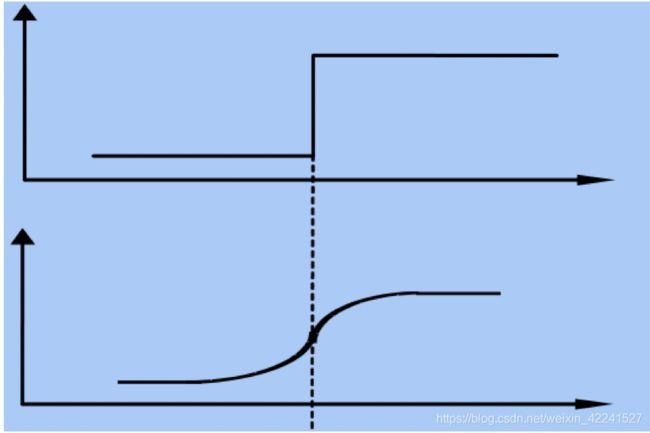
图像边缘检测大幅度地减少了数据量，并且剔除了可以认为不相关的信息，保留了图像重要的结构属性。有许多方法用于边缘检测，它们的绝大部分可以划分为两类：基于搜索和基于零穿越。

• 基于搜索：通过寻找图像一阶导数中的最大值来检测边界，然后利用计算结果估计边缘的局部方向，通常采用梯度的方向，并利用此方向找到局部梯度模的最大值，代表算法是Sobel算子和Scharr算子。
  
• 基于零穿越：通过寻找图像二阶导数零穿越来寻找边界，代表算法是Laplacian算子。
  

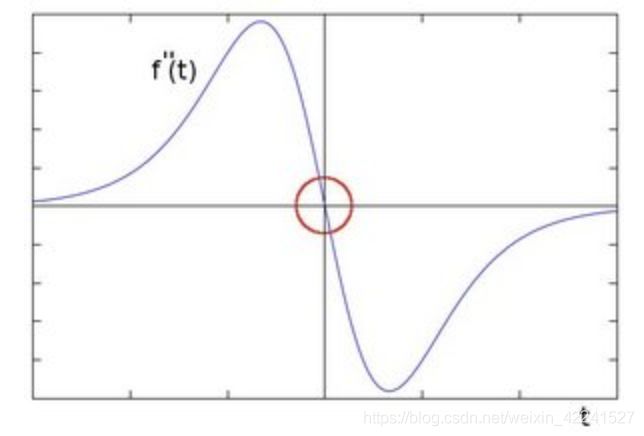
3.5.2 Sobel检测算子
Sobel边缘检测算法比较简单，实际应用中效率比canny边缘检测效率要高，但是边缘不如Canny检测的准确，但是很多实际应用的场合，sobel边缘却是首选，Sobel算子是高斯平滑与微分操作的结合体，所以其抗噪声能力很强，用途较多。尤其是效率要求较高，而对细纹理不太关心的时候。

注意:当内核大小为3时, 以上Sobel内核可能产生比较明显的误差， 为解决这一问题，我们使用Scharr函数，但该函数仅作用于大小为3的内核。该函数的运算与Sobel函数一样快，但结果却更加精确，其计算方法为:

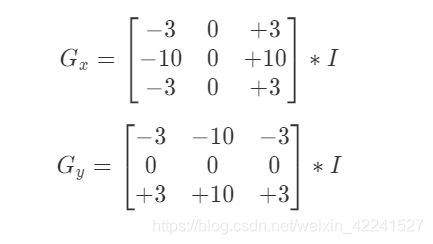
Sobel_x_or_y = cv2.Sobel(src, ddepth, dx, dy, dst, ksize, scale, delta, borderType)

参数:

• src：传入的图像
• ddepth: 图像的深度
• dx和dy: 指求导的阶数，0表示这个方向上没有求导，取值为0、1。
• ksize: 是Sobel算子的大小，即卷积核的大小，必须为奇数1、3、5、7，默认为3。注意：如果ksize=-1，就演变成为3x3的Scharr算子。
• scale：缩放导数的比例常数，默认情况为没有伸缩系数。
• borderType：图像边界的模式，默认值为cv2.BORDER_DEFAULT。

Sobel函数求完导数后会有负值，还有会大于255的值。而原图像是uint8，即8位无符号数，所以Sobel建立的图像位数不够，会有截断。因此要使用16位有符号的数据类型，即cv2.CV_16S。处理完图像后，再使用cv2.convertScaleAbs()函数将其转回原来的uint8格式，否则图像无法显示。
Sobel算子是在两个方向计算的，最后还需要用cv2.addWeighted( )函数将其组合起来

Scale_abs = cv2.convertScaleAbs(x)  # 格式转换函数
result = cv2.addWeighted(src1, alpha, src2, beta) # 图像混合

示例：

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 读取图像
img = cv.imread('./image/horse.jpg',0)
# 2 计算Sobel卷积结果
x = cv.Sobel(img, cv.CV_16S, 1, 0)
y = cv.Sobel(img, cv.CV_16S, 0, 1)
# 3 将数据进行转换
Scale_absX = cv.convertScaleAbs(x)  # convert 转换  scale 缩放
Scale_absY = cv.convertScaleAbs(y)
# 4 结果合成
result = cv.addWeighted(Scale_absX, 0.5, Scale_absY, 0.5, 0)
# 5 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(result,cmap = plt.cm.gray),plt.title('Sobel滤波后结果')
plt.xticks([]), plt.yticks([])
plt.show()

将上述代码中计算sobel算子的部分中将ksize设为-1，就是利用Scharr进行边缘检测。

x = cv.Sobel(img, cv.CV_16S, 1, 0, ksize = -1)
y = cv.Sobel(img, cv.CV_16S, 0, 1, ksize = -1)

3.5.3 Laplacian算子

laplacian = cv2.Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])

参数:

• Src: 需要处理的图像，
• Ddepth: 图像的深度，-1表示采用的是原图像相同的深度，目标图像的深度必须大于等于原图像的深度；
• ksize：算子的大小，即卷积核的大小，必须为1,3,5,7。

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 读取图像
img = cv.imread('./image/horse.jpg',0)
# 2 laplacian转换
result = cv.Laplacian(img,cv.CV_16S)
Scale_abs = cv.convertScaleAbs(result)
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(Scale_abs,cmap = plt.cm.gray),plt.title('Laplacian检测后结果')
plt.xticks([]), plt.yticks([])
plt.show()

3.5.4 Canny边缘检测
Canny 边缘检测算法是一种非常流行的边缘检测算法，是 John F. Canny 于 1986年提出的，被认为是最优的边缘检测算法。
Canny边缘检测算法是由4步构成，分别介绍如下：

• 第一步：噪声去除
  由于边缘检测很容易受到噪声的影响，所以首先使用$5\ast 5$高斯滤波器去除噪声，在图像平滑那一章节中已经介绍过

• 第二步：计算图像梯度
  对平滑后的图像使用 Sobel 算子计算水平方向和竖直方向的一阶导数（Gx 和 Gy）。根据得到的这两幅梯度图（Gx 和 Gy）找到边界的梯度和方向，公式如下:
  
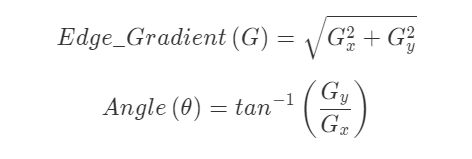
  如果某个像素点是边缘，则其梯度方向总是垂直与边缘垂直。梯度方向被归为四类：垂直，水平，和两个对角线方向。

• 第三步：非极大值抑制
  在获得梯度的方向和大小之后，对整幅图像进行扫描，去除那些非边界上的点。对每一个像素进行检查，看这个点的梯度是不是周围具有相同梯度方向的点中最大的。如下图所示：
  
  A点位于图像的边缘，在其梯度变化方向，选择像素点B和C，用来检验A点的梯度是否为极大值，若为极大值，则进行保留，否则A点被抑制，最终的结果是具有“细边”的二进制图像。

• 第四步：滞后阈值
  现在要确定真正的边界。 我们设置两个阈值： minVal 和 maxVal。 当图像的灰度梯度高于 maxVal 时被认为是真的边界， 低于 minVal 的边界会被抛弃。如果介于两者之间的话，就要看这个点是否与某个被确定为真正的边界点相连，如果是就认为它也是边界点，如果不是就抛弃。如下图：
  

canny = cv2.Canny(image, threshold1, threshold2)

• image:灰度图，
• threshold1: minval，较小的阈值将间断的边缘连接起来
• threshold2: maxval，较大的阈值检测图像中明显的边缘

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像读取
img = cv.imread('./image/horse.jpg',0)
# 2 Canny边缘检测
lowThreshold = 0
max_lowThreshold = 100
canny = cv.Canny(img, lowThreshold, max_lowThreshold) 
# 3 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.subplot(121),plt.imshow(img,cmap=plt.cm.gray),plt.title('原图')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(canny,cmap = plt.cm.gray),plt.title('Canny检测后结果')
plt.xticks([]), plt.yticks([])
plt.show()

3.6 模版匹配和霍夫变换

3.6.1 模板匹配
原理:所谓的模板匹配，就是在给定的图片中查找和模板最相似的区域，该算法的输入包括模板和图片，整个任务的思路就是按照滑窗的思路不断的移动模板图片，计算其与图像中对应区域的匹配度，最终将匹配度最高的区域选择为最终的结果。

res = cv.matchTemplate(img,template,method)

参数:

• img: 要进行模板匹配的图像
• Template ：模板
• method：实现模板匹配的算法，主要有：
  ① 平方差匹配(CV_TM_SQDIFF)：利用模板与图像之间的平方差进行匹配，最好的匹配是0，匹配越差，匹配的值越大。
  ②相关匹配(CV_TM_CCORR)：利用模板与图像间的乘法进行匹配，数值越大表示匹配程度较高，越小表示匹配效果差。
  ③利用相关系数匹配(CV_TM_CCOEFF)：利用模板与图像间的相关系数匹配，1表示完美的匹配，-1表示最差的匹配。

完成匹配后，使用cv.minMaxLoc()方法查找最大值所在的位置即可。如果使用平方差作为比较方法，则最小值位置是最佳匹配位置。
示例:

通过matchTemplate实现模板匹配，使用minMaxLoc定位最匹配的区域，并用矩形标注最匹配的区域。

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
# 1 图像和模板读取
img = cv.imread('./image/wulin2.jpeg')
template = cv.imread('./image/wulin.jpeg')
h,w,l = template.shape
# 2 模板匹配
# 2.1 模板匹配
res = cv.matchTemplate(img, template, cv.TM_CCORR)
# 2.2 返回图像中最匹配的位置，确定左上角的坐标，并将匹配位置绘制在图像上
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res)
# 使用平方差时最小值为最佳匹配位置
# top_left = min_loc
top_left = max_loc
bottom_right = (top_left[0] + w, top_left[1] + h)
cv.rectangle(img, top_left, bottom_right, (0,255,0), 2)
# 3 图像显示
plt.imshow(img[:,:,::-1])
plt.title('匹配结果'), plt.xticks([]), plt.yticks([])
plt.show()

拓展：模板匹配不适用于尺度变换，视角变换后的图像，这时我们就要使用关键点匹配算法，比较经典的关键点检测算法包括SIFT和SURF等，主要的思路是首先通过关键点检测算法获取模板和测试图片中的关键点；然后使用关键点匹配算法处理即可，这些关键点可以很好的处理尺度变化、视角变换、旋转变化、光照变化等，具有很好的不变性。

3.6.1霍夫变换
霍夫变换常用来提取图像中的直线和圆等几何形状
霍夫线检测

cv.HoughLines(img, rho, theta, threshold)

参数:

• img: 检测的图像，要求是二值化的图像，所以在调用霍夫变换之前首先要进行二值化，或者进行Canny边缘检测
• rho、theta: p和θ的精确度
• threshold: 阈值，只有累加器中的值高于该阈值时才被认为是直线。
  示例:

import numpy as np
import random
import cv2 as cv
import matplotlib.pyplot as plt
# 1.加载图片，转为二值图
img = cv.imread('./image/rili.jpg')

gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
edges = cv.Canny(gray, 50, 150)

# 2.霍夫直线变换
lines = cv.HoughLines(edges, 0.8, np.pi / 180, 150)
# 3.将检测的线绘制在图像上（注意是极坐标噢）
for line in lines:
    rho, theta = line[0]
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a * rho
    y0 = b * rho
    x1 = int(x0 + 1000 * (-b))
    y1 = int(y0 + 1000 * (a))
    x2 = int(x0 - 1000 * (-b))
    y2 = int(y0 - 1000 * (a))
    cv.line(img, (x1, y1), (x2, y2), (0, 255, 0))
# 4. 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('霍夫变换线检测')
plt.xticks([]), plt.yticks([])
plt.show()

霍夫圆检测:

circles = cv.HoughCircles(image, method, dp, minDist, param1=100, param2=100, minRadius=0,maxRadius=0 )

参数:

• image：输入图像，应输入灰度图像
• method：使用霍夫变换圆检测的算法，它的参数是CV_HOUGH_GRADIENT
• dp：霍夫空间的分辨率，dp=1时表示霍夫空间与输入图像空间的大小一致，dp=2时霍夫空间是输入图像空间的一半，以此类推
• minDist为圆心之间的最小距离，如果检测到的两个圆心之间距离小于该值，则认为它们是同一个圆心
• param1：边缘检测时使用Canny算子的高阈值，低阈值是高阈值的一半。
• param2：检测圆心和确定半径时所共有的阈值
• minRadius和maxRadius为所检测到的圆半径的最小值和最大值

返回:

• circles：输出圆向量，包括三个浮点型的元素——圆心横坐标，圆心纵坐标和圆半径

示例:
由于霍夫圆检测对噪声比较敏感，所以首先对图像进行中值滤波。

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
# 1 读取图像，并转换为灰度图
planets = cv.imread("./image/star.jpeg")
gay_img = cv.cvtColor(planets, cv.COLOR_BGRA2GRAY)
# 2 进行中值模糊，去噪点
img = cv.medianBlur(gay_img, 7)  
# 3 霍夫圆检测
circles = cv.HoughCircles(img, cv.HOUGH_GRADIENT, 1, 200, param1=100, param2=30, minRadius=0, maxRadius=100)
# 4 将检测结果绘制在图像上
for i in circles[0, :]:  # 遍历矩阵每一行的数据
    # 绘制圆形
    cv.circle(planets, (i[0], i[1]), i[2], (0, 255, 0), 2)
    # 绘制圆心
    cv.circle(planets, (i[0], i[1]), 2, (0, 0, 255), 3)
# 5 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(planets[:,:,::-1]),plt.title('霍夫变换圆检测')
plt.xticks([]), plt.yticks([])
plt.show()

四、图像特征提取与描述

4.1 角点特征

图像的特征：
大多数人都玩过拼图游戏。首先拿到完整图像的碎片，然后把这些碎片以正确的方式排列起来从而重建这幅图像。如果把拼图游戏的原理写成计算机程序，那计算机就也会玩拼图游戏了。
大多数人都玩过拼图游戏。首先拿到完整图像的碎片，然后把这些碎片以正确的方式排列起来从而重建这幅图像。如果把拼图游戏的原理写成计算机程序，那计算机就也会玩拼图游戏了。

如上图所示，蓝色框中的区域是一个平面很难被找到和跟踪。无论向哪个方向移动蓝色框，都是一样的。对于黑色框中的区域，它是一个边缘。如果沿垂直方向移动，它会改变。但是如果沿水平方向移动就不会改变。而红色框中的角点，无论你向那个方向移动，得到的结果都不同，这说明它是唯一的。 所以，我们说角点是一个好的图像特征，也就回答了前面的问题。

角点是图像很重要的特征,对图像图形的理解和分析有很重要的作用。角点在三维场景重建运动估计，目标跟踪、目标识别、图像配准与匹配等计算机视觉领域起着非常重要的作用。在现实世界中，角点对应于物体的拐角，道路的十字路口、丁字路口等

那我们怎样找到这些角点呢？接下来我们使用 OpenCV 中的各种算法来查找图像的特征，并对它们进行描述。

4.2 Harris和Shi-Tomas算法

4.2.1 Harris角点检测
Harris角点检测的思想是通过图像的局部的小窗口观察图像，角点的特征是窗口沿任意方向移动都会导致图像灰度的明显变化，如下图所示：

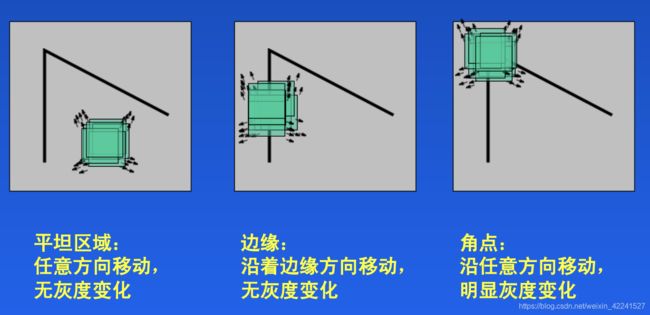
dst=cv.cornerHarris(src, blockSize, ksize, k)

参数:

• img：数据类型为 float32 的输入图像。
• blockSize：角点检测中要考虑的邻域大小。
• ksize：sobel求导使用的核大小
• 角点检测方程中的自由参数，取值参数为 [0.04，0.06].

示例：

import cv2 as cv
import numpy as np 
import matplotlib.pyplot as plt
# 1 读取图像，并转换成灰度图像
img = cv.imread('./image/chessboard.jpg')
gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
# 2 角点检测
# 2.1 输入图像必须是 float32
gray = np.float32(gray)

# 2.2 最后一个参数在 0.04 到 0.05 之间
dst = cv.cornerHarris(gray,2,3,0.04)
# 3 设置阈值，将角点绘制出来，阈值根据图像进行选择
img[dst>0.001*dst.max()] = [0,0,255]
# 4 图像显示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('Harris角点检测')
plt.xticks([]), plt.yticks([])
plt.show()

Harris角点检测的优缺点：
优点:

• 旋转不变性，椭圆转过一定角度但是其形状保持不变（特征值保持不变）
• 对于图像灰度的仿射变化具有部分的不变性，由于仅仅使用了图像的一介导数，对于图像灰度平移变化不变；对于图像灰度尺度变化不变

缺点:

• 对尺度很敏感，不具备几何尺度不变性。
• 提取的角点是像素级的

4.2.2 Shi-Tomasi角点检测
Shi-Tomasi算法是对Harris角点检测算法的改进，一般会比Harris算法得到更好的角点。Harris 算法的角点响应函数是将矩阵 M 的行列式值与 M 的迹相减，利用差值判断是否为角点。后来Shi 和Tomasi 提出改进的方法是，若矩阵M的两个特征值中较小的一个大于阈值，则认为他是角点，即：

从这幅图中，可以看出来只有当 λ1 和 λ 2 都大于最小值时，才被认为是角点。

corners = cv2.goodFeaturesToTrack ( image, maxcorners, qualityLevel, minDistance )

参数:

• Image: 输入灰度图像
• maxCorners : 获取角点数的数目。
• qualityLevel：该参数指出最低可接受的角点质量水平，在0-1之间。
• minDistance：角点之间最小的欧式距离，避免得到相邻特征点。

返回:

• Corners: 搜索到的角点，在这里所有低于质量水平的角点被排除掉，然后把合格的角点按质量排序，然后将质量较好的角点附近（小于最小欧式距离）的角点删掉，最后找到maxCorners个角点返回。

示例：

import numpy as np 
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread('./image/tv.jpg') 
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
# 2 角点检测
corners = cv.goodFeaturesToTrack(gray,1000,0.01,10)  
# 3 绘制角点
for i in corners:
    x,y = i.ravel()
    cv.circle(img,(x,y),2,(0,0,255),-1)
# 4 图像展示
plt.figure(figsize=(10,8),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('shi-tomasi角点检测')
plt.xticks([]), plt.yticks([])
plt.show()

4.3 SIFT/SURF算法

SIFT原理：
前面两节我们介绍了Harris和Shi-Tomasi角点检测算法，这两种算法具有旋转不变性，但不具有尺度不变性，以下图为例，在左侧小图中可以检测到角点，但是图像被放大后，在使用同样的窗口，就检测不到角点了。

所以，下面我们来介绍一种计算机视觉的算法，尺度不变特征转换即SIFT (Scale-invariant feature transform)。它用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量，此算法由 David Lowe在1999年所发表，2004年完善总结。应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对等领域。

SIFT算法的实质是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。
具体实现:

#实例化sift
sift = cv.xfeatures2d.SIFT_create()

利用sift.detectAndCompute()检测关键点并计算
kp,des = sift.detectAndCompute(gray,None)#灰度图像

返回:

• kp: 关键点信息，包括位置，尺度，方向信息
• des: 关键点描述符，每个关键点对应128个梯度信息的特征向量

#将关键点检测结果绘制在图像上
cv.drawKeypoints(image, keypoints, outputimage, color, flags)

参数:

• image: 原始图像
• keypoints：关键点信息，将其绘制在图像上
• outputimage：输出图片，可以是原始图像
• color：颜色设置，通过修改（b,g,r）的值,更改画笔的颜色，b=蓝色，g=绿色，r=红色。
• flags：绘图功能的标识设置
  ①cv2.DRAW_MATCHES_FLAGS_DEFAULT：创建输出图像矩阵，使用现存的输出图像绘制匹配对和特征点，对每一个关键点只绘制中间点。 ②cv2.DRAW_MATCHES_FLAGS_DRAW_OVER_OUTIMG：不创建输出图像矩阵，而是在输出图像上绘制匹配对
  ③cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS：对每一个特征点绘制带大小和方向的关键点图形
  ④cv2.DRAW_MATCHES_FLAGS_NOT_DRAW_SINGLE_POINTS：单点的特征点不被绘制

示例：

利用SIFT算法在中央电视台的图片上检测关键点，并将其绘制出来：

import cv2 as cv 
import numpy as np
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread('./image/tv.jpg')
gray= cv.cvtColor(img,cv.COLOR_BGR2GRAY)
# 2 sift关键点检测
# 2.1 实例化sift对象
sift = cv.xfeatures2d.SIFT_create()

# 2.2 关键点检测：kp关键点信息包括方向，尺度，位置信息，des是关键点的描述符
kp,des=sift.detectAndCompute(gray,None)
# 2.3 在图像上绘制关键点的检测结果
cv.drawKeypoints(img,kp,img,flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
# 3 图像显示
plt.figure(figsize=(8,6),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('sift检测')
plt.xticks([]), plt.yticks([])
plt.show()

五、视频操作

5.1视频读写

5.1.1 从文件中读取视频并播放
在OpenCV中我们要获取一个视频，需要创建一个VideoCapture对象，指定你要读取的视频文件：

1. 创建读取视频的对象

cap = cv.VideoCapture(filepath) #视频文件路径

2. 视频的属性信息

#获取视频的某些属性
retval = cap.get(propId)

参数:propId: 从0到18的数字，每个数字表示视频的属性

常用属性有：

#修改视频的属性信息
cap.set(propId，value) #proid: 属性的索引，与上面的表格相对应   value: 修改后的属性值

#判断图像是否读取成功
isornot = cap.isOpened() #返回true或false

#获取视频的一帧图像
ret, frame = cap.read() 

参数:

• ret: 若获取成功返回True，获取失败，返回False
• Frame: 获取到的某一帧的图像

调用cv.imshow()显示图像，在显示图像时使用cv.waitkey()设置适当的持续时间，如果太低视频会播放的非常快，如果太高就会播放的非常慢，通常情况下我们设置25ms就可以了。
最后，调用cap.realease()将视频释放掉
示例:

import numpy as np
import cv2 as cv
# 1.获取视频对象
cap = cv.VideoCapture('DOG.wmv')
# 2.判断是否读取成功
while(cap.isOpened()):
    # 3.获取每一帧图像
    ret, frame = cap.read()
    # 4. 获取成功显示图像
    if ret == True:
        cv.imshow('frame',frame)
    # 5.每一帧间隔为25ms
    if cv.waitKey(25) & 0xFF == ord('q'):
        break
# 6.释放视频对象
cap.release()
cv.destoryAllwindows()

5.1.2 保存视频
在OpenCV中我们保存视频使用的是VedioWriter对象，在其中指定输出文件的名称，如下所示：

#创建视频写入的对象
out = cv2.VideoWriter(filename,fourcc, fps, frameSize)

参数:

• filename：视频保存的位置
• fourcc：指定视频编解码器的4字节代码
• fps：帧率
• frameSize：帧大小
• 设置视频的编解码器，如下所示，

retval = cv2.VideoWriter_fourcc( c1, c2, c3, c4 )

c1,c2,c3,c4: 是视频编解码器的4字节代码，在fourcc.org中找到可用代码列表，与平台紧密相关，常用的有：在Windows中：DIVX（.avi）在OS中：MJPG（.mp4），DIVX（.avi），X264（.mkv）。
利用cap.read()获取视频中的每一帧图像，并使用out.write()将某一帧图像写入视频中。
使用cap.release()和out.release()释放资源。
示例:

import cv2 as cv
import numpy as np

# 1. 读取视频
cap = cv.VideoCapture("DOG.wmv")

# 2. 获取图像的属性（宽和高，）,并将其转换为整数
frame_width = int(cap.get(3))
frame_height = int(cap.get(4))

# 3. 创建保存视频的对象，设置编码格式，帧率，图像的宽高等
out = cv.VideoWriter('outpy.avi',cv.VideoWriter_fourcc('M','J','P','G'), 10, (frame_width,frame_height))
while(True):
    # 4.获取视频中的每一帧图像
    ret, frame = cap.read()
    if ret == True: 
        # 5.将每一帧图像写入到输出文件中
        out.write(frame)
    else:
        break 

# 6.释放资源
cap.release()
out.release()
cv.destroyAllWindows()

5.2 视频追踪

5.2.1 meanshift
meanshift算法的原理很简单。假设你有一堆点集，还有一个小的窗口，这个窗口可能是圆形的，现在你可能要移动这个窗口到点集密度最大的区域当中。

最开始的窗口是蓝色圆环的区域，命名为C1。蓝色圆环的圆心用一个蓝色的矩形标注，命名为C1_o。

而窗口中所有点的点集构成的质心在蓝色圆形点C1_r处，显然圆环的形心和质心并不重合。所以，移动蓝色的窗口，使得形心与之前得到的质心重合。在新移动后的圆环的区域当中再次寻找圆环当中所包围点集的质心，然后再次移动，通常情况下，形心和质心是不重合的。不断执行上面的移动过程，直到形心和质心大致重合结束。 这样，最后圆形的窗口会落到像素分布最大的地方，也就是图中的绿色圈，命名为C2。

meanshift算法除了应用在视频追踪当中，在聚类，平滑等等各种涉及到数据以及非监督学习的场合当中均有重要应用，是一个应用广泛的算法。

图像是一个矩阵信息，如何在一个视频当中使用meanshift算法来追踪一个运动的物体呢？ 大致流程如下：

• 首先在图像上选定一个目标区域
• 计算选定区域的直方图分布，一般是HSV色彩空间的直方图。
• 对下一帧图像b同样计算直方图分布。
• 计算图像b当中与选定区域直方图分布最为相似的区域，使用meanshift算法将选定区域沿着最为相似的部分进行移动，直到找到最相似的区域，便完成了在图像b中的目标追踪。
• 重复3到4的过程，就完成整个视频目标追踪。
  通常情况下我们使用直方图反向投影得到的图像和第一帧目标对象的起始位置，当目标对象的移动会反映到直方图反向投影图中，meanshift 算法就把我们的窗口移动到反向投影图像中灰度密度最大的区域了。
  

直方图反向投影的流程是：
假设我们有一张100x100的输入图像，有一张10x10的模板图像，查找的过程是这样的：

• 从输入图像的左上角(0,0)开始，切割一块(0,0)至(10,10)的临时图像；
• 生成临时图像的直方图；
• 用临时图像的直方图和模板图像的直方图对比，对比结果记为c；
• 直方图对比结果c，就是结果图像(0,0)处的像素值；
• 切割输入图像从(0,1)至(10,11)的临时图像，对比直方图，并记录到结果图像；
• 重复1～5步直到输入图像的右下角，就形成了直方图的反向投影。

cv.meanShift(probImage, window, criteria)

参数:

• probImage: ROI区域，即目标的直方图的反向投影
• window： 初始搜索窗口，就是定义ROI的rect
• criteria: 确定窗口搜索停止的准则，主要有迭代次数达到设置的最大值，窗口中心的漂移值大于某个设定的限值等。

实例:

import numpy as np
import cv2 as cv
# 1.获取图像
cap = cv.VideoCapture('DOG.wmv')

# 2.获取第一帧图像，并指定目标位置
ret,frame = cap.read()
# 2.1 目标位置（行，高，列，宽）
r,h,c,w = 197,141,0,208  
track_window = (c,r,w,h)
# 2.2 指定目标的感兴趣区域
roi = frame[r:r+h, c:c+w]

# 3. 计算直方图
# 3.1 转换色彩空间（HSV）
hsv_roi =  cv.cvtColor(roi, cv.COLOR_BGR2HSV)
# 3.2 去除低亮度的值
# mask = cv.inRange(hsv_roi, np.array((0., 60.,32.)), np.array((180.,255.,255.)))
# 3.3 计算直方图
roi_hist = cv.calcHist([hsv_roi],[0],None,[180],[0,180])
# 3.4 归一化
cv.normalize(roi_hist,roi_hist,0,255,cv.NORM_MINMAX)

# 4. 目标追踪
# 4.1 设置窗口搜索终止条件：最大迭代次数，窗口中心漂移最小值
term_crit = ( cv.TERM_CRITERIA_EPS | cv.TERM_CRITERIA_COUNT, 10, 1 )

while(True):
    # 4.2 获取每一帧图像
    ret ,frame = cap.read()
    if ret == True:
        # 4.3 计算直方图的反向投影
        hsv = cv.cvtColor(frame, cv.COLOR_BGR2HSV)
        dst = cv.calcBackProject([hsv],[0],roi_hist,[0,180],1)

        # 4.4 进行meanshift追踪
        ret, track_window = cv.meanShift(dst, track_window, term_crit)

        # 4.5 将追踪的位置绘制在视频上，并进行显示
        x,y,w,h = track_window
        img2 = cv.rectangle(frame, (x,y), (x+w,y+h), 255,2)
        cv.imshow('frame',img2)

        if cv.waitKey(60) & 0xFF == ord('q'):
            break        
    else:
        break
# 5. 资源释放        
cap.release()
cv.destroyAllWindows()

下面是三帧图像的跟踪结果：

5.2.1 Camshift
大家认真看下上面的结果，有一个问题，就是检测的窗口的大小是固定的，而狗狗由近及远是一个逐渐变小的过程，固定的窗口是不合适的。所以我们需要根据目标的大小和角度来对窗口的大小和角度进行修正。CamShift可以帮我们解决这个问题。

CamShift算法全称是“Continuously Adaptive Mean-Shift”（连续自适应MeanShift算法），是对MeanShift算法的改进算法，可随着跟踪目标的大小变化实时调整搜索窗口的大小，具有较好的跟踪效果。

Camshift算法首先应用meanshift，一旦meanshift收敛，它就会更新窗口的大小，还计算最佳拟合椭圆的方向，从而根据目标的位置和大小更新搜索窗口。如下图所示：

Camshift在OpenCV中实现时，只需将上述的meanshift函数改为Camshift函数即可：
将Camshift中的：

 # 4.4 进行meanshift追踪
        ret, track_window = cv.meanShift(dst, track_window, term_crit)

        # 4.5 将追踪的位置绘制在视频上，并进行显示
        x,y,w,h = track_window
        img2 = cv.rectangle(frame, (x,y), (x+w,y+h), 255,2)

改为:

  #进行camshift追踪
    ret, track_window = cv.CamShift(dst, track_window, term_crit)

        # 绘制追踪结果
        pts = cv.boxPoints(ret)
        pts = np.int0(pts)
        img2 = cv.polylines(frame,[pts],True, 255,2)