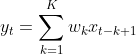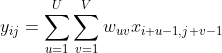【八问八答】卷积神经网络

目录

1. 为什么提出卷积神经网络

2. 卷积的含义、类型有什么

一维卷积

二维卷积

卷积的类型有什么

 3. 卷积层是什么、性质有什么

卷积层含义

卷积层性质

4. 汇聚层是什么

汇聚层含义

汇聚层类型

5. 典型的卷积网络结构是什么

6. 典型的卷积神经网络有什么

1）LeNet-5

2）AlexNet

3）Inception网络

4）残差网络

7. 图像中常用的滤波器及对应的特征映射是什么

8. 互相关是什么含义

---

1. 为什么提出卷积神经网络

卷积神经网络主要针对图像处理。在卷积神经网络之前最常用的是全连接神经网络模型。但是在用全连接前馈网络来处理 图像时，会存在以下两个问题：

（1）参数太多：如果输入图像大小为100 × 100 × 3（即图像高度为100，宽度 为100以及RGB 3个颜色通道），在全连接前馈网络中，第一个隐藏层的每个神经 元到输入层都有100 × 100 × 3 = 30 000个互相独立的连接，每个连接都对应一个 权重参数. 随着隐藏层神经元数量的增多，参数的规模也会急剧增加. 这会导致 整个神经网络的训练效率非常低，也很容易出现过拟合.

（2）局部不变性特征：自然图像中的物体都具有局部不变性特征，比如尺度 缩放、平移、旋转等操作不影响其语义信息. 而全连接前馈网络很难提取这些局部 不变性特征，一般需要进行数据增强来提高性能.

2. 卷积的含义、类型有什么

卷积（Convolution），也叫褶积，是分析数学中一种重要的运算. 在信号处 理或图像处理中，经常使用一维或二维卷积.

一维卷积

假 设滤波器长度为，它和一个信号序列1 , 2 , ⋯的卷积为

 信号序列和滤波器的卷积定义为

其中∗表示卷积运算.

一般情况下滤波器的长度 远小于信号序列长度.

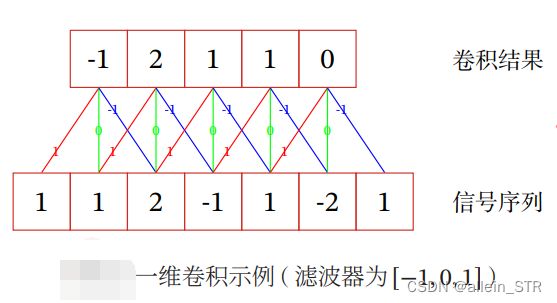
一维卷积 示例如图所示.

滤波器为[−1, 0, 1]，连接边上的数字为滤波器中的权重

 

二维卷积

卷积也经常用在图像处理中. 因为图像为一个二维结构，所以需要 将一维卷积进行扩展. 给定一个图像 和滤波器，一般 << , << ，其卷积为

一个输入信息 和滤波器 的二维卷积定义为

其中∗表示二维卷积运算

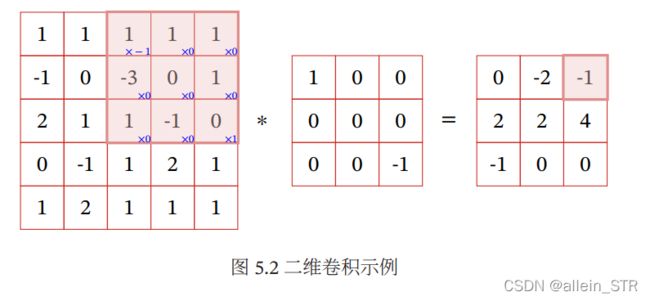
二维卷积示例如图所示

卷积的类型有什么

一般常用的卷积有以下三类：

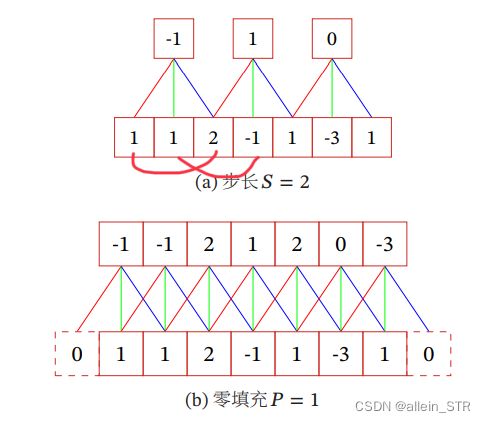
（1） 窄卷积（Narrow Convolution）：步长 = 1，两端不补零 = 0，卷积后输 出长度为 − + 1.

（2） 宽卷积（Wide Convolution）：步长 = 1，两端补零 = − 1，卷积后输 出长度 + − 1.

（3） 等宽卷积（Equal-Width Convolution）：步长 = 1，两端补零 = ( − 1)/2，卷积后输出长度. 等宽卷积示例如图所示

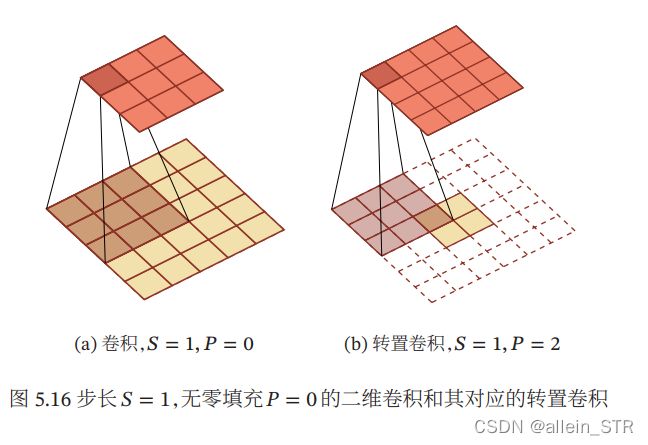
（4）转置卷积：将 低维特征映射到高维特征的卷积操作称为转置卷积（Transposed Convolution） [Dumoulin et al., 2016]，也称为反卷积（Deconvolution）[Zeiler et al., 2011]

在卷积网络中，卷积层的前向计算和反向传播也是一种转置关系.

对一个 维的向量 ，和大小为 的卷积核，如果希望通过卷积操作来映射 到更高维的向量，只需要对向量 进行两端补零 = − 1，然后进行卷积，可以 即宽卷积. 得到 + − 1维的向量.

转置卷积同样适用于二维卷积. 下图给出了一个步长 = 1，无零填充 = 0的二维卷积和其对应的转置卷积

 （5）微步卷积：我们可以通过增加卷积操作的步长 > 1 来实现对输入特征的下采 样操作，大幅降低特征维数. 同样，我们也可以通过减少转置卷积的步长 < 1 来实现上采样操作，大幅提高特征维数. 步长 < 1的转置卷积也称为微步卷积。

（Fractionally-Strided Convolution）[Long et al., 2015]. 为了实现微步卷积，我 们可以在输入特征之间插入0来间接地使得步长变小. 如果卷积操作的步长为 > 1，希望其对应的转置卷积的步长为 1 ，需要在输 入特征之间插入 − 1个0来使得其移动的速度变慢. 以一维转置卷积为例，对一个 维的向量，和大小为 的卷积核，通过对向 量进行两端补零 = − 1，并且在每两个向量元素之间插入 个0，然后进行 步长为1的卷积，可以得到( + 1) × ( − 1) + 维的向量.

下图给出了一个步长 = 2，无零填充 = 0 的二维卷积和其对应的转置 卷积.

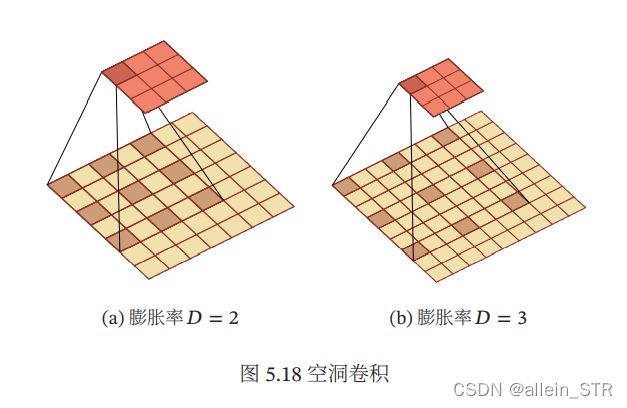
 （6）空洞卷积：空洞卷积（Atrous Convolution）是一种不增加参数数量，同时增加输出 单元感受野的一种方法，也称为膨胀卷积（Dilated Convolution）[Chen et al.,2018; Yu et al., 2015]. 空洞卷积通过给卷积核插入“空洞”来变相地增加其大小. 如果在卷积核的每两个元素之间插入 − 1个空洞，卷积核的有效大小为

其中 称为膨胀率（Dilation Rate）. 当 = 1时卷积核为普通的卷积核.

空洞卷积的示例如下图所示

 

 3. 卷积层是什么、性质有什么

卷积层含义

卷积层的作用是提取一个局部区域的特征，不同的卷积核相当于不同的特征 提取器.

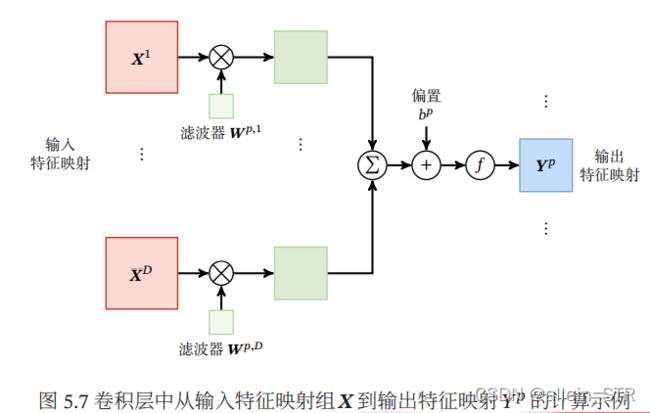
通常将神经元组织为三维结构的神经层，其大小为高度 × 宽度 ×深度，由 个 × 大小的        

特征映射构成. 特征映射（Feature Map）为一幅图像（或其他特征映射）在经过卷积提取 到的特征，每个特征映射可以作为一类抽取的图像特征. 为了提高卷积网络的表 示能力，可以在每一层使用多个不同的特征映射，以更好地表示图像的特征.

在输入层，特征映射就是图像本身. 如果是灰度图像，就是有一个特征映射， 输入层的深度 = 1；如果是彩色图像，分别有RGB三个颜色通道的特征映射，输 入层的深度 = 3

卷积层的三维结构如图所示：

 在输入为 ∈ ℝ××，输出为 ∈ ℝ′×′× 的卷积层中，每一个输出特征 映射都需要 个滤波器以及一个偏置. 假设每个滤波器的大小为 × ，那么共 需要 × × ( × ) + 个参数.

卷积层性质

根据卷积的定义，卷积层有两个很重要的性质：

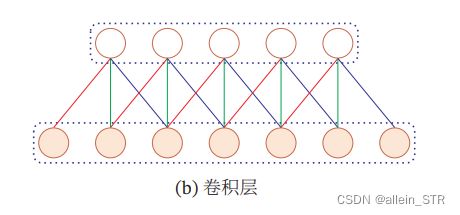
局部连接：在卷积层（假设是第 层）中的每一个神经元都只和下一层（第 − 1 层）中某个局部窗口内的神经元相连，构成一个局部连接网络. 如图所示，卷 积层和下一层之间的连接数大大减少，由原来的 × −1 个连接变为 × 个 连接， 为滤波器大小.

权重共享：作为参数的滤波器() 对于第 层的所有的神 经元都是相同的. 如图所示中，所有的同颜色连接上的权重是相同的. 权重共享可 以理解为一个滤波器只捕捉输入数据中的一种特定的局部特征. 因此，如果要提 取多种特征就需要使用多个不同的滤波器.

由于局部连接和权重共享，卷积层的参数只有一个 维的权重() 和1维的 偏置 ()，共 + 1个参数. 参数个数和神经元的数量无关. 此外，第 层的神经元 个数不是任意选择的，而是满足 = −1 − + 1.

4. 汇聚层是什么

汇聚层含义

汇聚层（Pooling Layer）也叫子采样层（Subsampling Layer），其作用是进 行特征选择，降低特征数量，从而减少参数数量

卷积层虽然可以显著减少网络中连接的数量，但特征映射组中的神经元个数 并没有显著减少. 如果后面接一个分类器，分类器的输入维数依然很高，很容易出 现过拟合. 为了解决这个问题，可以在卷积层之后加上一个汇聚层，从而降低特征 维数，避免过拟合.

汇聚层类型

常用的汇聚函数有两种：

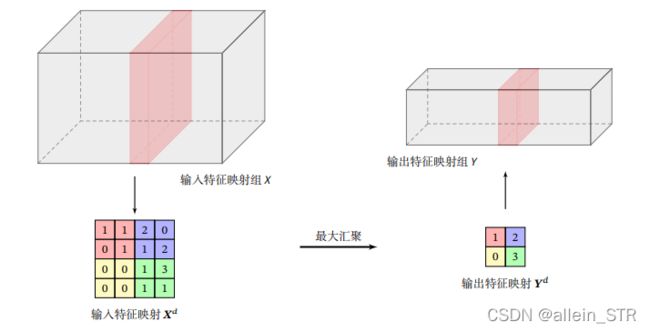
1. 最大汇聚（Maximum Pooling 或 Max Pooling），选 择这个区域内所有神经元的最大活性值作为这个区域的表示

可以看出，汇聚层不但可 以有效地减少神经元的数量，还可以使得网络对一些小的局部形态改变保持不变 性，并拥有更大的感受野. 

2. 平均汇聚（Mean Pooling）：一般是取区域内所有神经元活性值的平均 值

5. 典型的卷积网络结构是什么

一个典型的卷积网络是由卷积层、汇聚层、全连接层交叉堆叠而成. 目前 常用的卷积网络结构如图5.9所示. 一个卷积块为连续 个卷积层和 个汇聚层 （ 通常设置为2 ∼ 5，为0或1）. 一个卷积网络中可以堆叠 个连续的卷积块， 然后在后面接着 个全连接层（ 的取值区间比较大，比如1 ∼ 100或者更大； 一般为0 ∼ 2）.

目前，整个网络结构趋向于使用更小的卷积核（比如 1 × 1 和 3 × 3）以及更 深的结构（比如层数大于 50） 

6. 典型的卷积神经网络有什么

1）LeNet-5

LeNet-5的网络结构如图所示.

LeNet-5共有7层，接受输入图像大小为32 × 32 = 1 024，输出对应10个类别 的得分. LeNet-5中的每一层结构如下：

（1） C1层是卷积层，使用6个5 × 5的滤波器，得到6组大小为28 × 28 = 784的 特征映射. 因此，C1层的神经元数量为6 × 784 = 4704，可训练参数数量为 6 × 25 + 6 = 156，连接数为156 × 784 = 122304（包括偏置在内，下同）.

（2） S2层为汇聚层，采样窗口为2 × 2，使用平均汇聚，并使用如下的非线性函数.

神经元个数为 6 × 14 × 14 = 1176，可训练参数数量为 6 × (1 + 1) = 12，连接数为6 × 196 × (4 + 1) = 5880.

（3） C3 层为卷积层. LeNet-5 中用一个连接表来定义输入和输出特征映射之间的依赖关系. 如图所示：

共使用60个5 × 5的滤波器，得到16组大小为 10 × 10 的特征映射. (60 × 25) + 16 = 1 516，连接数为100 × 1 516 = 151600

（4） S4层是一个汇聚层，采样窗口为2 × 2，得到16个5 × 5大小的特征映射，可 训练参数数量为16 × 2 = 32，连接数为16 × 25 × (4 + 1) = 2000.

（5） C5 层是一个卷积层，使用 120 × 16 = 1 920 个 5 × 5 的滤波器，得到 120 组 大小为 1 × 1 的特征映射. C5 层的神经元数量为 120，可训练参数数量为 1 920 × 25 + 120 = 48 120，连接数为120 × (16 × 25 + 1) = 48120.

（6） F6层是一个全连接层，有84个神经元，可训练参数数量为84 × (120 + 1) = 10 164. 连接数和可训练参数个数相同，为10164.

（7） 输出层：输出层由10个径向基函数（Radial Basis Function，RBF）组成. 

2）AlexNet

AlexNet[Krizhevsky et al., 2012] 是第一个现代深度卷积网络模型，其首次 使用了很多现代深度卷积网络的技术方法，比如使用GPU进行并行训练，采用了 ReLU 作为非线性激活函数，使用 Dropout 防止过拟合，使用数据增强来提高模 型准确率等

AlexNet 的结构如图所示，包括 5 个卷积层、3 个汇聚层和 3 个全连接层 （其中最后一层是使用 Softmax 函数的输出层）.

AlexNet的输入为224 × 224 × 3的图像，输出为1 000个类别的条件概率，具 体结构如下：

（1） 第一个卷积层，使用两个大小为11 × 11 × 3 × 48的卷积核，步长 = 4，零 填充 = 3，得到两个大小为55 × 55 × 48的特征映射组.

（2） 第一个汇聚层，使用大小为 3 × 3 的最大汇聚操作，步长 = 2，得到两个 27 × 27 × 48的特征映射组. 

（3） 第二个卷积层，使用两个大小为5 × 5 × 48 × 128的卷积核，步长 = 1，零 填充 = 2，得到两个大小为27 × 27 × 128的特征映射组

（4） 第二个汇聚层，使用大小为3 × 3的最大汇聚操作，步长 = 2，得到两个大 小为13 × 13 × 128的特征映射组.

（5） 第三个卷积层为两个路径的融合，使用一个大小为 3 × 3 × 256 × 384的卷积 核，步长 = 1，零填充 = 1，得到两个大小为13 × 13 × 192的特征映射组.

（6） 第四个卷积层，使用两个大小为 3 × 3 × 192 × 192的卷积核，步长 = 1，零 填充 = 1，得到两个大小为13 × 13 × 192的特征映射组.

（7） 第五个卷积层，使用两个大小为3 × 3 × 192 × 128的卷积核，步长 = 1，零 填充 = 1，得到两个大小为13 × 13 × 128的特征映射组.

（8） 第三个汇聚层，使用大小为3 × 3的最大汇聚操作，步长 = 2，得到两个大 小为6 × 6 × 128的特征映射组.

（9） 三个全连接层，神经元数量分别为4 096、4 096和1 000.

3）Inception网络

在 Inception 网络中，一个卷积层包含多个不同大小的卷积操作，称为Inception 模 块. Inception网络是由有多个Inception模块和少量的汇聚层堆叠而成.

Inception模块同时使用1 × 1、3 × 3、5 × 5等不同大小的卷积核

下图给出了 v1 版本的 Inception 模块结构，采用了 4 组平行的特征抽取方 式，分别为1 × 1、3 × 3、5 × 5的卷积和3 × 3的最大汇聚. 同时，为了提高计算效 率，减少参数数量，Inception模块在进行3 × 3、5 × 5的卷积之前、3 × 3的最大汇 聚之后，进行一次1 × 1的卷积来减少特征映射的深度. 如果输入特征映射之间存 在冗余信息，1 × 1的卷积相当于先进行一次特征抽取

Inception 网络有多个版本，其中最早的 Inception v1 版本就是非常著名的 GoogLeNet [Szegedy et al., 2015]

GoogLeNet由9个 LeNet致敬. Inception v1模块和5个汇聚层以及其他一些卷积层和全 连接层构成，总共为22层网络，如下图所示

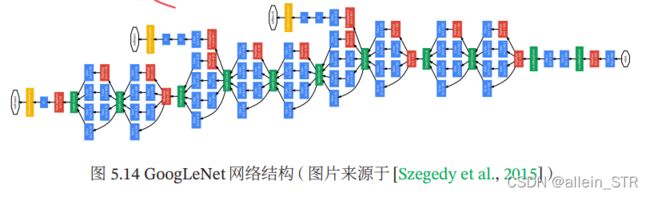. 为了解决梯度消失问题，GoogLeNet 在网络中间层引入两个辅助分类器来 加强监督信息. 

Inception 网络有多个改进版本，其中比较有代表性的有 Inception v3 网络 [Szegedy et al., 2016]. Inception v3 网络用多层的小卷积核来替换大的卷积核， 以减少计算量和参数量，并保持感受野不变. 具体包括：（1）使用两层 3 × 3 的卷 积来替换v1中的5 × 5的卷积；（2）使用连续的 × 1和1 × 来替换 × 的卷 积. 此外，Inception v3 网络同时也引入了标签平滑以及批量归一化等优化方法 进行训练.

4）残差网络

残差网络（Residual Network，ResNet）通过给非线性的卷积层增加直连边 （Shortcut Connection）的方式来提高信息的传播效率.

假设在一个深度网络中，我们期望一个非线性单元（可以为一层或多层的卷 积层）(; )去逼近一个目标函数为ℎ(). 如果将目标函数拆分成两部分：恒等 函数（Identity Function）和残差函数（Residue Function）

 根据通用近似定理，一个由神经网络构成的非线性单元有足够的能力来近似逼近 原始目标函数或残差函数，但实际中后者更容易学习 [He et al., 2016].

下图给出了一个典型的残差单元示例. 残差单元由多个级联的（等宽）卷 积层和一个跨层的直连边组成，再经过ReLU激活后得到输出.

残差网络就是将很多个残差单元串联起来构成的一个非常深的网络. 和残 差网络类似的还有Highway Network[Srivastava et al., 2015]. 

7. 图像中常用的滤波器及对应的特征映射是什么

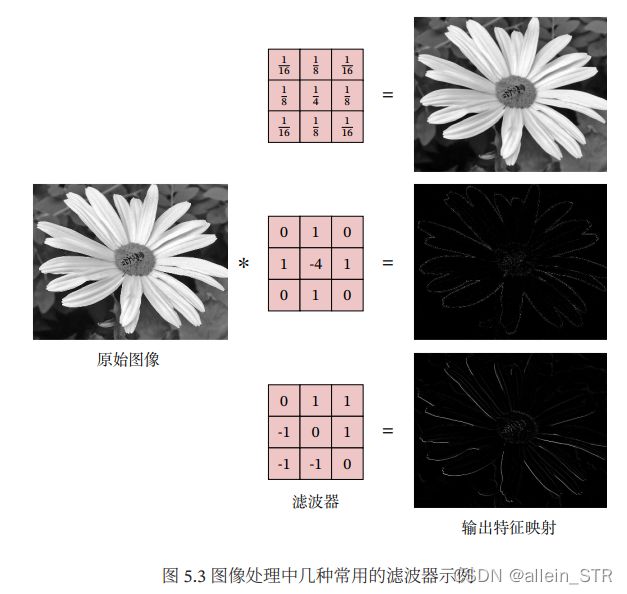
在图像处理中，卷积经常作为特征提取的有效方法. 一幅图像在经过卷积操 作后得到结果称为特征映射（Feature Map）.

图像处理中几种常用 的滤波器，以及其对应的特征映射如图所示

8. 互相关是什么含义

互相关（Cross-Correlation）是一个衡量 两个序列相关性的函数，通常是用滑动窗口的点积计算来实现. 给定一个图像和卷积核，它们的互相关为 

互相关和卷积的区别仅仅在于卷积核是否进行翻转. 因此互相关也可以称为不翻转卷积。

上述公式可以表示为：

其中⊗表示互相关运算，rot180(⋅)表示旋转180度， ∈ ℝ−+1,−+1 为输出矩阵.