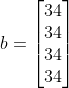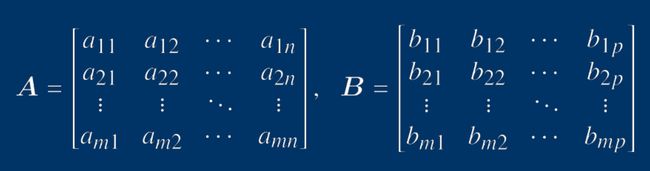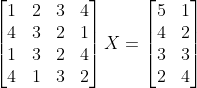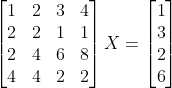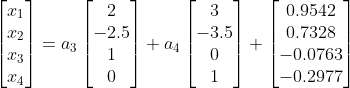基于MATLAB的求解线性方程组(附完整代码和例题)
目录
前言
一. 直接求解:矩阵除法
例题1
例题2
例题3
二. 直接求解:判断求解
2.1 m=n且rank(A)=rank(C)=n
2.2 rank(A)=rank(C)=r<>
例题5
2.3
三. 矩阵求逆解线性方程组
例题 6
前言
线性方程组的直接解法方法很多,包括Gauss消去法、选主元消去法、平方根法和追赶法等等。但是在MATLAB中,可以直接利用“\”或者“/”来解决问题。这两种方法的内部包含非常多的自适应算法,比如对超定方程使用最小二乘法;对欠定方程给出误差范数最小的一个解;对三对角阵方程组使用追赶法。
一. 直接求解:矩阵除法
对线性方程![]() 求解,MATLAB调用格式如下:
求解,MATLAB调用格式如下:
x=A\B调用此函数时,矩阵A、B必须具有相同的行数。如果矩阵A没有正确缩放或者接近奇异矩阵,运行代码时,MATLAB就会显示警告信息。
对矩阵A可以分成如下三种情况:
- 如果A是标量,那么A\B就等同于A.\B
- 如果A是
方阵,B是n行矩阵,那么A\B就是方程A*X=B的解
- 如果A是
矩阵,而且
,B是m行矩阵,那么A\B返回方程组A*X=B的最小二乘解
例题1
解如下方程:
解:
MATLAB代码如下:
clc;clear;
A=[0.4096 0.1234 0.3678 0.2943;0.2246 0.3872 0.4015 0.1129;
0.3645 0.1920 0.3781 0.0643;0.1784 0.4002 0.2786 0.3927];
b=[0.4043;0.1150;0.4240;-0.2557];
x=A\b;
x' %将结果输出为行向量 运行结果:
ans =
0.332683779325239 -1.412140862756104 1.602847655449206 -0.500293786006566
例题2
A为4阶的幻方矩阵,求解线性方程组Ax=b。b的表达式如下:
备注:幻方矩阵的定义:如果一个数组具有相同行列且每行,每列和对角线上的和都一样,则成这些数组则成为魔方矩阵,又叫幻方矩阵。
解:
MATLAB代码如下:
clc;clear;
A=magic(4); %生成四阶的幻方矩阵
b=[34;34;34;34];
x=A\b;
x'
运行结果:
ans =
0.980392156862745 0.941176470588235 1.058823529411765 1.019607843137255
分析:
4阶的幻方矩阵是奇异矩阵,奇异矩阵也能求解,但是MATLAB会生成警告,警告信息如下:
警告: 矩阵接近奇异值,或者缩放错误。结果可能不准确。RCOND = 4.625929e-18。
例题3
对线性方程组Ax=b进行求解,并分析是否有误差。A,b矩阵如下:
解:
MATLAB代码如下:
clc;clear;
A=[1 2 0;0 4 3];
b=[8;18];
x=A\b
E=norm(b-A*x) %求范数误差运行结果:
x =
0
3.999999999999997
0.666666666666670
E =
7.160723346098895e-15
分析:此方程属于欠定方程,MATLAB采用最小二乘法进行求解,所以会出现误差
另外最后举一个利用稀疏矩阵对简单线性方程组Ax=B进行求解。
MATLAB代码:
clc;clear;
A=sparse([0 2 0 1 0;4 -1 -1 0 0;0 0 0 3 -6;-2 0 0 0 2;0 0 4 2 0]);%稀疏矩阵
B=sparse([8;-1;-18;8;20]); %稀疏矩阵
x=A\B
E1=norm(B-A*x) %范数误差运行结果:
x =
(1,1) 1.000000000000000
(2,1) 2.000000000000000
(3,1) 3.000000000000000
(4,1) 4.000000000000001
(5,1) 5.000000000000001
E1 =
4.189529226675416e-15
二. 直接求解:判断求解
给定矩阵A,B如下:
形成解的判定矩阵C如下:
线性方程组有解的判断定理将分成三种情况:
2.1 m=n且rank(A)=rank(C)=n
此时,方程组有唯一的解 ![]()
例题4
求解如下方程组:
解:
MATLAB代码如下:
clc;clear;
A=[1 2 3 4;4 3 2 1;1 3 2 4;4 1 3 2];
B=[5 1;4 2;3 3;2 4];
C=[A B];
%判定前提条件
rank_A=rank(A)
rank_C=rank(C)
%求解
x1=inv(A)*B
%计算范数误差
E1=norm(A*x1-B)
%计算精确解
x2=inv(sym(A))*B
%计算范数误差
E2=norm(A*x2-B)运行结果:
rank_A =4
rank_C = 4
x1 =
-1.800000000000000 2.399999999999999
1.866666666666666 -1.266666666666667
3.866666666666667 -3.266666666666667
-2.133333333333333 2.733333333333333
E1 =7.291088482824584e-15
x2 =
[ -9/5, 12/5]
[ 28/15, -19/15]
[ 58/15, -49/15]
[ -32/15, 41/15]
E2 =0
2.2 rank(A)=rank(C)=r
此时方程组有无穷多个解。将原方程组可以转化为对应的齐次方程组的解,形式如下:
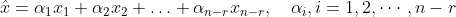
此时需要求取A矩阵的化零矩阵,MATLAB格式如下:
Z=null(A)
或者求取A矩阵的化零矩阵的规范形式,MATLAB格式如下:
Z=null(A,'r')
例题5
求解以下方程组:
解:
MATLAB代码如下:
clc;clear;
A=[1 2 3 4;2 2 1 1;2 4 6 8;4 4 2 2];
B=[1;3;2;6];
C=[A B];
%判断可解性
rank=[rank(A),rank(C)]
%求解出规范化的化零空间
Z=null(sym(A))
%求特解
x0=sym(pinv(A)*B)
%验证得出的解
a1=randn(1);
a2=rand(1); %a1和a2是不同分布的随机数
x1=a1*Z(:,1)+a2*Z(:,2)+x0;
E=norm(double(A*x1-B))
%将通解表示出来
syms a3 a4;
x2=a3*Z(:,1)+a4*Z(:,2)+x0
运行结果:
rank = 2 2
分析:说明有解,且解不止一个
Z =
[ 2, 3]
[ -5/2, -7/2]
[ 1, 0]
[ 0, 1]
分析:此结果可以解释为,如下等式:
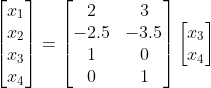
x0 =
125/131
96/131
-10/131
-39/131
E =0
分析:此方法求出的结果没有误差
x2 =
2*a3 + 3*a4 + 125/131
96/131 - (7*a4)/2 - (5*a3)/2
a3 - 10/131
a4 - 39/131
分析:此结果可以写成通式如下:
2.3 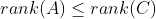
此时只能采用摩尔-彭罗斯(Moore-Penrose)广义逆求解出其最小二乘法,MATLAB格式如下:
x=pinv(A)*B
这种方法只能使误差范数测度||Ax-B||取的最小值,并不能完全符合原始的代数方程。
三. 矩阵求逆解线性方程组
通过反转系数矩阵A,也可以实现对线性方程组Ax=b的求解。不幸的是,与之前反斜杠计算的方法相比,此方法的运算速度会更慢,残差也相对较大。但其实,它也有它的优点,我们来看一道例题。
例题 6
利用八阶的幻方矩阵,来比较MATLAB中x1=A\b和x2=pinv(A)*b两种求解方法的精确度。
解:
MATLAB代码如下:
clc;clear;
A=magic(8);
A1=A(:,1:6); %行数全取,列数保留1~6列,具体原因见"分析"
rank_A1=rank(A1)
b=260*ones(8,1); %260是原A矩阵的幻数和
%使用反斜杠法求解
x1=A1\b
norm_x1=norm(x1)
E1=norm(A1*x1-b)
%使用pinv()函数求解
x2=pinv(A1)*b
norm_x2=norm(x2)
E2=norm(A1*x2-b)
运行结果:
rank_A1 =3
警告: 秩亏,秩 = 3,tol = 1.882938e-13。
(由于A1矩阵非方阵,所以运算秩时矩阵出现警告,与矩阵秩相关的介绍可以看以下文章)
基于MATLAB的矩阵性质:行列式,秩,迹,范数,特征多项式与矩阵多项式_唠嗑!的博客-CSDN博客
x1 =
2.999999999999998
4.000000000000000
0
0
1.000000000000002
0
norm_x1 = 5.099019513592784
E1 = 1.392373714442771e-13
x2 =
1.153846153846151
1.461538461538463
1.384615384615385
1.384615384615383
1.461538461538461
1.153846153846153
norm_x2 =3.281650616569467
E2 =4.019436694230464e-13
分析:
(1)将A矩阵转换为A1,因为当只有六列时,方程仍然是一致的,依旧存在解,而且解并非全由1组成。另外,由于矩阵低秩,所以会有无数个解。
(2)根据范数误差计算的结果,两种求解方法精度一致
(3)解x1的特殊之处在于它只有三个非零元素;解x2的特殊之处在于它的norm(x2)非常小
此时方程组有无穷多个解。将原方程组可以转化为对应的齐次方程组的解,形式如下:
![]()
此时需要求取A矩阵的化零矩阵,MATLAB格式如下:
Z=null(A)或者求取A矩阵的化零矩阵的规范形式,MATLAB格式如下:
Z=null(A,'r')例题5
求解以下方程组:
解:
MATLAB代码如下:
clc;clear;
A=[1 2 3 4;2 2 1 1;2 4 6 8;4 4 2 2];
B=[1;3;2;6];
C=[A B];
%判断可解性
rank=[rank(A),rank(C)]
%求解出规范化的化零空间
Z=null(sym(A))
%求特解
x0=sym(pinv(A)*B)
%验证得出的解
a1=randn(1);
a2=rand(1); %a1和a2是不同分布的随机数
x1=a1*Z(:,1)+a2*Z(:,2)+x0;
E=norm(double(A*x1-B))
%将通解表示出来
syms a3 a4;
x2=a3*Z(:,1)+a4*Z(:,2)+x0运行结果:
rank = 2 2
分析:说明有解,且解不止一个
Z =
[ 2, 3]
[ -5/2, -7/2]
[ 1, 0]
[ 0, 1]
分析:此结果可以解释为,如下等式:
x0 =
125/131
96/131
-10/131
-39/131
E =0
分析:此方法求出的结果没有误差
x2 =
2*a3 + 3*a4 + 125/131
96/131 - (7*a4)/2 - (5*a3)/2
a3 - 10/131
a4 - 39/131
分析:此结果可以写成通式如下:
2.3 
此时只能采用摩尔-彭罗斯(Moore-Penrose)广义逆求解出其最小二乘法,MATLAB格式如下:
x=pinv(A)*B这种方法只能使误差范数测度||Ax-B||取的最小值,并不能完全符合原始的代数方程。
三. 矩阵求逆解线性方程组
通过反转系数矩阵A,也可以实现对线性方程组Ax=b的求解。不幸的是,与之前反斜杠计算的方法相比,此方法的运算速度会更慢,残差也相对较大。但其实,它也有它的优点,我们来看一道例题。
例题 6
利用八阶的幻方矩阵,来比较MATLAB中x1=A\b和x2=pinv(A)*b两种求解方法的精确度。
解:
MATLAB代码如下:
clc;clear;
A=magic(8);
A1=A(:,1:6); %行数全取,列数保留1~6列,具体原因见"分析"
rank_A1=rank(A1)
b=260*ones(8,1); %260是原A矩阵的幻数和
%使用反斜杠法求解
x1=A1\b
norm_x1=norm(x1)
E1=norm(A1*x1-b)
%使用pinv()函数求解
x2=pinv(A1)*b
norm_x2=norm(x2)
E2=norm(A1*x2-b)运行结果:
rank_A1 =3
警告: 秩亏,秩 = 3,tol = 1.882938e-13。
(由于A1矩阵非方阵,所以运算秩时矩阵出现警告,与矩阵秩相关的介绍可以看以下文章)
基于MATLAB的矩阵性质:行列式,秩,迹,范数,特征多项式与矩阵多项式_唠嗑!的博客-CSDN博客
x1 =
2.999999999999998
4.000000000000000
0
0
1.000000000000002
0
norm_x1 = 5.099019513592784
E1 = 1.392373714442771e-13
x2 =
1.153846153846151
1.461538461538463
1.384615384615385
1.384615384615383
1.461538461538461
1.153846153846153
norm_x2 =3.281650616569467
E2 =4.019436694230464e-13
分析:
(1)将A矩阵转换为A1,因为当只有六列时,方程仍然是一致的,依旧存在解,而且解并非全由1组成。另外,由于矩阵低秩,所以会有无数个解。
(2)根据范数误差计算的结果,两种求解方法精度一致
(3)解x1的特殊之处在于它只有三个非零元素;解x2的特殊之处在于它的norm(x2)非常小