2.2案例：鸢尾花分类——逻辑回归

一、引言

鸢尾花数据集为机器学习常用的数据集，今天，我们基于该数据集进行算法学习

鸢尾花数据集

鸢尾花数据集有3个类别，每个类别有50个样本，其中一个类别与另外两个线性可分，另外两个线性不可分
特征：

• sepal_length花萼长度
• speal_width花萼宽度
• petal_length花瓣长度
• petal_width花瓣宽度

标签

• 0：'setosa’山鸢尾
• 1：'versicolor’变色鸢尾花
• 2:'virginica’维吉尼亚鸢尾花

二、鸢尾花分类

鸢尾花数据集——提取码：1234

# 鸢尾花数据分类-PCA主成分分析降维
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.patches as mpatches
import warnings
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import accuracy_score
np.random.seed(0)

# 加载数据
def loaddata():
    columns = ['sepal_length', 'speal_width', 'petal_length', 'petal_width', 'type']
    data = pd.read_csv('data/iris.data', header=None, names=columns)
    # 将类别信息转化为数值信息
    data['type'] = pd.Categorical(data['type']).codes
    data = data.values
    X = data[:, :-1]
    y = data[:, -1]
    return X, y


def plotPCA():
    # 将降维后的数据进行绘图
    mpl.rcParams['font.sans-serif'] = ['simHei']
    mpl.rcParams['axes.unicode_minus'] = False

    cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
    # 根据y自动选择颜色
    plt.scatter(X[:, 0], X[:, 1], c=np.array(y).squeeze(), cmap=cm_dark, marker='o')
    plt.grid(b=True, ls=':')
    plt.xlabel(u'组分1', fontsize=14)
    plt.ylabel(u'组分2', fontsize=14)
    plt.title('鸢尾花数据PCA降维', fontsize=18)
    plt.show()

def plotDescionBoundary():

    fig = plt.figure(facecolor='w')
    fig.subplots()
    cm_light = mpl.colors.ListedColormap(['#77E0A0','#FF8080','#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
    # 伪彩图
    plt.pcolormesh(X1,X2,y_pred_show,cmap=cm_light)
    # 样本的显示
    plt.scatter(X[:,0],X[:,1],s=30,c=y,edgecolors='k',cmap=cm_dark)
    # 标签
    plt.xlabel('组分1',fontsize=15)
    plt.ylabel('组分2',fontsize=15)
    # 网格
    plt.grid(b=True,ls=':')

    patchs = [mpatches.Patch(color='#77E0A0', label='Iris-setosa'),
              mpatches.Patch(color='#FF8080', label='Iris-versicolor'),
              mpatches.Patch(color='#A0A0FF', label='Iris-virginica')]
    # 设置图例
    # fancybox=True:控制是否应在构成图例背景的FancyBboxPatch周围启用圆边
    # framealpha=0.8:控制图例框架的 Alpha 透明度
    # loc:图例所有figure位置
    plt.legend(handles=patchs, fancybox=True, framealpha=0.8, loc='lower right')

    # 标题
    plt.title(u'鸢尾花Logistic回归分类效果', fontsize=17)
    plt.show()

if __name__ == '__main__':
    # 消除警告
    warnings.filterwarnings(action='ignore')
    # 设置显示宽度
    pd.set_option('display.width', 1000)
    # 加载数据
    X, y = loaddata()

    # 特征工程—— PCA降维
    # pca降维后在所有数据中所占比例，一般是80%
    pca = PCA(n_components=2, whiten=True, random_state=0)
    X = pca.fit_transform(X)
    print('各方向方差:', pca.explained_variance_)
    print('方差所占比例:', pca.explained_variance_ratio_)

    # PCA降维后进行绘图
    plotPCA()

    # 数据分割
    X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7)

    # 逻辑回归模型
    model = Pipeline([
        ('ploy', PolynomialFeatures(degree=2, include_bias=True)),
         ('lgc', LogisticRegressionCV(Cs=np.logspace(-3, 4, 8), fit_intercept=False, cv=5))
    ])
    model.fit(X_train, y_train)
    print('最佳参数为', model.get_params('lgc')['lgc'].C_)
    # 预测
    y_train_pred = model.predict(X_train)
    print('训练集的准确率为',accuracy_score(y_train_pred,y_train))
    y_test_pred = model.predict(X_test)
    print('测试集的准确率为',accuracy_score(y_test_pred,y_test))

    # 对得到的结果进行绘制
    # 横纵采样500个点
    N,M = 500,500
    X1_min,X1_max = min(X[:,0])-0.5,max(X[:,0])+0.5
    X2_min,X2_max = min(X[:,1])-0.5,max(X[:,1])+0.5
    # 生成等距数组
    t1 = np.linspace(X1_min,X1_max,N)
    t2 = np.linspace(X2_min,X2_max,M)

    # 生成网格采样点
    # meshgrid适用于生成网格型数据，接受两个一维数组，生成两个二维矩阵
    X1,X2 = np.meshgrid(t1,t2)

    # 生成测试点
    X_show = np.stack((X1.flat,X2.flat),axis=1)
    # 预测
    y_pred_show = model.predict(X_show)
    # 使之与输入的形状相同
    y_pred_show = y_pred_show.reshape(X1.shape)

    # 画决策边界图
    plotDescionBoundary()

各方向方差: [4.22484077 0.24224357]
方差所占比例: [0.92461621 0.05301557]
最佳参数为 [1. 1. 1.]
训练集的准确率为 0.9619047619047619
测试集的准确率为 0.9777777777777777

当degree=2时，

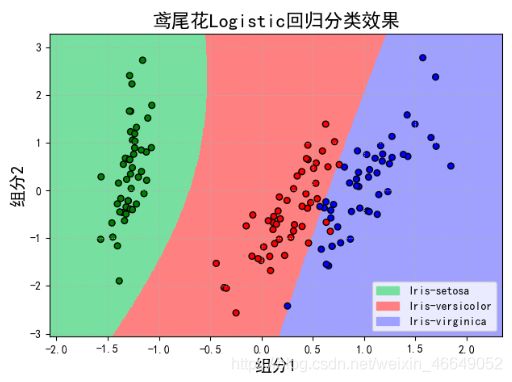
当degree=3时，

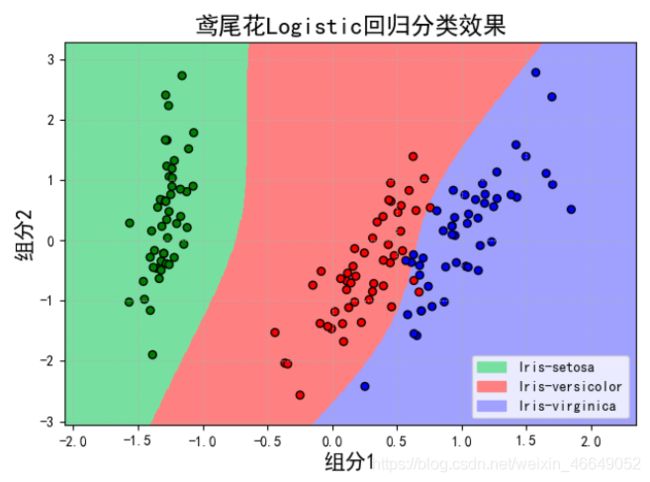
当degree=4时，

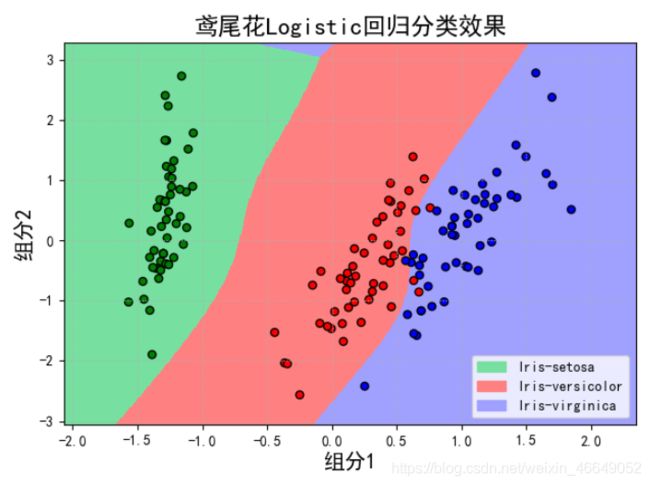
当做线性回归预测时，为了提高模型的泛化能力，经常采用多次线性函数来建立模型，次数越多，学习内容越多，但也容易造成过拟合。