离散数学习题
离散数学习题
- 图论
- 命题逻辑
- 谓词逻辑
- 集合与关系
- 函数
- 代数系统
图论
1.
C
解析:根据邻接矩阵的定义进行表示
2.下面是前缀编码的是(D )
A、010,110,01,101
B、111,000,110,11
C、10, 000, 101, 01
D、00,10,110,011
3.
A
4.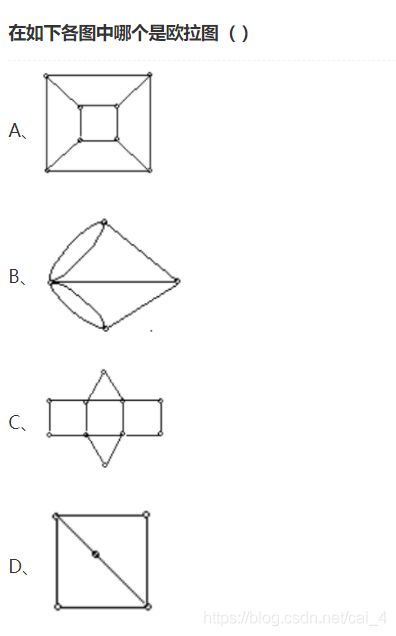
C
5.
B
6.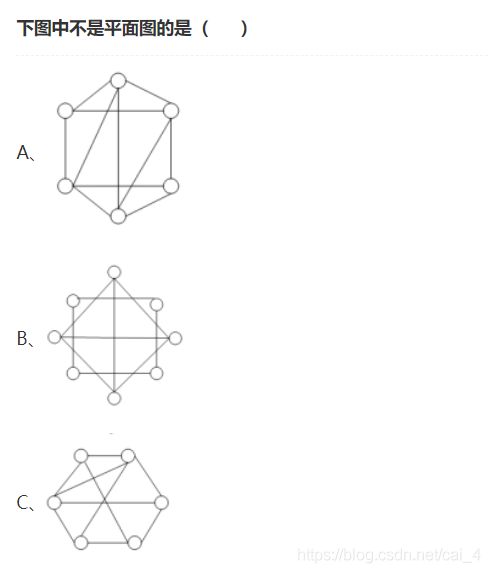
C
7.对于无孤立结点的图,下列说法正确的是?(ABCD )
A、
无向图有一条欧拉回路当且仅当图是连通的,并且所有顶点度数为偶数。
B、如果一个图中具有经过每条边一次当且仅当一次的回路,这样的图叫做欧拉图。
C、一个有向图具有单向欧拉路,当且仅当图是连通的,而且除两个顶点外,其余每个顶点的入度等于出度。而那两个顶点一个出度比入度大1,一个入度比出度大1.
D、无向图具有一条欧拉路,当且仅当图是连通的,且有两个或零个奇数度顶点。
8.以下说法正确的是(ABD )
A、任意有向图中,所有顶点的入度之和与所有顶点出度之和相等。
B、非负整数序列 (3, 3, 3, 1) 是可图化的。
C、非负整数序列 (5, 4, 3, 2, 2) 是不可图化的。
D、任意一个图中,顶点的度数之和都等于边数的两倍。
解析;非负整数序列 (5, 4, 3, 2, 2) 是可图化的。
9.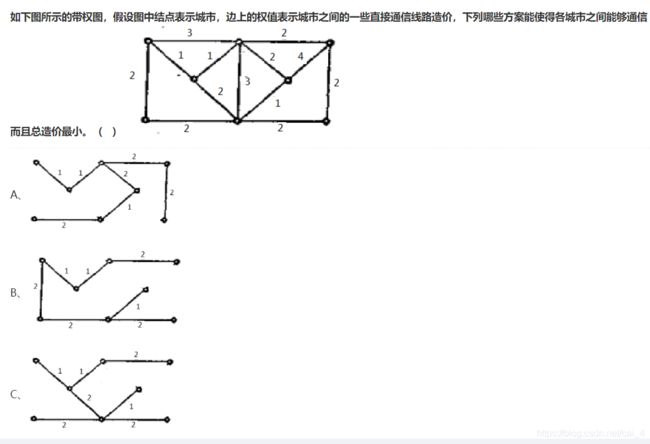
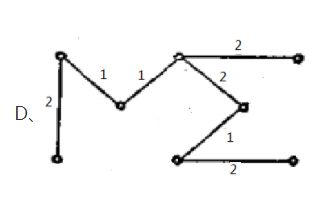
ABCD
10.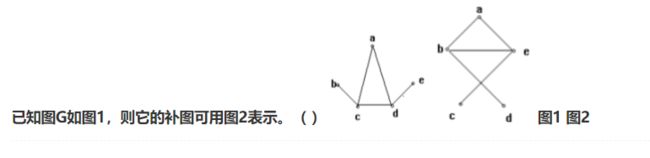
正确
命题逻辑

D
习题解析:运用命题公式翻译的步骤,选择合适的连接词将各个原子命题联结起来形成合式公式。
2.

B
3.下面句子中不是命题的是( B )
A、铅球不是球。
B、刘翔110米栏用了不到13秒,你说他是一个真正的运动健将吗?
C、刘翔110米栏用了不到13秒,他是一个真正的运动健将。
D、要是他不上场,我们就会输。
习题解析:具有确定真假值的陈述句是命题,即一个句子是命题必须同时具备两个条件:(1)首先是陈述句;(2)有确定的真值。B选项是疑问句,所以B选项不是命题。
4.以下哪个命题是原子命题?( C)
A、小明要么在上课,要么在操场跑步。
B、世界上没有救世主,也没有神仙。
C、张三和李四是朋友。
D、如果明天下雨,我就不去公园。
习题解析:原子命题是不能再分解为更为简单命题的命题;复合命题是由联结词、标点符号和原子命题复合而成的命题。
5.
B
6.
BC
7.
AC
8.下列哪些命题是复合命题( D )
A、雪是白色的。
B、两个三角形全等,当前仅当它们的三组对应边相等。
C、张三与李四是好朋友。
D、张三与李四上山。
习题解析:原子命题是不能再分解为更为简单命题的命题;复合命题是由联结词、标点符号和原子命题复合而成的命题。
9.
AD
习题解析:A选项从左边到右边的推导中利用蕴含律、交换律;D选项从左边到右边的推导中用蕴含率、交换律、结合律。
10.某医院要从A、B、C三名骨干中挑选1~2人驰援武汉疫情,由于工作需要,选派时要满足以下条件:(1)若A去,则B同去;(2)若C去,则B不能去;(3)若B不去,则A或C可以去;
请利用主范式求解下列哪些方案是可行的?( ABC )
A、B去,A,C都不去
B、C去,A、B都不去
C、A、B同去,C不去
D、以上方案都不可行
谓词逻辑
1.华苑社区已有住户向居委会报告家中发现白蚁。如果住户的报告属实,则下列陈述中能确定真假的是哪项?( C)
(1)华苑社区没有住户家中没发现白蚁。
(2)华苑社区有的住户家中没发现白蚁。
(3)华苑社区所有的住户家中都未发现白蚁。
A、仅(1)
B、仅(2)
C、仅(3)
D、(1)和(3)
E、(2)和(3)
2.
B
习题解析:B选项中∨联结词是二目运算符
3.
A
习题解析:公式中x,y是约束出现的,z是自由出现的。
4.
B
习题解析:分别用消去量词的等值式消去全称量词和存在量词
5.
C
习题解析:A选项双重否定律,B选项全称量词的分配律,D选项量词否定律,C选项不是量词辖域的收缩律。
6.
A
习题解析:A对于任意整数x都存在整数y,x + y = 0 ,B存在整数y和任意整数x相加都为0、C任意两个整数相加都为0、D不存在两个整数相加为0。
7.
BD
习题解析:所有量词在整个谓词公式的开头,其辖域可以延伸至整个公式末尾。
8.
ABC
9.
正确
习题解析:本题中用一次量词辖域的扩展即可得到该公式的前束范式。
10.
正确
习题解析:题中谓词公式的含义是:任意一个整数都是素数,显然为假。
集合与关系
1.
B
2.设A=∅,B={ ∅,{ ∅ } } ,则B-A是(D)。
A、∅
B、{ { ∅ } }
C、{ ∅ }
D、{ ∅,{ ∅ } }
3.若集合A的基数 |A|=5,则A的幂集的基数|P(A)|=( C)。
A、25
B、10
C、32
D、5
4.
C
5.
C
6.已知集合A={ 0,1},B={1,2},则集合A2×B=( BC )
A、{<0,0,1>,<0,0,2>,<0,1,1>,<0,1,2>,<1,0,1>,<1,1,1>,<1,1,2>}
B、{<0,0,1>,<0,0,2>,<0,1,1>,<0,1,2>,<1,0,1>,<1,0,2>,<1,1,1>,<1,1,2>}
C、{<<0,0>,1>,<<0,0>,2>,<<0,1>,1>,<<0,1>,2>,<<1,0>,1>,<<1,0>,2>,<<1,1>,1>,<<1,1>,2>}
D、{<0,<0,1>>,<0,<0,2>>,<0,<1,1>>,<0,<1,2>>,<1,<0,1>>,<1,<0,2>>,<1,<1,1>>,<1,<1,2>>}
7.设二元关系 R = {<1,2>,<2,4>,❤️,3>} 和 Q = {<1,3>,<2,4>,<4,2>},则 dom(R∩Q) = {2} 。(提示:不要漏掉花括号{},不要加多余的空格)
习题解析:P∩Q={<2,4>},dom(P∩Q)={2}
8.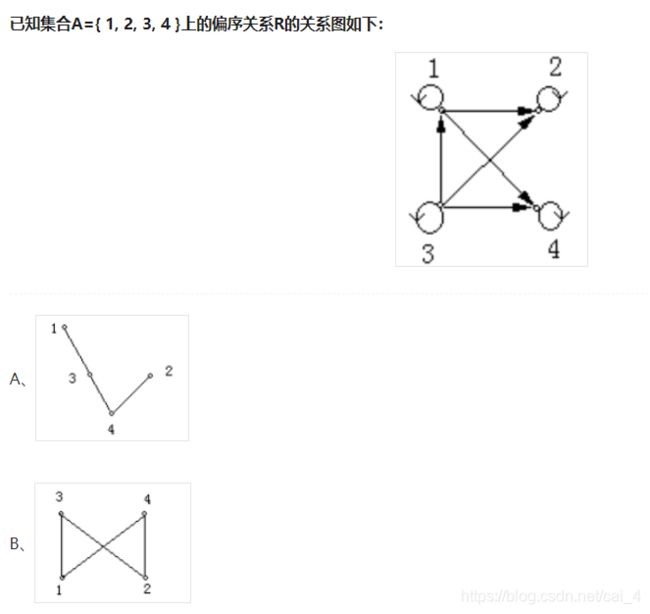
D
9.
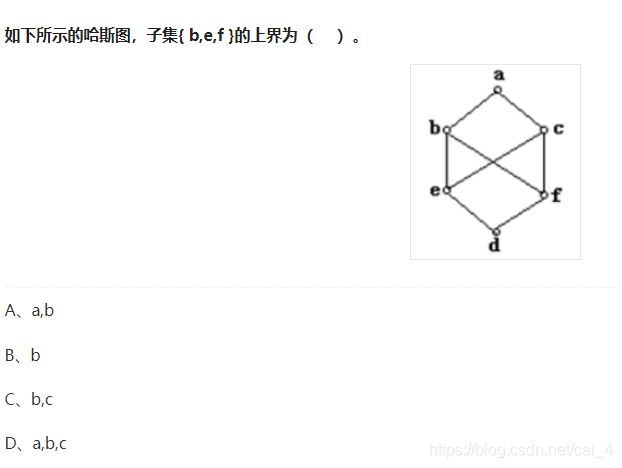
A
10.设集合X={1,2,3},下列关系中不是等价关系的是( C )。
A、A={<1,1>,<2,2>,❤️,3>}
B、B={<1,1>,<2,2>,❤️,3>,❤️,2>,<2,3>}
C、C={<1,1>,<2,2>,❤️,3>,<1,4>}
D、D={<1,1>,<2,2>,<1,2>,<2,1>,<1,3>,❤️,1>,<2,3>,❤️,2>,❤️,3>}
11.
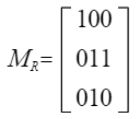
B
12.
A
13.设R1,R2,R3分别是集合{3,5,15},{1,2,3,6,12},{3,9,27,54}上的整除关系,则这三个关系中(C)是全序关系。
A、R1
B、R2
C、R3
D、无
14.设A={1,2,3,4},集合{ {1,2,3},{3,4} }和{ {1,2},{2,3},{1,3},{3,4} }都是A的覆盖,它们都能产生相同的相容关系R={<1,1>,<1,2>,<2,1>,<2,2>,<1,3>,❤️,1>,<2,3>,❤️,2>,❤️,3>,❤️,4>,<4,3>,<4,4>}
正确
15.若关系R是自反的,当且仅当在关系矩阵中,主对角线上所有元素都是1;在关系图上每个结点都有自回路。
正确.
函数
1.
B
2.
A
3.设X = { a,b,c }, Y = { 1,2,3 },f ={
A、f是从X到Y的二元关系,但不是从X到Y的函数。
B、f是从X 到Y的函数,但不是满射,也不是单射。
C、f是从X到Y的满射,但不是单射。
D、f是从 X 到 Y 的双射。
4.
D
5.
AC
6.![]()
A、x+4
B、x-4
C、(x+4)-1
D、x
B
7.
正确
8.
A
9.
A
10.设A={a,b.c},B={1.2.3},则下列关系中能构成A到B函数的是( C )
A、f1 ={
B、f2={
C、f3={
D、f4={
代数系统
1.设A={1,2,…,10 },则下面定义的运算 * 关于A不封闭的有( C )。
A、xy=max(x ,y);( max(x ,y) 表示求解x和y中的最大值 )
B、xy=gcd(x , y);( gcd (x ,y) 表示求解x和y的最大公约数 )
C、xy=lcm(x ,y); ( lcm(x ,y) 表示求解x和y的最小公倍数)
D、xy=min(x ,y);( min(x ,y) 表示求解x和y中的最小值 )
习题解析:从集合A中选取x=4,y=6,lcm(4,6)=12 ∉A,所以集合A上定义的最小公倍数运算不封闭。
2.
C
习题解析:在运算表中,若某个元素所在行所在列的元素都等于该元素本身,则该元素就是该运算的零元。
3.
ABCD
习题解析:半群:满足结合律;
独异点:含有幺元的半群;
群:每个元素均可逆的含幺半群;
阿贝尔群(交换群):满足交换律的群。
4.设
A、半群
B、独异点
C、群
D、交换群
习题解析:
半群:满足集合律;
独异点:含有幺元的半群;
群:每个元素均可逆的含幺半群;
阿贝尔群(交换群):满足交换律的群。
5.
ABCD
习题解析:
独异点:含有幺元的半群;
群:每个元素均可逆的含幺半群;
阿贝尔群(交换群):满足交换律的群;
循环群:若G中存在a使得G=< a>,则称G是循环群,a为G的生成元。
6.
1、a
2、是
3、a
4、无
5、无
7.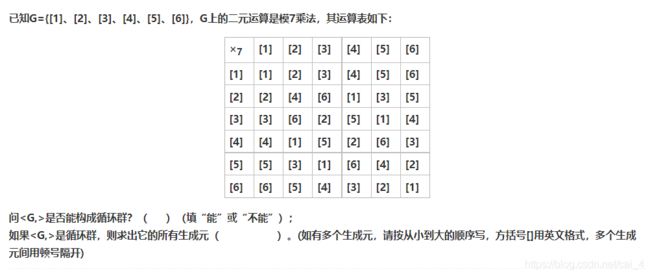
1、能
2、[3]、[5]
习题解析:
[3]×7[3]=[2]
[3]×7[3]×7[3]=[6]
[3]×7[3]×7[3]×7[3]=[4]
[3]×7[3]×7[3]×7[3]×7[3]=[5]
[3]×7[3]×7[3]×7[3]×7[3]×7[3]=[1]
[3]×7[3]×7[3]×7[3]×7[3]×7[3]×7[3]=[3]
即G中所有元素均可用[3]的幂次值表示出来,同理也可验证[5]是生成元。