我再丢dropout!
Stochastic Depth
S t o c h a s t i c Stochastic Stochastic D e p t h Depth Depth是采取类似于 D r o p o u t Dropout Dropout的思路,在 R e s N e t ResNet ResNet块上随机进行对模块的删除,进而提高对模型的泛化能力。
如图所示,为 S t o c h a s t i c Stochastic Stochastic D e p t h Depth Depth的具体做法。

用数学化的语言来表示下该过程就是:
若网络总共有 L L L 个 b l o c k block block,我们给每个 b l o c k block block都加上了一个概率 p l p_{l} pl 。
在训练时:
根据 p l p_{l} pl 用一个 b e r n o u l l i bernoulli bernoulli随机变量生成每个 b l o c k block block的激活状态 b l b_{l} bl,最终把 R e s N e t ResNet ResNet的 b o t t l e n e c k bottleneck bottleneck b l o c k block block,从 H l = ReL U ( f l ( H l − 1 ) + i d t e n t i t y ( H l − 1 ) ) H_{l}=\operatorname{ReL} U\left(f_{l}\left(H_{l-1}\right)+idtentity\left(H_{l-1}\right)\right) Hl=ReLU(fl(Hl−1)+idtentity(Hl−1))调整成了 H l = ReLU ( b l f l ( H l − 1 ) + i d t e n t i t y ( H l − 1 ) ) H_{l}=\operatorname{ReLU}\left(b_{l} f_{l}\left(H_{l-1}\right)+idtentity\left(H_{l-1}\right)\right) Hl=ReLU(blfl(Hl−1)+idtentity(Hl−1))。
其中,当 b l = 0 b_{l}=0 bl=0时,表明这个 b l o c k block block未被激活,此时 H l = ReL U ( i d e n t i t y ( H l − 1 ) ) H_{l}=\operatorname{ReL} U\left(identity\left(H_{l-1}\right)\right) Hl=ReLU(identity(Hl−1))。特别地是。其中 p l p_{l} pl是从 p 0 = 1 p_{0}=1 p0=1线性衰减到 p L = 0.5 p_{L}=0.5 pL=0.5,即 p l = 1 − l L ( 1 − p L ) p_{l}=1-\frac{l}{L}\left(1-p_{L}\right) pl=1−Ll(1−pL)。
在预测的时候:
b l o c k block block被定义为:
H l T e s t = ReL U ( p l f l ( H l − 1 Test ) + i d e n t i t y ( H l − 1 Test ) ) H_{l}^{T e s t}=\operatorname{ReL} U\left(p_{l} f_{l}\left(H_{l-1}^{\text {Test }}\right)+identity\left(H_{l-1}^{\text {Test }}\right)\right) HlTest=ReLU(plfl(Hl−1Test )+identity(Hl−1Test ))。相当于将 p l p_{l} pl与该层的残差做了一个权值融合了。
个人觉得这样 D r o p Drop Drop有以下两个好处:
- ,这种引入随机变量的设计有效的克服了过拟合使模型有了更好的泛化能力。这种 D r o p Drop Drop的方式,本质上一种模型融合的方案。由于训练时模型的深度随机,预测时模型的深度确定,事实上是在测试时把不同深度的模型融合了起来。
- 以往的 D r o p o u t Dropout Dropout或者 D r o p C o n n e c t DropConnect DropConnect都主要是在全连接层进行,这里是对整个网络进行 D r o p Drop Drop的。
这里给出一个参考代码如下:
class BottleNeck(nn.Module):
def __init__(self, in_channels, out_channels, stride):
super(BottleNeck, self).__init__()
self.conv1 = nn.Sequential(
nn.Conv2d(in_channels=in_channels, out_channels=out_channels, kernel_size=1),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=True)
)
self.conv2 = nn.Sequential(
nn.Conv2d(in_channels=out_channels, out_channels=out_channels, kernel_size=3, stride=stride, padding=1),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=True)
)
self.conv3 = nn.Sequential(
nn.Conv2d(in_channels=out_channels, out_channels=(out_channels * 4), kernel_size=1),
nn.BatchNorm2d((out_channels * 4)),
nn.ReLU(inplace=True)
)
self.relu = nn.ReLU(inplace=True)
self.downsample = nn.Sequential(
nn.Conv2d(in_channels=in_channels, out_channels=(out_channels * 4), kernel_size=1, stride=stride),
nn.BatchNorm2d((out_channels * 4))
)
def forward(self, x, active):
if self.training:
if active == 1:
print("active")
identity = x
identity = self.downsample(identity)
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = x + identity
x = self.relu(x)
return(x)
else:
print("inactive")
x = self.downsample(x)
x = self.relu(x)
return(x)
else:
identity = x
identity = self.downsample(identity)
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.prob * x + identity
x = self.relu(x)
return(x)
Cutout
目前为主,丢的主要是权重,或者是丢的是神经元。这里开始,我们要丢的是是网络的输入,当然网络输入不仅仅可以丢,也可以添加噪声( C u t m i x Cutmix Cutmix等),这个是后面要做的内容。当然,还有一些对于输入图像进行 D r o p Drop Drop的操作(如 r a n d o m random random e r a s e erase erase),我这里先打个样,看下如何对输入图像进行丢弃。后面补充下,其它丢弃输入图像的操作。
先看看 C u t o u t Cutout Cutout的做法:
图像上进行随机位置和一定大小的 p a t c h patch patch进行 0 − m a s k 0-mask 0−mask裁剪。一开始使用裁剪上采样等变换出复杂轮廓的 p a t c h patch patch,后来发现简单的固定像素 p a t c h patch patch就可以达到不错的效果,所以直接采用正方形 p a t c h patch patch。
通过 p a t c h patch patch的遮盖可以让网络学习到遮挡的特征。 C u t o u t Cutout Cutout不仅能够让模型学习到如何辨别他们,同时还能更好地结合上下文从而关注一些局部次要的特征。
C u t o u t Cutout Cutout的效果图如下所示:
参考代码如下:
import torch
import numpy as np
class Cutout(object):
"""Randomly mask out one or more patches from an image.
Args:
n_holes (int): Number of patches to cut out of each image.
length (int): The length (in pixels) of each square patch.
"""
def __init__(self, n_holes, length):
self.n_holes = n_holes
self.length = length
def __call__(self, img):
"""
Args:
img (Tensor): Tensor image of size (C, H, W).
Returns:
Tensor: Image with n_holes of dimension length x length cut out of it.
"""
h = img.size(1)
w = img.size(2)
mask = np.ones((h, w), np.float32)
for n in range(self.n_holes):
y = np.random.randint(h) # 返回随机数/数组(整数)
x = np.random.randint(w)
y1 = np.clip(y - self.length // 2, 0, h) #截取函数
y2 = np.clip(y + self.length // 2, 0, h) #用于截取数组中小于或者大于某值的部分,
x1 = np.clip(x - self.length // 2, 0, w) #并使得被截取的部分等于固定的值
x2 = np.clip(x + self.length // 2, 0, w)
mask[y1: y2, x1: x2] = 0.
mask = torch.from_numpy(mask) #数组转换成张量,且二者共享内存,对张量进行修改比如重新赋值,那么原始数组也会相应发生改变
mask = mask.expand_as(img) #把一个tensor变成和函数括号内一样形状的tensor
img = img * mask
return img
C u t o u t Cutout Cutout有两个超参,不同的任务,可以自己调调实验下效果。
DropBlock
首先直观的从图片中看下 D r o p B l o c k DropBlock DropBlock的具体做法:
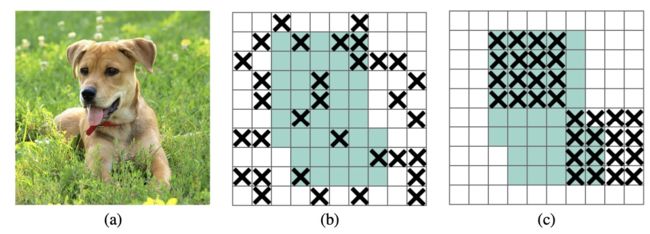
其中(b)表示的是随机 D r o p o u t Dropout Dropout的效果,©为 D r o p Drop Drop掉相邻的一整片区域,即按 S p a t i a l Spatial Spatial块随机扔。
其论文中的算法伪代码如下:
其中这个 γ \gamma γ的值,是依赖于 k e e p _ p r o b keep\_prob keep_prob的值的。其计算过程如下:
γ = 1 − k e e p _ p r o b b l o c k _ s i z e 2 f e a t _ s i z e 2 ( f e a t _ s i z e − b l o c k _ s i z e + 1 ) 2 \gamma = \frac{1-keep\_prob}{block\_size^{2}}\frac{feat\_size^{2}}{(feat\_size-block\_size+1)^{2}} γ=block_size21−keep_prob(feat_size−block_size+1)2feat_size2
k e e p _ p r o b keep\_prob keep_prob可以解释为传统的 d r o p o u t dropout dropout保留激活单元的概率, 则有效的区域为 ( f e a t _ s i z e − b l o c k _ s i z e + 1 ) 2 (feat\_size - block\_size + 1)^{2} (feat_size−block_size+1)2 , f e a t _ s i z e feat\_size feat_size 为 f e a t u r e feature feature m a p map map的 s i z e size size. 实际上 D r o p B l o c k DropBlock DropBlock中的 d r o p b l o c k dropblock dropblock可能存在重叠的区域, 因此上述的公式仅仅只是一个估计. 实验中 k e e p _ p r o b keep\_prob keep_prob设置为0.75~0.95, 并以此计算 γ \gamma γ的值。
给出一个参考的 P y t o r c h Pytorch Pytorch版本的代码:
#!/usr/bin/env python
# -*- coding:utf8 -*-
import torch
import torch.nn.functional as F
from torch import nn
class Drop(nn.Module):
def __init__(self, drop_prob=0.1, block_size=7):
super(Drop, self).__init__()
self.drop_prob = drop_prob
self.block_size = block_size
def forward(self, x):
if self.drop_prob == 0:
return x
# 设置gamma,比gamma小的设置为1,大于gamma的为0,对应第五步
# 这样计算可以得到丢弃的比率的随机点个数
gamma = self.drop_prob / (self.block_size**2)
mask = (torch.rand(x.shape[0], *x.shape[2:]) < gamma).float()
mask = mask.to(x.device)
# compute block mask
block_mask = self._compute_block_mask(mask)
# apply block mask,为算法图的第六步
out = x * block_mask[:, None, :, :]
# Normalize the features,对应第七步
out = out * block_mask.numel() / block_mask.sum()
return out
def _compute_block_mask(self, mask):
# 取最大值,这样就能够取出一个block的块大小的1作为drop,当然需要翻转大小,使得1为0,0为1
block_mask = F.max_pool2d(input=mask[:, None, :, :],
kernel_size=(self.block_size,
self.block_size),
stride=(1, 1),
padding=self.block_size // 2)
if self.block_size % 2 == 0:
# 如果block大小是2的话,会边界会多出1,要去掉才能输出与原图一样大小.
block_mask = block_mask[:, :, :-1, :-1]
block_mask = 1 - block_mask.squeeze(1)
return block_mask
结合上一篇的三种 D r o p Drop Drop策略,我们主要从主要作用在全连接网络的 D r o p o u t Dropout Dropout,作用在 C h a n n e l Channel Channel层面的 S p a t i a l Spatial Spatial D r o p o u t Dropout Dropout,作用在 L a y e r Layer Layer层面的 S t o c h a s t i c Stochastic Stochastic D r o p o u t Dropout Dropout,作用在 F e a t u r e Feature Feature m a p map map层面的 D r o p B l o c k DropBlock DropBlock,作用在输入层面的 C u t o u t Cutout Cutout等方式。给大家梳理了各个 D r o p Drop Drop方案,后面有一些列的工作是针对输入提出的正则化技巧(数据增强),在后面的文章,我们再进行补充~
这些方案具体怎么用?不好意思,需要你针对你自己的任务自己去调了。
在这里,我们要谈下,为何BN提出后,Dropout就不用了呢?
Dropout与BN不和谐共处
首先我们聊下在 P y t o r c h Pytorch Pytorch中 B N BN BN的 A P I API API:
nn.BatchNorm2d(self, num_features, eps=1e-5, momentum=0.1, affine=True, track_running_stats=True)
- num_features:输入数据的通道数,归一化时需要的均值和方差是在每个通道中计算的
- eps: 滑动平均的参数,用来计算 r u n n i n g _ m e a n running\_mean running_mean和 r u n n i n g _ v a r running\_var running_var
- affine:是否进行仿射变换,即缩放操作
- track_running_stats:是否记录训练阶段的均值和方差,即running_mean和running_var
对于 B N BN BN层的状态,包含了 5 5 5个参数:
- weight:缩放操作的 γ \gamma γ。
- bias: 缩放操作的 β \beta β
- running_mean: 训练阶段统计的均值,在测试的时候可以用到
- running_var: 训练阶段统计的方差,测试的阶段用
- num_batches_tracked,训练阶段的batch的数目,如果没有指定momentum,则用它来计算running_mean和running_var。一般momentum默认值为0.1,所以这个属性暂时没用。
假设我们的输入 t e n s o r tensor tensor的维度是 ( 4 , 3 , 2 , 2 ) (4,3,2,2) (4,3,2,2),那么我们我们在做 B N BN BN的时候,我们在 c h a n n e l channel channel维度中“抽”出来一个通道的数据,则其维度为 ( 4 , 1 , 2 , 2 ) (4,1,2,2) (4,1,2,2)。我们需要对这 16 16 16个数据求均值 μ \mu μ跟方差 σ \sigma σ,并用求得的均值与方差归一化,再缩放数据,得到 B N BN BN层的输出。
我们需要用滑动平均公式来更新 r u n n i n g _ m e a n running\_mean running_mean与 r u n n i n g _ v a r running\_var running_var, m o m e n t u m momentum momentum默认为0.1.
r u n n i n g _ m e a n = ( 1 − m o m e n t u m ) ∗ r u n n i n g _ m e a n + m o m e n t u m ∗ μ running\_mean = (1-momentum) * running\_mean + momentum * \mu running_mean=(1−momentum)∗running_mean+momentum∗μ
r u n n i n g _ v a r = ( 1 − m o m e n t u m ) ∗ r u n n i n g _ v a r + m o m e n t u m ∗ σ running\_var = (1-momentum) * running\_var + momentum * \sigma running_var=(1−momentum)∗running_var+momentum∗σ
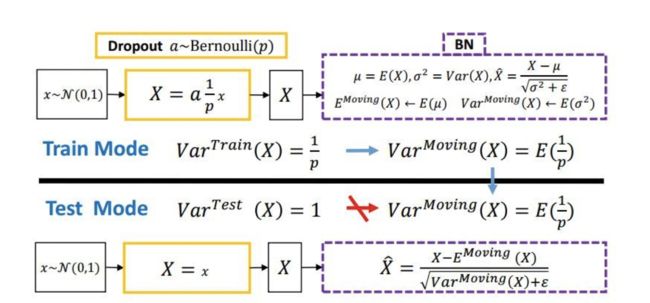
答:Dropout在网络测试的时候神经元会产生“variance shift”,即“方差偏移”。试想若有图一中的神经响应 X X X,当网络从训练转为测试时, D r o p o u t Dropout Dropout 可以通过其随机失活保留率(即 p p p)来缩放响应,并在学习中改变神经元的方差,而 B N BN BN 仍然维持 X X X 的统计滑动方差( r u n n i n g _ v a r running\_var running_var)。这种方差不匹配可能导致数值不稳定。而随着网络越来越深,最终预测的数值偏差可能会累计,从而降低系统的性能。事实上,如果没有 D r o p o u t Dropout Dropout,那么实际前馈中的神经元方差将与 B N BN BN 所累计的滑动方差非常接近,这也保证了其较高的测试准确率。
下面有张图,也比较清楚的反映了, D r o p o u t Dropout Dropout与 B N BN BN在一起使用存在的问题:
那么怎么解决这样的variance shift的问题呢?有两种方案:
- 在 B N BN BN之后,连接一个 D r o p o u t Dropout Dropout。
- 修改 D r o p o u t Dropout Dropout 的公式让它对方差并不那么敏感。有工作是进一步拓展了高斯 D r o p o u t Dropout Dropout(即不是满足伯努利分布,而是Mask满足高斯分布),提出了一个均匀分布 D r o p o u t Dropout Dropout,这样做带来了一个好处就是这个形式的 D r o p o u t Dropout Dropout(又称为 “ U o u t ” “Uout” “Uout”)对方差的偏移的敏感度降低了,总得来说就是整体方差偏地没有那么厉害了。而实验我再丢! 算法必问!结果也是第二种整体上比第一个方案好,显得更加稳定。
大家好,我是灿视。目前是位算法工程师 + 创业者 + 奶爸的时间管理者!
我曾在19,20年联合了各大厂面试官,连续推出两版《百面计算机视觉》,受到了广泛好评,帮助了数百位同学们斩获了BAT等大小厂算法Offer。现在,我们继续出发,持续更新最强算法面经。
我曾经花了4个月,跨专业从双非上岸华五软工硕士,也从不会编程到进入到百度与腾讯实习。
欢迎加我私信,点赞朋友圈,参加朋友圈抽奖活动。如果你想加入<百面计算机视觉交流群>,也可以私我。