数据挖掘十大算法

一、C4.5 算法

ID3 算法是以信息论为基础，以信息熵和信息增益度为衡量标准，从而实现对数据的归纳分类。ID3 算法计算每个属性的信息增益，并选取具有最高增益的属性作为给定的测试属性。

信息熵相关概念介绍：
熵：表示随机变量的不确定性。某个事件发生的概率越高，熵越小。熵的计算公式如下：

条件熵：在一个条件下，随机变量的不确定性。
信息增益：熵 - 条件熵。表示在一个条件下，信息不确定性减少的程度。

举个例子，X(明天下雨)是一个随机变量，X的熵可以算出来， Y(明天阴天)也是随机变量，在阴天情况下下雨的信息熵就是条件熵。X的熵减去Y条件下X的熵，就是信息增益。具体解释：原本明天下雨的信息熵是2，条件熵是0.01（因为如果知道明天是阴天，那么下雨的概率很大，信息量少），这样相减后为1.99。在获得阴天这个信息后，下雨信息不确定性减少了1.99，不确定减少了很多，所以信息增益大。也就是说，阴天这个信息对明天下午这一推断来说非常重要。

C4.5 算法核心思想是ID3 算法，是ID3 算法的改进，改进方面有：
1）用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足；
2）在树构造过程中进行剪枝；
3）能处理非离散的数据；
4）能处理不完整的数据；

C4.5 算法优点：产生的分类规则易于理解，准确率较高。
缺点：
1)在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。
2)C4.5 只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。

二、K-Means 算法

K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，让簇间的距离尽量的大。

如果用数据表达式表示，假设簇划分为(C1,C2,…Ck)，则我们的目标是最小化平方误差J：

其中N 为样本数，K 是簇数，rnk表示n 属于第k 个簇，uk 是第k 个中心点的值。然后求出最优的uk

KMeans算法图解如下：

1. 图a表示初始数据集，假设k=2。
2. 图b中，随机选择2个类所对应的质心，即图中的红色质心和蓝色质心。
3. 然后分别求样本中所有点到这两个质心的距离，并根据距离最小的质心的类别标记每个样本的类别，如图c所示，经过计算样本和红色质心和蓝色质心的距离，我们得到了所有样本点的第一轮迭代后的类别。
4. 此时对当前标记为红色和蓝色的点分别求其新的质心，如图4所示，新的红色质心和蓝色质心的位置已经发生了变动。
5. 图e和图f重复了我们在图c和图d的过程，即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。

在实际K-Mean算法中，我们一般会多次运行图c和图d，才能达到最终的比较优的类别。

优点：算法速度很快
缺点：分组的数目k 是一个输入参数，不合适的k 可能返回较差的结果。

三、朴素贝叶斯算法

朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法。算法的基础是概率问题，分类原理是通过某对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类的概率，选择具有最大后验概率的类作为该对象所属的类。

下面通过举例来理解贝叶斯公式：
贝叶斯的思想是执果索因，就是在知道结果的情况下去推断原因的方法。通过现象（结果）去推断事情发生的本质（原因）。
假设产生结果有两个原因：A、B ， 这里假设A、B = {原因}， H = {结果}

全概率公式：H发生的可能性
P(H) = P(H|A)P(A) + P(H|B)P(B)
贝叶斯公式: 在H发生的情况下，推断是A促成的可能性
P(A|H) =P(A)P(H|A) / P(H)

举个例子：村子有且仅有两个小偷，小A和小B，根据统计A偷东西的可能性是0.2，B偷东西的可能性是0.8。如果A去偷，偷成功的概率是0.8， 如果B去偷，偷成功的概率是0.3。如果村子丢了一件东西，A和B谁是嫌疑犯的可能性更大？
H={丢东西}
A = {A去偷东西}
B = {B去偷东西}
P(A) + P(B) = 1
A，B两人偷东西可能性， P(A) = 0.2， P(B) = 0.8，这个可以从当地的派出所的案底可以统计出来，根据这两人的作案事件占比可以分析出来；A , B两人得手的可能性 P(H|A)=0.8， P(H|B)=0.3， 这个是可以根据以往这两人偷东西的能力分析得到，A的脑子可能聪明，能力大，B能力不行。那么，村子里丢东西的可能性就是 P(H) = P(A)P(H|A) + P(B)P(H|B) = 0.4，那么如果是A偷得，知道了结果H， 则可表示为 P(A|H) =P(A)P(H|A) / P(H) = 0.4。同理，如果是B偷的，丢东西的情况下，是B偷东西的概率是P(B|H) = 0.6。

朴素贝叶斯假设是约束性很强的假设，假设特征条件独立，但朴素贝叶斯算法简单，快速，具有较小的出错率。

在朴素贝叶斯的应用中，主要研究了电子邮件过滤以及文本分类研究。

四、K 最近邻分类算法（KNN）

KNN分类思想比较简单，从训练样本中找出K 个与其最相近的样本，然后看这k 个样本中哪个类别的样本多，则待判定的值就属于这个类别。

缺点：
1）K 值需要预先设定，而不能自适应；
2）当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K 个邻居中大容量类的样本占多数。

该算法适用于对样本容量比较大的类域进行自动分类。

五、EM 最大期望算法

EM 算法是基于模型的聚类方法，是在概率模型中寻找参数最大似然估计的算法，其中概率模型依赖于无法观测的隐藏变量。E 步估计隐含变量，M 步估计其他参数，交替将极值推向最大。
EM 算法比K-means 算法计算复杂，收敛也较慢，不适于大规模数据集和高维数据，但比K-means 算法计算结果稳定、准确。EM 经常用在机器学习和计算机视觉的数据集聚（Data Clustering）领域。

六、PageRank 算法

PageRank是google 的页面排序算法，是基于从许多优质的网页链接过来的网页，必定还是优质网页的回归关系，来判定所有网页的重要性。也就是说，一个人有着越多牛X 朋友的人，他是牛X 的概率就越大。

优点：
完全独立于查询，只依赖于网页链接结构，可以离线计算。
缺点：
1）PageRank 算法忽略了网页搜索的时效性。
2）旧网页排序很高，存在时间长，积累了大量的in-links，拥有最新资讯的新网页排名却很低，因为它们几乎没有in-links。

七、AdaBoost

Adaboost 是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器(弱分类器)，然后把这些弱分类器集合起来，构成一个更强的最终分类器(强分类器)。其算法本身是通过改变数据分布来实现的，它根据每次训练集之中每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练，最后将每次训练得到的分类器最后融合起来，作为最后的决策分类器。

整个过程如下所示：

1. 先通过对N 个训练样本的学习得到第一个弱分类器；
2. 将分错的样本和其他的新数据一起构成一个新的N 个的训练样本，通过对这个样本的学习得到第二个弱分类器；
3. 将和都分错了的样本加上其他的新样本构成另一个新的N个的训练样本，通过对这个样本的学习得到第三个弱分类器；
4. 如此反复，最终得到经过提升的强分类器。

目前AdaBoost 算法广泛的应用于人脸检测、目标识别等领域。

八、Apriori 算法

Apriori 算法是一种挖掘关联规则的算法，用于挖掘其内含的、未知的却又实际存在的数据关系，其核心是基于两阶段频集思想的递推算法。

Apriori 算法分为两个阶段：
1）寻找频繁项集。为了设法降低产生频繁项集的计算复杂度，可以利用支持度对候选项集进行剪枝。
2）由频繁项集找关联规则

算法缺点：
1） 每次计算项集的支持度时，都对数据库中的全部记录进行了一遍扫描比较，需要很大的I/O 负载。

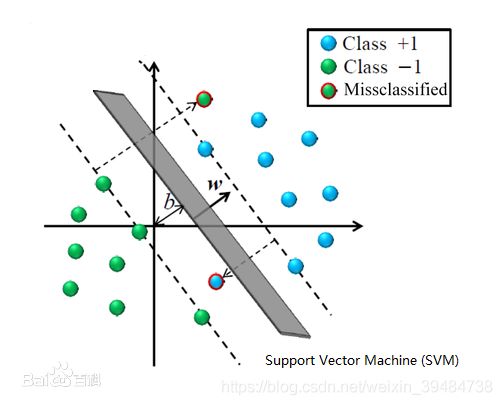
九、SVM 支持向量机

支持向量机是一种基于分类边界的方法。其基本原理是（以二维数据为例）：如果训练数据分布在二维平面上的点，它们按照其分类聚集在不同的区域。基于分类边界的分类算法的目标是，通过训练，找到这些分类之间的边界（直线的――称为线性划分，曲线的――称为非线性划分）。对于多维数据（如N 维），可以将它们视为N 维空间中的点，而分类边界就是N 维空间中的面，称为超面（超面比N维空间少一维）。线性分类器使用超平面类型的边界，非线性分类器使用超曲面。

支持向量机的原理是将低维空间的点映射到高维空间，使它们成为线性可分，再使用线性划分的原理来判断分类边界。在高维空间中是一种线性划分，而在原有的数据空间中，是一种非线性划分。

SVM 在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。

十、CART 分类与回归树

CART是一种决策树分类方法，采用基于最小距离的基尼指数估计函数，用来决定由该子数据集生成的决策树的拓展形。如果目标变量是离散的，称为分类树；如果目标变量是连续的，称为回归树。分类树是使用树结构算法将数据分成离散类的方法。

基尼指数(基尼不纯度)的计算公式如下：

算法优点：
1）非常灵活，可以允许有部分错分成本，还可指定先验概率分布，可使用自动的成本复杂性剪枝来得到归纳性更强的树。
2）在面对诸如存在缺失值、变量数多等问题时CART 显得非常稳健。