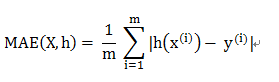2、基于Keras、Mnist手写数字识别数据集构建卷积神经网络（CNN）训练模型

---

前言

提示：本篇文章导入库函数，载入数据与本人第一篇训练模型文章一致：
1、基于Keras、Mnist手写数字识别数据集构建全连接神经网络训练模型

---

以下是本篇文章正文内容，下面案例仅供参考

一、卷积神经网络

卷积神经网络（Convolutional Neural Networks, CNN）是一类包含卷积计算且具有深度结构的前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一。卷积神经网络具有表征学习（representation learning）能力，CNN在计算机视觉，自然语言处理等领域有广泛应用。

卷积神经网络的层级结构：

• 数据输入层/ Input layer
• 卷积计算层/ CONV layer
• ReLU激励层 / ReLU layer
• 池化层 / Pooling layer
• 全连接层 / FC layer

根据个人理解，简单来说，CNN的工作原理如下:
程序接收到输入的矩阵数据后，第一步，根据设定好大小的卷积核对输入数据进行卷积运算操作，得到一个新的数据矩阵feature maps，其目的是特征提取；第二步，对这个feature maps进行池化（二次抽样），保留数据特征的同时减少数据量；第三部，重复第一步卷积层和第二步池化层的操作，第四步，经多个卷积层和池化层后，feature maps数据连接成1个或1个以上的全连接层；第五步，为了提升 CNN 网络性能，全连接层每个神经元的激励函数一般采用 ReLU 函数；最后一层全连接层的输出值被传递给一个输出，可以采用 softmax 逻辑回归（softmax regression）进行分类，最终达到识别数据识别的目的。

详细介绍可参考：https://www.cnblogs.com/skyfsm/p/6790245.html

二、构建CNN网络训练模型

1.引入库

CNN有关方法有：Dropout， Convolution2D， MaxPooling2D， Flatten

代码如下（示例）：

from keras.layers import Dense, Dropout, Convolution2D, MaxPooling2D, Flatten
from keras.models import Sequential
from keras.datasets import mnist
from keras.utils import np_utils

2.载入数据

载入数据没什么好说的，和FC

代码如下（示例）：

(x_train,y_train),(x_test,y_test) = mnist.load_data("D:\mydatasets\mnist.npz")

3.数据处理

样本数据处理

• 以训练集为例，将样本数据的维度转换为四维，(60000,28,28)->(60000,28,28,1)，其中60000代表样本的个数，（28,28）代表像素的长宽，1代表的是深度。深度为1时，表示黑白，为3时代表彩色，可以近似理解为图片的颜色通道。然后是归一化处理。

标签转换独热编码

• 对标签数据转换为分类的 one-hot （独热）编码。

代码如下（示例）：

#数据处理 (60000,28,28)->(60000,28,28,1)
x_train = x_train.reshape(-1,28,28,1)/255.0
x_test = x_test.reshape(-1,28,28,1)/255.0
y_train = np_utils.to_categorical(y_train,num_classes=10)
y_test = np_utils.to_categorical(y_test,num_classes=10)

4.创建模型

创建模型

第一层：第一层卷积层
第二层：第一层池化层
第三层：第二层卷积层
第四层：第二层池化层
第五层：扁平化
第六层：第一层全连接层
第七层：Dropout处理
第八层：第二层全连接层，输出

代码如下（示例）：

model = Sequential()
model.add(Convolution2D(                        #第一层卷积(28*28)
    input_shape = (28,28,1),
    filters = 32,
    kernel_size = 5,
    strides = 1,
    padding = 'same',
    activation = 'relu'
    ))
model.add(MaxPooling2D(                         #第一层池化(14*14),相当于28除以2
    pool_size = 2,
    strides = 2,
    padding = 'same'
    ))
model.add(Convolution2D(                        #第二层卷积
    filters = 64,
    kernel_size = 5,
    strides = 1,
    padding = 'same',
    activation = 'relu'
    ))
model.add(MaxPooling2D(                         #第二层池化
    pool_size = 2,
    strides = 2,
    padding = 'same'))
model.add(Flatten())                            #把第二个池化层的输出扁平化为一维数据
model.add(Dense(1024,activation = 'relu'))      #第一层全连接层
model.add(Dropout(0.5))                         #Dropout
model.add(Dense(10,activation = 'softmax'))     #第二层全连接层

input_shape——输入平面
filters——卷积核/滤波器个数
kernel_size——卷积窗口大小（5*5）
strides——步长
activation——激活函数
pool_size——池化的核大小
padding——填充取值：same/valid，same：在输入周围尽可能均匀填充零；valid：不适用零填充。

最简公式

         valid: [(n-f)/s + 1]  x [(n-f)/s + 1];    该公式向下取整

         same: [(n + 2p -f)/s +1] x [(n + 2p -f)/s +1];  该公式向下取整

5.编译模型

设置优化器，和目标函数，编译模型

• 本实例使用 Adam优化器；目标函数是均方误差函数。

  均方误差函数公式：

代码如下（示例）：

model.compile(optimizer='adam',loss='mse',metrics=['accuracy'])

optimizer：优化器，为预定义优化器名或优化器对象
loss：目标函数，为预定义损失函数名或一个目标函数，
metrics：设置一个评估模型的指标，该值为一个列表，包含评估模型在训练和测试时的性能的指标，典型用法是metrics=[‘accuracy’]，accuracy即精度。

6.训练模型

model.fit() 函数模型训练

代码如下（示例）：

model.fit(x_train,y_train,batch_size=32,epochs=5,verbose=2)

---

三、总代码

from keras.layers import Dense, Dropout, Convolution2D, MaxPooling2D, Flatten
from keras.models import Sequential
from keras.datasets import mnist
from keras.utils import np_utils

#载入数据
(x_train,y_train),(x_test,y_test) = mnist.load_data('D:\mydatasets\mnist.npz')
# print('x_train:',x_train.shape,'y_train:',y_train.shape)

#数据处理 (60000,28,28)->(60000,28,28,1)
x_train = x_train.reshape(-1,28,28,1)/255.0
x_test = x_test.reshape(-1,28,28,1)/255.0
y_train = np_utils.to_categorical(y_train,num_classes=10)
y_test = np_utils.to_categorical(y_test,num_classes=10)

#创建模型，输入784个神经元，输出10个神经元
model = Sequential()
model.add(Convolution2D(                        #第一层卷积(28*28)
    input_shape = (28,28,1),
    filters = 32,
    kernel_size = 5,
    strides = 1,
    padding = 'same',
    activation = 'relu'
    ))
model.add(MaxPooling2D(                         #第一层池化(14*14),相当于28除以2
    pool_size = 2,
    strides = 2,
    padding = 'same'
    ))
model.add(Convolution2D(                        #第二层卷积
    filters = 64,
    kernel_size = 5,
    strides = 1,
    padding = 'same',
    activation = 'relu'
    ))
model.add(MaxPooling2D(                         #第二层池化
    pool_size = 2,
    strides = 2,
    padding = 'same'))
model.add(Flatten())                            #把第二个池化层的输出扁平化为一维数据
model.add(Dense(1024,activation = 'relu'))      #第一层全连接层
model.add(Dropout(0.5))                         #Dropout
model.add(Dense(10,activation = 'softmax'))     #第二层全连接层

#定义优化器，编译模型
model.compile(optimizer='adam',loss='mse',metrics=['accuracy'])

#训练模型
model.fit(x_train,y_train,batch_size=32,epochs=5,verbose=2)

#评估模型
loss_train,accuracy_train = model.evaluate(x_train,y_train)
print('train loss:',loss_train,'train accuracy:',accuracy_train)
loss_test,accuracy_test = model.evaluate(x_test,y_test)
print('test loss:',loss_test,'test accuracy:',accuracy_test)

运行结果：

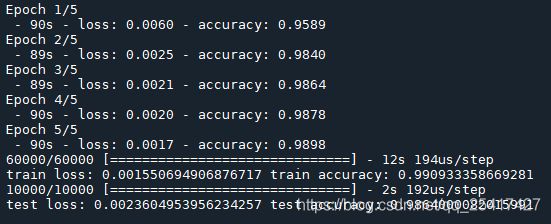
由上图可知，train accuracy的训练精度为99.0%，test accuracy的测试精度为98.6% 。