李飞飞计算机视觉笔记（3）--反向传播与神经网络初步

当前梯度值：上一层传入当前层的梯度值
两层神经网络：除开输入层总共为2层的神经网络
单层隐藏层的神经网络：与两层神经网络结构一致，我们描述神经网络的层数是通过有多少层的权值来定的，所以输入层不计入层数里面。

梯度计算

前一篇文章说了梯度计算有两种方法，一种数值方法，直接简单但速度慢，第二种就是解析方法，通过微积分进行计算，计算速度快，但有时候的结果是错误的，所以一般会进行梯度检查的操作。我们一般使用的是解析梯度方法，利用数值梯度方法对结果进行检查。
如下图所示是函数的求偏导过程，其中引入了一个中间变量$q$，损失函数对每一个权值$W_i$的偏导就用来进行优化这个权值，这个偏导实质就是梯度。在计算梯度过程中，我们不断引入中间变量，使得梯度的最终表达式是由输入值、已知值的其他变量和一些常量组成。

我们会从后向前进行求梯度，从数学的角度，梯度值越大说明这个权值对最后的损失值结果的影响就很大，即这个权值稍微变动（加一个增量）必然引起较大的损失值变动。
在求解一个权值$W_i$的梯度时，一般采用的方法是链式法则，如下图所示（这个图的例子与上图一致），这是高数中很基础的知识

利用链式法则，如下图所示，我们可以简单理解反向传播算法过程，我们先计算出q的梯度，为了得到y，我们再求出q对y的偏导，最后这两个梯度相乘就得到f对y的梯度。

反向传播算法的示意图如下图所示

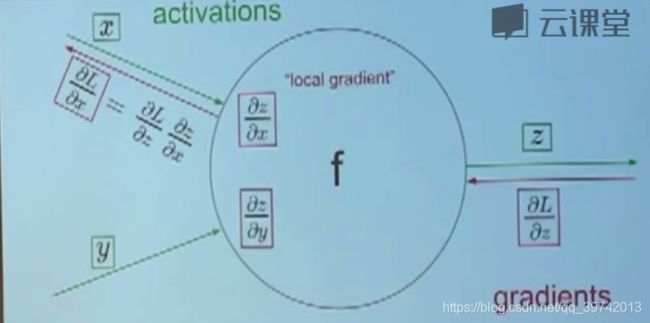
这个f可以看成是神经网络中的节点（节点实质就是一个计算），$x$、$y$为权值，$z$为输出，其中$L$为损失函数，绿色箭头线表示前向传播，红色线表示后向传播，左上角的就是$x$对$L$的影响，这里就使用了链式法则，从后向前，我们可以求得损失函数对于任何一个权值的梯度。除此之外，上图中的$x$和$y$也可以看成是上一个神经元的输出，而不看成是参数，道理和前面说的局部变量$q$类似，可以将神经元的输出就看成是由参数构成的局部变量，对此整体求偏导再对其中包含的参数求偏导，道理类似，都是使用链式法则。通过上面的讲述，如果得到的梯度是负值，那么很明显此权值增大损失值减小，如果是正值，那么权值减小损失值减小。还可以总结出，反向传播算法就是从后向前，不断乘局部梯度得到权值的梯度，依赖的法则就是链式法则。在后向传播计算梯度的过程中会用到前向传播的结果，这个只要写出前向传播的表达式很容易看出来反向传播算法就是不断利用链式法则从后向前逐层计算每一层权值的梯度。通常情况下，反向传播算法比前向传播会更慢一些，反向传播需要更多的数值参与，比如当前的梯度，它还需要对每个权值的局部梯度进行计算（这里就涉及到取上一层的输出）。

如上图所示，这里给出了一个例子反向传播sigmoid函数，助教将表达式化为了如上图的计算图，可以先写出表达式对所有输入的梯度链式，然后参照计算图从后到前计算梯度链式中的相应值。本质上就是前面提到的当前梯度乘上局部梯度，然后把求得的梯度作为当前梯度，这样不断向前，直到计算到输入层。这里和神经网络有区别，神经网络是对权值求梯度，这里是对输入求梯度，但是内在计算过程是一致的。这里的计算图是看得太细了，每个运算相互独立考虑进去。

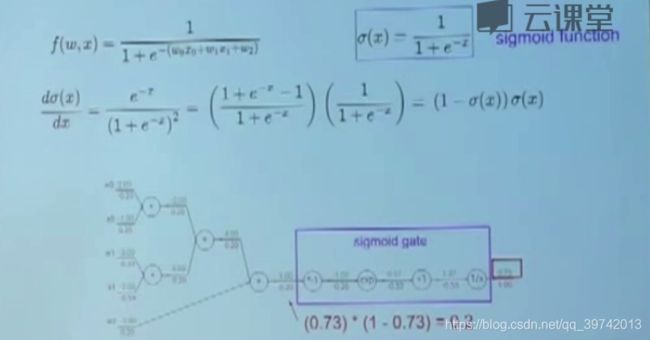
如上图助教将其中$e$的指数看成了整体，单独算局部梯度，上图中对$x$的求导过程是直接求导和链式法则结果一样，图中将表达式进行了拆分，将一些好求的式子从表达式中分解出来，单独计算局部梯度，这些局部梯度如果能够重用，那么计算速度将快于前面的不拆分方法。不能够重用也能快于前面的不拆分方法。
对于反向传播算法的过程的掌握可以帮助我们理解什么是梯度弥散（消失）。

上图中的各种gate（门），以后会发现他也被称为层，门分为如下几种

加法门(被称为 gradient distributor)

根据$L=f(z)$，$z=y+x$（$x,y$可能是两个表达式），$L$对$x$求偏导和对$y$求偏导时，他们的梯度是一样的,都为$dL/dz$，这就是加法的梯度分配，每一个加法项都会被分配相等的当前梯度值，这很好。

最大值门（gradient router）

我们考虑二元最大值门max（x，y），最大值门是将输入中的最大值最为最大值门的输出，其他输入就对输出没有贡献，所以最后的局部梯度是最大输入为1，其他为0（因为没有对输出进行贡献）。这就像路由器一样，对“路径”进行选择。最后直接将当前梯度值复制给最大输入的梯度值，而另一个输入的梯度值就为0。

乘法门

梯度交换器？我的理解是乘法门会将当前梯度值乘上另一个输入值的大小得到输入值的梯度，有“交换”输入值的意味在里面。乘法门的实现如下图（$dx=y\ast dz$）


如上图所示，当一个值通过分支被多个节点使用时，这个梯度怎么算呢？把各部分梯度加上就行。（PS 我觉得写出损失函数表达式，这些问题不是问题，按链式法则求偏导即可。按照上图中的理解和直接用损失函数求偏导结果肯定一样（这里就不举例子了，写一个例子出来就很明显了），使用上图中的方法计算梯度便于实现，对于上图这里我的理解是最后的损失值可能与上面的路径是正相关即梯度为正，下面那条路径是负相关，相加只是为了综合这两条路径，使得最终改变输入值能够使得损失值减小）。所有的神经网络都没有“回路”。
对于已经知道神经网络的人来说，神经网络因为反向传播需要一些前向传播的中间值，如有些神经元的输出值，所以在前向传播过程中会记下一下值。其实从刚才乘法门的实现中可以看出，反向传播需要输入值$x$和$y$，所以在前向传播时需要记下输入值。
在实现每一层时，一般每一层就是一个类，类中提供初始化、前馈和反馈API，供外部调用。
这里说一下雅克比矩阵，这个矩阵是一元低维导数向多元高维导数拓展的，这个矩阵的意义与一元函数中导数的意义是一样的，导数是将函数进行线性映射，即化曲为直以直近似曲，如下面公式所描述的

当$x$与$p$点相离很近时，上面的表达式就是成立的，这就是线性映射，详细的描述见WIKI百科。

向量形式的梯度求解

上面说到的都是基于一个表达式，输入值也是一个数，现在我们讨论输入值为一个向量的情况。如下图所示

形式上与单数值的一致，但是上图中的x、y和z都变为了向量，局部梯度$dz/dx$和$dz/dy$是两个雅克比矩阵，里面的数值是每一个x、y中的元素对z中的每一个元素的影响，拿$dz/dx$为例来说，假设z的元素个数有3个，x的元素个数有2个，矩阵形式如下
$$\left[\begin{array}{cc}\frac{d{z}_1}{d{x}_1}& \frac{d{z}_1}{d{x}_2}\\ & \\ \frac{d{z}_2}{d{x}_1}& \frac{d{z}_2}{d{x}_2}\\ & \\ \frac{d{z}_3}{d{x}_1}& \frac{d{z}_3}{d{x}_2}\end{array}\right]$$
我们拿$z_1$来说明，$z_1$是由$x$和$y$计算得到的，所以$z_1$的值是受这两个输入所影响的，因为我们想要计算$x$中的每一个元素对于$L$的梯度，可以不考虑$y$。$\frac{dL}{dz}$是一个向量,如下
$$\frac{dL}{dz}=\left(\frac{dL}{d{z}_1},\frac{dL}{d{z}_2},\frac{dL}{d{z}_3}\right)$$
这样我们根据链式法则可以用如下的式子计算$\frac{dL}{dx}$
$$\frac{dL}{dx}=\frac{dL}{dz}\ast \frac{dz}{dx}=\left(\frac{d{z}_1}{d{x}_1}\ast \frac{dL}{d{z}_1}+\frac{d{z}_2}{d{x}_1}\ast \frac{dL}{d{z}_2}+\frac{d{z}_3}{d{x}_1}\ast \frac{dL}{d{z}_3},\frac{d{z}_1}{d{x}_2}\ast \frac{dL}{d{z}_1}+\frac{d{z}_2}{d{x}_2}\ast \frac{dL}{d{z}_2}+\frac{d{z}_3}{d{x}_2}\ast \frac{dL}{d{z}_3}\right)$$
上面的式子就是求解向量$x$各元素对于$L$的影响，以上就是在向量情况下的后向传播，向量$y$的梯度计算和$x$类似，不再给出。其实反向传播就是反向传播梯度。
这里助教给了一个特别的例子，着重说明不是所有的雅克比矩阵都需要完整求出来，也不是所有都需要将雅克比矩阵与梯度向量相乘，因为有一些雅克比矩阵具有特殊结构，例如稀疏矩阵，例子如下所示，这里的函数是对小于0的数过滤，每一个输出只与对应的输入有关，所以这里的雅克比矩阵是一个类单位矩阵，只不过对角线上的部分1换为了0。在这种情况下，就不需要计算矩阵乘法，只需要关注哪一些输入元素值小于0，将这些元素值的梯度设为0即可，其他大于等于0的元素值的梯度设为传入进来的梯度就可以了。这样就很好的利用了此雅克比矩阵的稀疏特性，提高了效率。

在神经网络中不会出现上面的情况，因为神经网络中最终输出的是一个损失值，是一个数，所以不存在多重输出的情况（在中间的层中，如是全连接层，那么一个权值可能就会影响多个输出，从这里考虑，这个权值得到的当前梯度是一个向量），神经网络中梯度都是对权值或偏移（或者说是参数）来说的，权值之间有一定独立性（考虑全连接网络），可以把上面提到的输入理解为神经网络中的参数，是类似的。每一层都是独自处理前向和后向，也是有能力处理的。

神经网络初步

如下图所示

由前一篇文章提到的线性分类器（不含隐藏层的神经网络）可知，对于物体的不同情况，例如不同颜色，要想很好学习这些特征是很难的，拿汽车举例，汽车有黑白红蓝，假设各占1/4，因为只有一层，所以也就只有一组权值（这组权值属于汽车分类器）与输入相乘得到分数，这个权值肯定希望在某些像素点有某一些颜色，如果在这些像素点有这些颜色，那么得到的就是正值，对汽车这个类别的评分进行贡献，但是汽车摆放的位置、姿态、颜色都不一样，要对汽车进行分类，效果是比较差的，一组权值难以适应所有汽车。所以按照上图所示我们加了一层隐藏层，这个隐藏层就可以帮我们判断不同姿态、颜色的汽车，最后一层则进行综合，隐藏层对应的是各种汽车的“模板”，当测试图片与其相近的时候，得到的隐藏层中的值就是一个正值。这些节点的值是算出来的，关键在于参数的值，是W1和W2不断拟合数据。参数越多一般会更加拟合数据，效果更好，但是可能存在过拟合现象。
这里助教给出了一个例子训练两层神经网络，如下图所示

第6和第7行使用的是sigmoid激活函数，后面会介绍更多的激活函数。在第8行中对numpy中的数组执行“星运算”时执行的是矩阵的对应相乘。dot函数执行的是矩阵乘法。第8和第9行都使用了sigmoid的求导公式，即l1*（1-l1）。第8行后一部分利用sigmoid求导公式计算l2对于exp函数内整体的梯度，为什么前面有一个(y-l2)呢？又为什么最后不应该是沿负梯度减去梯度反而加上梯度呢？因为我们应该是从损失函数开始求梯度，而y-l2代表了从损失函数开始。这里为什么是y-l2我不太懂（助教说第8行这里的损失函数是逻辑回归的损失函数，大家有兴趣自行google吧），积分得到的公式$y{l}_2-1/2l_2^2$也不像是损失函数，从损失函数对l2中个元素求导考虑是有点匪夷所思，但是可以直接把y-l2向量看做是损失函数对l2的负梯度向量，因为这个向量里面负梯度的正负号是正确的，当某个元素的负梯度为负数时，即l2中此元素的数值比y中更大，加上这个负梯度能够使得l2中的数值减小，损失值减小，这符合我们对梯度的直观的认识。后面参数直接加上梯度，根据矩阵运算的性质，也正是因为将最前面的负号不断往后传递。因为梯度是有大小的，而且会进行综合，所以个人认为上面的y-l2是不合理的。关于上面有些地方求转置，可以自己画一下上面的矩阵，一目了然，可以这样理解，后向传播经历：
$前向过程中有f:R^n->R^m$从n维(x1,x2,…xn)到m维(y1,y2,…ym)的映射，为了方便理解，可以把参数看成是函数中的自变量x。后向传播时需要对函数$f$求导，得到的导数矩阵就是雅克比矩阵，矩阵中的元素就是参数x1、x2、…xn在输出值y1、y2…yn中的系数（这些系数就是前一层的输出）。那么在前向传播时某一个参数x1就会影响某一些输出如y1,y2,y3，根据上面求得的参数的导数和链式求导法则，求这些y时x1的系数和最后得到的输出值的梯度就是计算参数的梯度的数据，y1、y2和y3中x1的梯度相加就得到最终x1对于损失函数的梯度。（将x和y拓展到矩阵也是一样的道理，关键在于前一层的输出和下一层传过来的梯度，画一个图就很容易理解了）。
上图出现了一个数与矩阵或向量的运算，在numpy中，numpy会基于这些数构造一个相同shape的矩阵或向量，可以自行google：numpy中的广播机制。
其实使用后向传播比直接使用公式求梯度更快更简单。
如下图所示，就是一个神经元和一个生理上的神经元

这里的一个神经元相当于上一篇文章提到的一个类别线性分类器，很多个神经元组成就是一个完整的线性分类器，图片下面的代码就是一个神经元的前向传播实现。

激活函数

有如下几种

其中最早使用的是tanh，2012年时ReLU开始流行，因为他可以使你的神经网络变快（不知道是训练速度变快还是什么，留个坑，等助教后面讲）。你也可以定义你自己的激活函数来描述你的神经网络以及优化你的神经网络。

全连接神经网络

如下图是一个全连接神经网络，即当前层的神经元与下一层的所有神经元链接

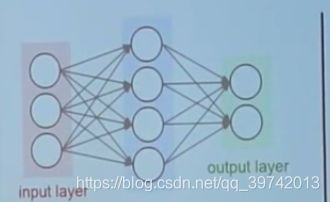
为什么要进行分层呢？因为相比将这些神经元杂乱分布，每个神经元独立进行计算，还不如将这些神经元放入各个层中，这样我们就可以进行向量化的操作，比如我们可以通过一个矩阵乘法就完成一个隐藏层中所有神经元的计算，而且同一层中的神经元的计算可以并行进行，相互不影响，他们有同样的输入。总的来说，分层化是一个计算技巧。

神经网络实例

以两层神经网络为例，我们求解二分类问题，结果如下图所示

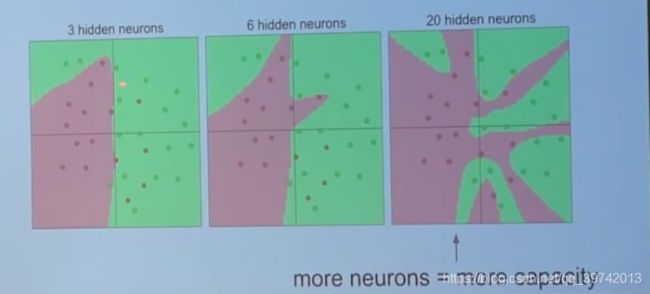
上图中3、6、20分别指隐藏层中的神经元个数，从图中可见神经元越多（参数越多）那么划分边界就越扭曲，能够解决的问题就越复杂，它能够很好拟合训练数据，但是可能存在过拟合现象，比如第三个图中，绿点里面的红点可能就是噪音，而模型却拟合了这个噪音，这不是我们期望的。
下图是使用正则化对模型分类的影响

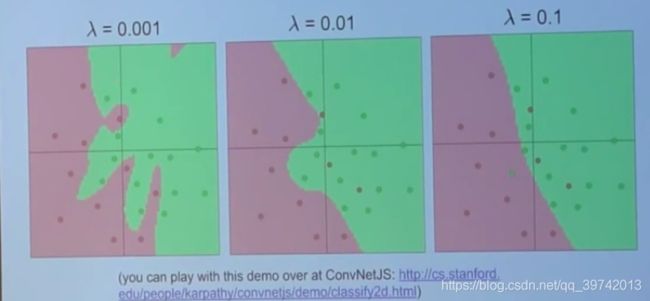
$\lambda$表示正则化系数，从图中可见$\lambda$越大，它会使w越小，w的个数越少（w很多变为了0），分类边界越平滑，但是这个系数的选择是需要实验的，不同的数据分布，$\lambda$的值可能不一样，在这里当然0.1是最好的。当减小$\lambda$时可以看见分类边界更加的扭曲，它能够解决的问题也就越复杂，w基本不为0。
如下图所示，神经网络的两种展示方法（动态图，这里是静态的）

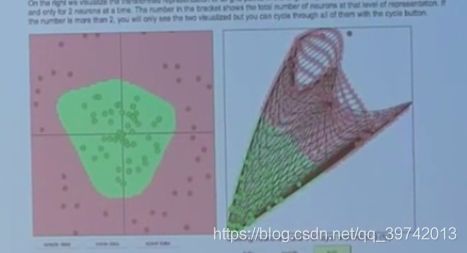
左边的就不多说了，关键是右边的。我们将网格中的点表示为红、绿类别，通过整个网格的运动来体现神经网络的动态，所以神经网络做的就是使用隐藏层将输入转换为可以使用线性分类器分类的形式，然后再用后面的层作为线性分类器进行数据分类，所以我们可以看到神经网络（隐藏层）在改变数据空间，使得后面的像线性分类器一样的层可以在这个空间中插入一个平面，通过这个平面来分类两个类别，这个概念到现在为止也是很多人工作的核心，神经网络会改变我们的数据表现形式，使得数据空间变成一个可以通过线性分类器分割的空间。
如下图所示，我们讨论在隐藏层中至少需要多少个神经元能够完成分类

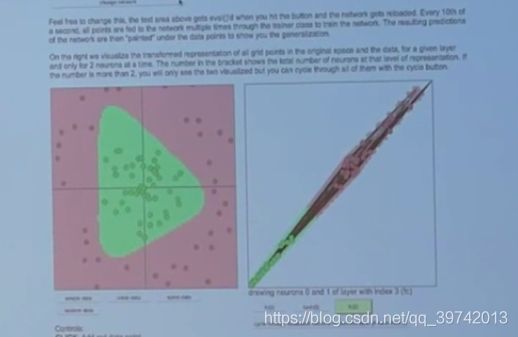
答案是3个，这三个神经元就相当于三条线，对上图中左图进行分类，每一条线都是一个类别分类器（这个线是高维空间中的，维度为输入值的维度，简单起见可以把上图中的例子看做是二维）和上一篇文章说的一样，三条线的交集就得到绿点，因是二分类问题，可以认为激活函数大于0或者大于0.5就为绿点，这个根据激活函数取值范围而定。最后一层是对这三条线进行综合输出最后结果。上面的图片是边缘带点弧线的，这个跟激活函数有关，毕竟最后神经元的输出是通过激活函数的。如果使用ReLU激活函数，那么边缘将比较尖锐（因为激活函数是一元一次函数，真的就是直线了），如下图所示


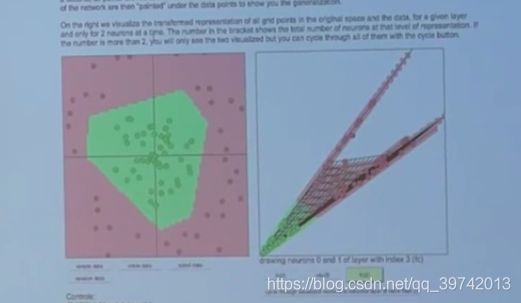
上图中实际是三条直线，为什么拐角处有边助教解释我没听懂，这里留个坑。其实上上面那个正方形也是3神经元训练出来的，到底为什么助教什么也没说就直接再训练一遍得到上图。这两个问题留个坑，等自己后面“牛逼”了再回过头看看。
对于是两个神经元的情况，很明显两条线是没办法形成闭合图形的，最后的效果如下图，是一个“通道”

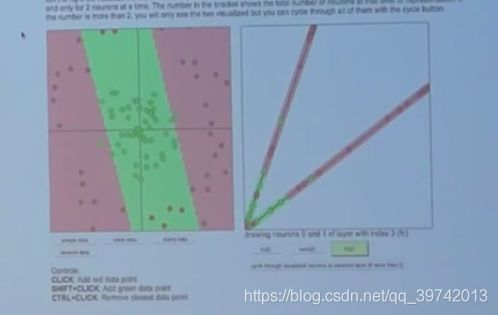
伴随着神经元的减少，意味着参数的减少，对于复杂问题来说，如果神经元过少，那么效果会很差，在越过神经元数量最小界限后，会随着神经元的减少，模型的效果越来越差，从上图中就可以看出。

总结

神经网络中的神经元越多，模型效果越好，因为在实际问题中经常出现神经网络模型的表达能力不足， 在加入大量神经元之后，需要使用正确的防止过拟合的方法，不是减少神经元，而是使用正则化处理，并对正则化参数进行合理设置。所以在实际中人们往往喜欢设置一个很大的神经网络，然后对正则化进行合理设置，其实正则化可以通过设置参数为0来减少参数的数量，但是如果考虑到训练时间，则可能选取一个小的网络进行训练。这里助教提到了另一个优化网络的算法L-BFGS，这个算法只适合小网络小数据量，一般都不会使用它，可以当做课外阅读吧拓展知识面。当然如果使用mini-batch优化网络，这个算法是个不错的选择。一般我们这整个神经网络中使用一种激活函数，不同层使用不同激活函数这个并没有什么好处，所以一般就只使用一种，但是理论上也并不一定就是错误的。