自动驾驶-基于Frenet坐标的路径规划
目录
1.什么是Frenet坐标系
2.Frenet坐标与笛卡尔坐标转化
3.五次多项式系数推导
4.基于Frenet的横向路径规划
5.基于Frenet的纵向路径规划
6.典型的路径选择方法
7.参考文献
1.什么是Frenet坐标系
我们知道在笛卡尔坐标系下，表示一个点，用（x,y），但是在自动驾驶过程中，还是希望以驾驶员视角，同时为了计算简化，我们希望车道线为参考线，相对自车，来构建一个坐标系，这就是Frenet坐标系。
如上图所示，车辆的位置在笛卡尔坐标系下坐标为（x,y）,那么在Fenet表示该位置为（s,d）。
这里的d表示车辆位置到参考线的法相距离，s表示起点到参考点的距离（注意这里是曲线长度）。
2.Frenet坐标与笛卡尔坐标转化
首先明确转换目标为：
如图所示，在某个位置，车的位置为(s,d)
其中向量 
= (cosθr,sinθr) 
= (-sinθr,cosθr) 
= (-sinθx,cosθx) 
= (cosθx,sinθx)
可以进一步推导为
（公式1）
其中的
就是参考点在笛卡尔坐标系下的坐标，因此根据d(s(t))很容易得到当前车辆坐标。
通过该式对时间t求导
其中
对d进一步求导得：
推得：
可得：
（公式2）
由该式对事件t求导
（公式3）
（公式4） 一般直接对速度事件求导，即可得到加速度
（公式5）一般直接通过三帧转为全局坐标，然后三点确定一个圆，即可得到曲率半径
3.五次多项式系数推导
为了保证舒适度，一般采用五次多项式来保证横纵向的加速度连续，因此有：
（其中的f(t) 既可以表示s(t)或d(t)）
该多项式有6个未知参数，因此要想确定一个五次多项式，必须知道起点的(位置-速度-加速度) 以及结束点的(位置-速度-加速度)
起点位置：
起点速度：
起点加速度：
结束点位置：
结束点速度：
结束点加速度：
转化为矩阵可得：
设定：
可得： 
因此求M的逆，即可求得多项式的系数。
4.基于Frenet的横向路径规划
从第三章可知，关于横向路径规划生成轨迹，最核心的是规划起始点以及结束点的位置-速度-加速度。
一般起始点为上一时刻的结束点，因此主要是选择结束点的位置-速度-加速度。
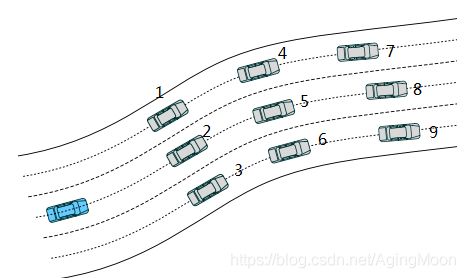
如图所示，结束点有9个备选位置，假设道路宽度为3.6m，右边移动为正，左边移动为负，则九个横向位置为(-3.6m 0 3.6m -3.6m 0 3.6m -3.6m 0 3.6m)
当然可以进一步定义末状态的预期速度和加速度。
为了获取更多的备选轨迹，我们一般会针对末状态的位置或时间，进行均匀采样（如时间选择 T+0.1,T+0.2 ...等，位置可以选择更细颗粒度），从而我们可以得到一束横向运动轨迹。
5.基于Frenet的纵向路径规划
同横向路径规划，纵向路径规划主要也是选择末状态，来确定轨迹。那么根据场景不同，对末状态的选择也有一些不同，如下表所示：
| 场景 | 末状态位置选择 | 末状态速度选择 | 末状态加速度选择 |
| 跟车场景 | 跟车位置-安全距离 | 跟车车速 | 跟车加速度 |
| 定速巡航 | 设定速度 | 限定的加速度 | 限定的加加速度 |
| 停车场景 | 目标停车位置 | 0 | 0 |
| 加塞场景 | 前后车中间安全位置 | 合理的跟车速度 | 合理的跟车加速度 |
根据不同的场景设定不同的目标点，最终通过均匀撒点，可以得到一系列纵向轨迹
虽然横纵向可以单独进行路径规划，但是在某一时刻，横纵向必须是统一的，因此针对轨迹进行一定合成，选出某一时刻既满足横向又满足纵向的轨迹。
因此需要根据时间，选出同时满足横纵向的轨迹。
6.典型的路径选择方法
根据第五和第六章，横纵向，都会基于Frenet坐标生成很多条备选轨迹，最终作为车辆参考执行的轨迹应只有一条。
那么如何选择一条最符合期望的轨迹呢？一般从以下几个维度去选择。
1.安全性，即横向与纵向 都不会与道路中的静态和动态障碍物碰撞，也包括不能行驶到车道外；
2.舒适性，一般影响舒适性的参数为横纵向的加速度，因此通过限制加速度或加加速度，可以达到舒适性目的；
3.效率，如轨迹运行时间，车速，横向位移，纵向位移等均可以作为参考因素；
4.可行性，规划出的轨迹满足车辆运动学和动力学的约束。
一般做法为，根据每项指标，设计权重（一般权重是可调参数），通过一个损耗函数 fcost = W1 * F1 + W2*F2....
其中W1为对应的权重，F1为相应的影响参数。 一般为了进一步细化，在不同的场景可以选择fcost函数。
7.参考文献
《智能车轨迹规划与算法研究》
《自动驾驶-决策与控制》