机器学习入门----线性回归实验记录

机器学习入门：线性回归实验记录

1、实验描述

• 提供一份关于产品广告费用与对应产品销量的数据文件Advertising.csv文件，利用此文件建立线性模型、训练模型、用模型做预测分析。(文件数据详见附录数据集)
• 主要步骤：
  • 加载csv文件
  • 获得标签和特征数据
  • 展示标签和特征的关系图
  • 切分数据集
  • 创建模型
  • 用模型做预测
  • 模型评估

2、相关技能

• Python编程
• Pandas编程
• Sklearn的使用
• 线性回归建模
• 用matplotlib 绘图

3、相关知识

• Pandas 读取csv文件
• Pandas读取特征、标签数据
• 数据集进行划分
• 线性模型
• 模型预测
• 模型评估

4、实现效果

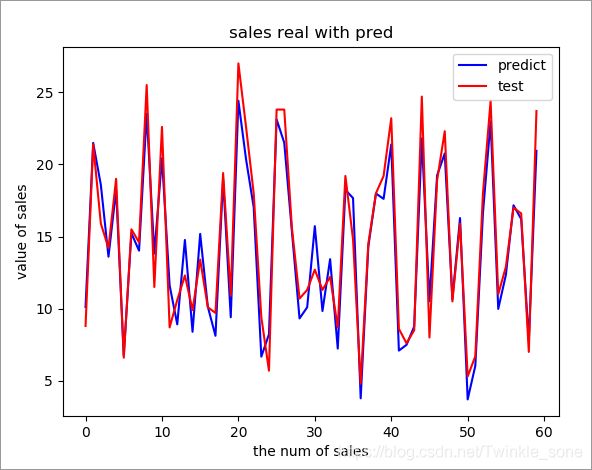
• 利用线性回归模型对测试集数据做预测，下图展示了实际销售量和预测销量的拟合效果：

5、实验步骤

5.1导入实验所需的包

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error # 均方误差

5.2读取数据文件

path = "file/Advertising.csv"
data = pd.read_csv(path)   # 读取csv文件

5.3打印文件的前几行

print(data.head(10))

5.4显示文件的shape

print(data.shape)

5.5使用pandas读取相应的维度分别作为特征值X， 和标签值Y

x = data[['TV', 'Radio', 'Newspaper']]
y = data['Sales']

5.6绘制不同特征和标签的关系

plt.figure(figsize=(9, 12))  #图示的大小
plt.subplot(311)         # 子图位于全图3行1列中的的第一个位置
plt.plot(data['TV'], y, 'ro')  # 子图的横纵坐标的两个维度；ro：其中r表示线条的颜色；o表示红色和组成（圆圈）；具体可参考下图
plt.title('TV')             # 子图的title
plt.grid()                    # 生成网格
plt.subplot(312)            # 类似
plt.plot(data['Radio'], y, 'b*')
plt.title('Radio')
plt.grid()
plt.subplot(313)
plt.plot(data['Newspaper'], y, 'g^')    # g^：表示绿色的，三角形
plt.title('Newspaper')
plt.grid()
plt.show()

下图中列出了不同字符所代表的线或者marker的样式

5.7分析上边结果图，在报纸“Newspaper”上所花广告费用与商品的销量不成线性相关的，所以后面建模时，可以尝试删掉该特征。

x=data[['TV','Radio']]

5.8使用sklearn自带的数据预处理模块对数据集进行切分，构建训练集和测试集，比例为7比3

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=23)

5.9使用sklearn的线性回归类建模，参考normalize=True表示指定对训练数据进行正则化操作；n_jobs=-1表示使用所有的cpu进行训练。

lr = LinearRegression(normalize=True, n_jobs=-1)
model = lr.fit(x_train, y_train)    # 利用训练数据，训练模型

5.10打印模型的相关参数

print(lr.intercept_)  # 打印线性模型的截距值    
print(lr.coef_)       # 返回模型的估计系数

5.11使用训练好的模型进行预测

y_pred = model.predict(x_test)

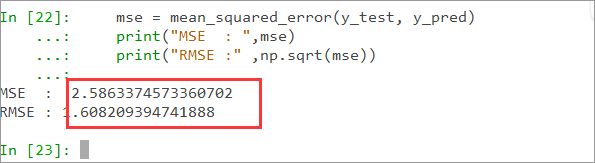
5.12使用RMSE（标准误差）对模型进行评估

mse = mean_squared_error(y_test, y_pred) # 传入实际的标签值y_test，和预测的标签值y_pred
print("MSE  : ",mse)    # MSE 均方误差    
print("RMSE :" ,np.sqrt(mse))    # 标准误差

6.4将标签的实际值和预测值用图展示出来，直观的观察拟合程度。

plt.figure()    
plt.plot(range(len(y_pred)), y_pred, 'b', label='predict')    
plt.plot(range(len(y_test)), y_test, 'r', label='test')    
plt.legend(loc='upper right') #标签的显示位置 右上角。    
plt.xlabel("the num of sales")  # x轴标签    
plt.ylabel("value of sales")     # y轴标签    
plt.title("sales real with pred")   # 图像的title    
plt.show()

7、参考答案

• 代码清单lr1.py

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error  # 均方误差
import sys

path = "file/Advertising.csv"
data = pd.read_csv(path)
print(data.head(10))
print(data.shape)
x = data[['TV', 'Radio', 'Newspaper']]
y = data['Sales']
# plt.figure(figsize=(9, 12))  #图示的大小
# plt.subplot(311)         # 子图位于全图3行1列中的的第一个位置
# plt.plot(data['TV'], y, 'ro')  # 子图的横纵坐标的两个维度；ro：其中r表示线条的颜色；o表示红色和组成（圆圈）；具体可参考下图
# plt.title('TV')             # 子图的title
# plt.grid()                    # 生成网格
# plt.subplot(312)            # 类似
# plt.plot(data['Radio'], y, 'b*')
# plt.title('Radio')
# plt.grid()
# plt.subplot(313)
# plt.plot(data['Newspaper'], y, 'g^')    # g^：表示绿色的，三角形
# plt.title('Newspaper')
# plt.grid()
# plt.show()


x=data[['TV','Radio']]
#使用sklearn自带的数据预处理模块对数据集进行切分，构建训练集和测试集，比例为7比3
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=23)
#使用sklearn的线性回归类建模，参考normalize=True表示指定对训练数据进行正则化操作；n_jobs=-1表示使用所有的cpu进行训练。
lr = LinearRegression(normalize=True, n_jobs=-1)
model = lr.fit(x_train, y_train)    # 利用训练数据，训练模型
print(lr.intercept_)  # 打印线性模型的截距值
print(lr.coef_)
y_pred = model.predict(x_test)
mse = mean_squared_error(y_test, y_pred) # 传入实际的标签值y_test，和预测的标签值y_pred
print("MSE  : ",mse)    # MSE 均方误差
print("RMSE :" ,np.sqrt(mse))    # 标准误差
plt.figure()
plt.plot(range(len(y_pred)), y_pred, 'b', label='predict')
plt.plot(range(len(y_test)), y_test, 'r', label='test')
plt.legend(loc='upper right') #标签的显示位置 右上角。
plt.xlabel("the num of sales")  # x轴标签
plt.ylabel("value of sales")     # y轴标签
plt.title("sales real with pred")   # 图像的title
plt.show()
# print(data)

8、总结

完成本次实验，可以掌握线性回归模型的基础知识，包括理论与动手编程两方面，其中编程部分涉及模型的构建、训练，以及使用matplotlib对结果进行可视化，观察不同的特征对标签的实际影响。在建模过程中，可以先删减与target呈非线性相关的特征，再建立模型、训练模型。

附录：

数据集

,TV,Radio,Newspaper,Sales
1,230.1,37.8,69.2,22.1
2,44.5,39.3,45.1,10.4
3,17.2,45.9,69.3,9.3
4,151.5,41.3,58.5,18.5
5,180.8,10.8,58.4,12.9
6,8.7,48.9,75,7.2
7,57.5,32.8,23.5,11.8
8,120.2,19.6,11.6,13.2
9,8.6,2.1,1,4.8
10,199.8,2.6,21.2,10.6
11,66.1,5.8,24.2,8.6
12,214.7,24,4,17.4
13,23.8,35.1,65.9,9.2
14,97.5,7.6,7.2,9.7
15,204.1,32.9,46,19
16,195.4,47.7,52.9,22.4
17,67.8,36.6,114,12.5
18,281.4,39.6,55.8,24.4
19,69.2,20.5,18.3,11.3
20,147.3,23.9,19.1,14.6
21,218.4,27.7,53.4,18
22,237.4,5.1,23.5,12.5
23,13.2,15.9,49.6,5.6
24,228.3,16.9,26.2,15.5
25,62.3,12.6,18.3,9.7
26,262.9,3.5,19.5,12
27,142.9,29.3,12.6,15
28,240.1,16.7,22.9,15.9
29,248.8,27.1,22.9,18.9
30,70.6,16,40.8,10.5
31,292.9,28.3,43.2,21.4
32,112.9,17.4,38.6,11.9
33,97.2,1.5,30,9.6
34,265.6,20,0.3,17.4
35,95.7,1.4,7.4,9.5
36,290.7,4.1,8.5,12.8
37,266.9,43.8,5,25.4
38,74.7,49.4,45.7,14.7
39,43.1,26.7,35.1,10.1
40,228,37.7,32,21.5
41,202.5,22.3,31.6,16.6
42,177,33.4,38.7,17.1
43,293.6,27.7,1.8,20.7
44,206.9,8.4,26.4,12.9
45,25.1,25.7,43.3,8.5
46,175.1,22.5,31.5,14.9
47,89.7,9.9,35.7,10.6
48,239.9,41.5,18.5,23.2
49,227.2,15.8,49.9,14.8
50,66.9,11.7,36.8,9.7
51,199.8,3.1,34.6,11.4
52,100.4,9.6,3.6,10.7
53,216.4,41.7,39.6,22.6
54,182.6,46.2,58.7,21.2
55,262.7,28.8,15.9,20.2
56,198.9,49.4,60,23.7
57,7.3,28.1,41.4,5.5
58,136.2,19.2,16.6,13.2
59,210.8,49.6,37.7,23.8
60,210.7,29.5,9.3,18.4
61,53.5,2,21.4,8.1
62,261.3,42.7,54.7,24.2
63,239.3,15.5,27.3,15.7
64,102.7,29.6,8.4,14
65,131.1,42.8,28.9,18
66,69,9.3,0.9,9.3
67,31.5,24.6,2.2,9.5
68,139.3,14.5,10.2,13.4
69,237.4,27.5,11,18.9
70,216.8,43.9,27.2,22.3
71,199.1,30.6,38.7,18.3
72,109.8,14.3,31.7,12.4
73,26.8,33,19.3,8.8
74,129.4,5.7,31.3,11
75,213.4,24.6,13.1,17
76,16.9,43.7,89.4,8.7
77,27.5,1.6,20.7,6.9
78,120.5,28.5,14.2,14.2
79,5.4,29.9,9.4,5.3
80,116,7.7,23.1,11
81,76.4,26.7,22.3,11.8
82,239.8,4.1,36.9,12.3
83,75.3,20.3,32.5,11.3
84,68.4,44.5,35.6,13.6
85,213.5,43,33.8,21.7
86,193.2,18.4,65.7,15.2
87,76.3,27.5,16,12
88,110.7,40.6,63.2,16
89,88.3,25.5,73.4,12.9
90,109.8,47.8,51.4,16.7
91,134.3,4.9,9.3,11.2
92,28.6,1.5,33,7.3
93,217.7,33.5,59,19.4
94,250.9,36.5,72.3,22.2
95,107.4,14,10.9,11.5
96,163.3,31.6,52.9,16.9
97,197.6,3.5,5.9,11.7
98,184.9,21,22,15.5
99,289.7,42.3,51.2,25.4
100,135.2,41.7,45.9,17.2
101,222.4,4.3,49.8,11.7
102,296.4,36.3,100.9,23.8
103,280.2,10.1,21.4,14.8
104,187.9,17.2,17.9,14.7
105,238.2,34.3,5.3,20.7
106,137.9,46.4,59,19.2
107,25,11,29.7,7.2
108,90.4,0.3,23.2,8.7
109,13.1,0.4,25.6,5.3
110,255.4,26.9,5.5,19.8
111,225.8,8.2,56.5,13.4
112,241.7,38,23.2,21.8
113,175.7,15.4,2.4,14.1
114,209.6,20.6,10.7,15.9
115,78.2,46.8,34.5,14.6
116,75.1,35,52.7,12.6
117,139.2,14.3,25.6,12.2
118,76.4,0.8,14.8,9.4
119,125.7,36.9,79.2,15.9
120,19.4,16,22.3,6.6
121,141.3,26.8,46.2,15.5
122,18.8,21.7,50.4,7
123,224,2.4,15.6,11.6
124,123.1,34.6,12.4,15.2
125,229.5,32.3,74.2,19.7
126,87.2,11.8,25.9,10.6
127,7.8,38.9,50.6,6.6
128,80.2,0,9.2,8.8
129,220.3,49,3.2,24.7
130,59.6,12,43.1,9.7
131,0.7,39.6,8.7,1.6
132,265.2,2.9,43,12.7
133,8.4,27.2,2.1,5.7
134,219.8,33.5,45.1,19.6
135,36.9,38.6,65.6,10.8
136,48.3,47,8.5,11.6
137,25.6,39,9.3,9.5
138,273.7,28.9,59.7,20.8
139,43,25.9,20.5,9.6
140,184.9,43.9,1.7,20.7
141,73.4,17,12.9,10.9
142,193.7,35.4,75.6,19.2
143,220.5,33.2,37.9,20.1
144,104.6,5.7,34.4,10.4
145,96.2,14.8,38.9,11.4
146,140.3,1.9,9,10.3
147,240.1,7.3,8.7,13.2
148,243.2,49,44.3,25.4
149,38,40.3,11.9,10.9
150,44.7,25.8,20.6,10.1
151,280.7,13.9,37,16.1
152,121,8.4,48.7,11.6
153,197.6,23.3,14.2,16.6
154,171.3,39.7,37.7,19
155,187.8,21.1,9.5,15.6
156,4.1,11.6,5.7,3.2
157,93.9,43.5,50.5,15.3
158,149.8,1.3,24.3,10.1
159,11.7,36.9,45.2,7.3
160,131.7,18.4,34.6,12.9
161,172.5,18.1,30.7,14.4
162,85.7,35.8,49.3,13.3
163,188.4,18.1,25.6,14.9
164,163.5,36.8,7.4,18
165,117.2,14.7,5.4,11.9
166,234.5,3.4,84.8,11.9
167,17.9,37.6,21.6,8
168,206.8,5.2,19.4,12.2
169,215.4,23.6,57.6,17.1
170,284.3,10.6,6.4,15
171,50,11.6,18.4,8.4
172,164.5,20.9,47.4,14.5
173,19.6,20.1,17,7.6
174,168.4,7.1,12.8,11.7
175,222.4,3.4,13.1,11.5
176,276.9,48.9,41.8,27
177,248.4,30.2,20.3,20.2
178,170.2,7.8,35.2,11.7
179,276.7,2.3,23.7,11.8
180,165.6,10,17.6,12.6
181,156.6,2.6,8.3,10.5
182,218.5,5.4,27.4,12.2
183,56.2,5.7,29.7,8.7
184,287.6,43,71.8,26.2
185,253.8,21.3,30,17.6
186,205,45.1,19.6,22.6
187,139.5,2.1,26.6,10.3
188,191.1,28.7,18.2,17.3
189,286,13.9,3.7,15.9
190,18.7,12.1,23.4,6.7
191,39.5,41.1,5.8,10.8
192,75.5,10.8,6,9.9
193,17.2,4.1,31.6,5.9
194,166.8,42,3.6,19.6
195,149.7,35.6,6,17.3
196,38.2,3.7,13.8,7.6
197,94.2,4.9,8.1,9.7
198,177,9.3,6.4,12.8
199,283.6,42,66.2,25.5
200,232.1,8.6,8.7,13.4