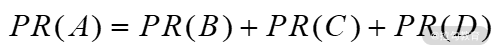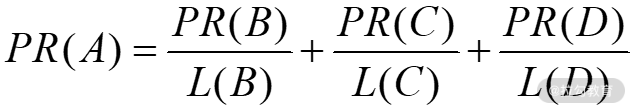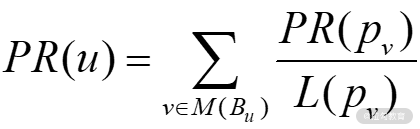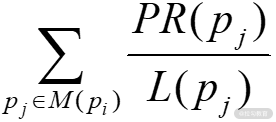大数据Spark实战第六集 图像处理和GraphX实战
什么是图:图模式,图相关技术与使用场景
在本模块中,我们将学习 Spark 如何处理图,也就是 Spark 的图挖掘套件 GraphX。虽然图这种数据结构在最近几年中,越来越多地出现在业务场景中,但平心而论,图的使用频率相比前面所学的内容还没有那么频繁。但是,一旦有这方面的需求,无论是工程师还是科学家,都可以用 Spark 提供的解决方案很好地完成任务,甚至可以说是“屠龙技”也不为过,经过本模块的学习之后,相信你也会有这样的感受。
本课时主要围绕图这种核心结构介绍,分为以下三个部分:
-
图结构
-
图存储
-
图相关计算场景和技术
图结构
图是一种较线性表和树更为复杂的数据结构,线性表和树分别表现的是一对一和一对多的关系,而图则表达的是多对多的关系。如下图所示,G1 是一个简单的图,其中 V1、V2、V3、V4 被称作顶点(Vertex),任意两个顶点之间的通路被称为边(Edge),它可以由(V1、V2)有序对来表示,这时称 G1 为有向图,意味着边是有方向的,若以无序对来表示图中一条边,则该图为无向图,如 G2。
在 G1 中,与顶点相关联的边的数量被称为顶点的度(Degree)。其中,以顶点为起点的边的数量被称为该顶点的出度(OutDegree),以顶点为终点的边的数量被称为该顶点的入度(InDegree)。
以 G1 中的 V1 举例,V1 的度为 3,其中出度为 2,入度为 1。在无向图 G2 中,如果任意两个顶点之间是连通的,则称 G2 为连通图(Connected Graph)。在有向图中 G1 中,如果任意两个顶点 Vm、Vn 且 m ≠ n,从 Vm 到 Vn 以及从 Vn 到 Vm 之间都存在通路,则称 G1 为强连通图(Strongly Connected Graph)。任意两个顶点之间若存在通路,则称为路径(Path),用一个顶点序列表示,若第一个顶点和最后一个顶点相同,则称为回路或者环(Cycle)。
图存储
由于图的结构比较复杂,所以无法存储在顺序映像的存储结构中,本课时中,我将为你介绍常用的几种图存储结构。
邻接矩阵
邻接矩阵是表示顶点之间相邻关系的矩阵。一般用二维数组存储,若图有 n 个顶点,则矩阵大小为 n * n,下面我用邻接矩阵来表示 G1、G2 :
其中矩阵的行标为起点,列标为终点。可以看到无向图必为对称矩阵,这一点可以在存储时进行优化。
邻接表
邻接表表示图的一种链式存储结构,在邻接表中,会对每个顶点建立一个单链表,每个单链表中保存了所有依附于该顶点的边,每个单链表中的结点由三个域组成:邻接点域、链域和数据域。其中,邻接点域指向与该顶点相邻的顶点,链域指向下一个与该顶点相关联的顶点,数据域保存了边相关的属性信息。用邻接表来表示 G1 ,则如下图所示:
对于无向图,V1 链表的结点个数就是 V1 的度数。而对于有向图来说,则只是 V1 的出度,如果想统计入度,则比较麻烦,需要遍历整个图。这种情况,可以通过建立一个逆邻接表来解决。在逆邻接表中,链域保存的是指向该顶点的下一个顶点,G1 的逆邻接表如下图所示:
如果是无向图 G2,邻接表则如下图所示:
邻接多重表
虽然邻接表是一种很有效的存储结构,但对于无向图来说,当同一条边(Vm、Vn)存在于第 m 个链表与第 n 个链表中时,对于修改图来说并不是特别方便。因此,进行这一类操作的无向图一般采用邻接多重表。在邻接多重表中,分为两个表:顶点表和边表,边表结构如下所示:
其中,mark 为标志域,可以用来标记该条边是否被搜索过;ivex 和 jvex 为该条边的起点和终点,ilink 指向下一条顶点 ivex 的出边;jlink 指向下一条以顶点 jvex 的入边,info 保存和边相关的信息,顶点表结构如下所示。
其中,data 域保存了和该顶点相关的信息,firstedge 域指向该顶点的第一条出边,下图中是 G2 以邻接多重表的形式进行存储:
比较流行的 Neo4j 图数据库就是采取邻接多重表的结构保存数据的。
十字链表
邻接表只体现了出度,虽然我们可以用逆邻接表来弥补入度信息,但是否存在一种将邻接表和逆邻接表结合起来的数据结构呢?这就是十字链表。十字链表分为顶点表和边表这两个表。边表结构如下所示:
其中 tailvex 和 headvex 为边的起点和终点,hlink 指向下一条顶点 tailvex 的出边;tlink 指向下一条以headvex为顶点的入边,顶点表结构如下所示:
其中 data 域保存了和该顶点相关的信息,firstIn 和 firstOut 是两个指针域,分别指向该顶点的第一条入边和第一条出边,如下图所示,该结构代表 G2 以十字链表的形式存储:
十字链表与邻接多重表的不同之处在于顶点表多了表示第一条入边的指针域。
边集数组
边集数组是一种利用一维数组存储图中所有边的图表示方法。该数组中每个元素都用来存储一条边的起点、终点(对于无向图,可选定边的任一端点为起点或终点)和边属性。此外,边集数组通常包括一个边数组和一个顶点数组。这种方式非常适合将数据进行分区,所以 GraphX 以及很多图数据库都采取这种方式存储数据。
图相关计算场景和技术
图面对的计算场景与普通的数据处理场景类似,主要可以分为 3 类:
-
OLTP
-
OLAP
-
离线处理
OLTP 和 OLAP 对应事务和分析场景,这两类场景通常由图数据库负责,它的特点是对实时性要求很高,比如在图中新增若干顶点并新增与之相连的边,这属于事务。再比如,查询以某个顶点为中心的,三度以内的顶点,这属于查询。这两类操作目前主流的图数据库都能很好地完成。
Neo4j 与 Cypher
Neo4j 是一个比较老牌的开源图数据库,目前在业界的使用也较为广泛,它提供了一种简单易学的查询语言 Cypher。Neo4j 采取类似于邻接多重表的数据结构存储数据,查询与插入速度较快,但由于没有分布式版本,图容量有限,而且一旦图变得非常大,如数十亿顶点,数百亿边,查询速度将变得缓慢。Neo4j 分为社区版和企业版,企业版有一些高级功能,但需要授权,非常昂贵,动辄数十万一年。
Apache TinkerPop与 Gremlin
TinkerPop 是一个开源的、面向集成的图计算框架,它包含一系列的组件,上图中每一个卡通形象都代表一个组件,分别是:Blueprints、Pipes、Frames、Furnace、Rexster 和 Gremlin。
中间的小人代表 Gremlin,它是 TinkerPop 的图查询语言,所有支持 TinkerPop 的系统都可以互相集成,例如原生的 TinkerPop 是用内存作为图存储,这无疑达不到生产环境的标准。你可以使用 MySQL 作为存储,也可以使用 NoSQL 分布式数据库,如 Cassandra、HBase、BerkeleyDB 等。索引也可以采用 Elasticsearch 或者 Lucene。使用 NoSQL 数据库作为存储引擎,只是实现了存储分布式,解决了图容量问题,但是没有实现查询分布式,使用 NoSQL 数据库作为存储引擎的产品有 Titan、JanusGraph。
TinkerPop 的核心是集成,如下图所示,用户可以根据自己需要,选择不同的组件,博采众家之长,并实现 TinkerPop 要求的标准,从而构建出一个图数据库,从这个意义上来说,TinkerPop 确实不单是一个数据库,而是一个框架。
值得一提的是,和关系型数据库一样,得益于社区和资本的助力,国产图数据库的发展也非常快,TigerGraph、Nebula 也非常值得你关注。
再来看看离线处理,这类场景通常代表一些比较复杂的分析和算法,如基于图的聚类,PageRank 算法等,这类计算任务对于图数据库来说就很难胜任了,主要由一些图挖掘技术来负责,这里我列出了两个比较常见的技术类型:
Pregel
Pregel 是 Google 于 2010 年在 SIGMOD 会议上发表的《Pregel: A System for Large-Scale Graph Processing》论文中提到的海量并行图挖掘的抽象框架,Pregel 与 Dremel 一样,是 Google 新三驾马车之一,它基于 BSP 模型(Bulk Synchronous Parallel,整体同步并行计算模型),将计算分为若干个超步(super step),在超步内,通过消息来传播顶点之间的状态。Pregel 可以看成是同步计算,即等所有顶点完成处理后再进行下一轮的超步,它的代表作就是 Spark 基于 Pregel 论文实现的海量并行图挖掘框架 GraphX,类似的还有 Yahoo 基于 MapReduce 实现的 Giraph 框架。
NetworkX
NetworkX 是一个用 Python 语言开发的图论与复杂网络建模工具,内置了常用的图与复杂网络分析算法,可以很方便地进行复杂网络数据分析、仿真建模等工作。用 NetworkX 可以很轻易地计算出基于图的一些指标和特征,这在传统方法中是非常困难的。NetworkX 与 GraphX 都是图计算工具。不同的是,GraphX 偏向于超大规模的图处理,例如千万顶点级别,而 NetworkX 处理的数据规模通常在百万顶点以内,十万顶点以内的图,算法效率最好。
GraphX 与 NetworkX 相比,最主要的区别在于处理数据的容量,GraphX 处理的数据量可以随着计算能力的增加而线性增长,十亿百亿顶点规模的图对于 GraphX 来说不在话下,但是由于 NetworkX 是单机计算包,所以图的容量最好不要超过百万顶点。此外,NetwrokX 对算法的封装程度很高,开箱即用,GraphX则更加底层。
小结
由于图结构的特殊性,没有接触过的同学未免会对这个概念有些陌生,本课时主要讲解了图存储和相关计算场景和对应的技术类型,主要是为后面的学习做铺垫,值得注意的是,图存储中介绍的 5 种数据结构非常底层,后面提到的技术对于图数据本身的存储无外乎这几种。
这里给你留一个思考题:
前面提到,Neo4j 采用的是邻接多重表作为自己的存储结构,那么 Tinkerpop 采用的是哪种存储结构呢?它们各自又有哪些优点呢?
数据并行:Spark 如何抽象图,如何切分图,如何处理图
GraphX 与 Spark 其他套件相比相对独立,拥有自己的核心数据结构与算子,本课时的主要内容有三个部分:
-
GraphX 核心数据结构
-
GraphX 图分区
-
GraphX 图算子
GraphX 核心数据结构
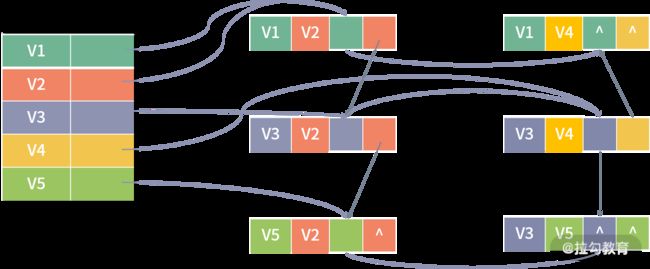
GraphX 用属性图的方式表示图,顶点有属性,边有属性。存储结构采用的是上一课时中介绍的边集数组的形式,即一个顶点表,一个边表,如下图所示。
其中,顶点 ID 是非常重要的字段,它不光是顶点的唯一标识符,也是描述边的唯一手段。顶点表与边表实际上就是 RDD,它们分别为 VertexRDD 与 EdgeRDD。在 Spark 的源码中,Graph 类如下:
abstract class Graph[VD: ClassTag, ED: ClassTag] protected () extends Serializable {
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
val triplets: RDD[EdgeTriplet[VD, ED]]
...
}
其中 vertices 为顶点表,VD 为顶点属性类型,edges 为边表,ED 为边属性类型,用户可以通过 Graph 的 vertices 与 edges 成员直接得到顶点 RDD 与边 RDD,顶点 RDD 类型为 VerticeRDD,继承自 RDD[(VertexId, VD)],边 RDD 类型为 EdgeRDD,继承自 RDD[Edge[ED]],triplets 表示边点三元组,如下图所示(其中圆柱形分别代表顶点属性与边属性):
通过 triplets 成员,用户可以直接获取到起点顶点、起点顶点属性、终点顶点、终点顶点属性、边与边属性信息。triplets 的生成可以由边表与顶点表通过 ScrId 与 DstId 连接而成。GraphX API 的开发语言目前仅支持 Scala。从上面的内容可以看出,GraphX 的核心数据结构 Graph 就是由 RDD 封装而成。
生成 GraphX 的 Graph 对象
想要生成 GraphX 的 Graph 对象,主要有以下两种方法:
-
从已有数据中生成
从已有数据中生成 Graph 对象主要分两大类:第一类是用 Graph 类的伴生对象方法,第二类是用 GraphLoader 类的 edgeListFile 方法。下面我将分别对其进行讲解:
1. Graph 伴生对象的方法
Graph 类的伴生对象方法如下:
def apply[VD: ClassTag, ED: ClassTag](
vertices: RDD[(VertexId, VD)],
edges: RDD[Edge[ED]],
defaultVertexAttr: VD = null.asInstanceOf[VD],
edgeStorageLevel: StorageLevel = StorageLevel.MEMORY_ONLY,
vertexStorageLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]
该方法调用方式如下:
val verteces: RDD[(VertexId, VD)] = ……
val edges: RDD[Edge[ED]] = ……
val defaultVerteces: VD = ……
val graph: Graph[VD,ED] = Graph(verteces, edges,defaultVerteces)
VertexId 是长整型。这是一种相对完善的生成图的方法,有顶点表、边表。此外,顶点与边的属性均可由数据得到。方法如下:
def fromEdgeTuples[VD: ClassTag](
rawEdges: RDD[(VertexId, VertexId)],
defaultValue: VD,
uniqueEdges: Option[PartitionStrategy] = None,
edgeStorageLevel: StorageLevel = StorageLevel.MEMORY_ONLY,
vertexStorageLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, Int]
从该函数的第一个参数即可看出,该方法针对的是用数字直接表示边与顶点的数据集,如下:
1 7
4 7
2 1
边属性值默认为 1,顶点默认属性值可以指定:
def fromEdges[VD: ClassTag, ED: ClassTag](
edges: RDD[Edge[ED]],
defaultValue: VD,
edgeStorageLevel: StorageLevel = StorageLevel.MEMORY_ONLY,
vertexStorageLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]
该方法从 RDD[Edge[ED]] 直接生成图,边属性由数据集提供,顶点默认属性值可以指定。
2. GraphLoader 的 edgeListFile 方法
GraphLoader 的 edgeListFile 方法如下:
def edgeListFile(
sc: SparkContext,
path: String,
canonicalOrientation: Boolean = false,
numEdgePartitions: Int = -1,
edgeStorageLevel: StorageLevel = StorageLevel.MEMORY_ONLY,
vertexStorageLevel: StorageLevel = StorageLevel.MEMORY_ONLY)
: Graph[Int, Int]
这种方法是由 GraphLoader 类提供的方法,与 fromEdgeTuples 方法类似,但不需要提供顶点默认属性值,顶点属性值与边属性值均默认为 1。
-
通过 GraphGenerators API 生成
前面主要介绍的是如何从已有数据生成 Graph 对象,在没有数据时,也可以用 GraphX 自带的 GraphGenerators API 生成符合某种规律的测试图数据。主要有下面几种类型的图:
基于度的图
下面这种方法生成的图,其顶点的度服从对数正态分布,可以通过参数指定顶点数、边分区数以及顶点的边数均值和标准差,最后一个是随机数种子,可以用当前的时间戳:
def logNormalGraph(
sc: SparkContext,
numVertices: Int,
numEParts: Int = 0,
mu: Double = 4.0,
sigma: Double = 1.3,
seed: Long = -1): Graph[Long, Int]
R-MAT 图
R-MAT 代表递归矩阵,通过下面这种方式模拟出来的图与社交网络结构类似:
def rmatGraph(
sc: SparkContext,
requestedNumVertices: Int,
numEdges: Int): Graph[Int, Int]
用上面两种方式生成的图就算参数一样,每次生成的结果也有可能不同。比如下面两种图,只要参数一样,每次生成的图就是一样的。
网格图
下面的方法会生成一个 rows×cols 的网格。网格中顶点的连接方式是一定的,上面的顶点指向下面的顶点,左边的顶点指向右边的顶点。
def gridGraph(
sc: SparkContext,
rows: Int,
cols: Int): Graph[(Int, Int), Double]
星形图
下面的方法会生成一个 1×nverts 的星形图(nverts 条边指向一个中心):
def starGraph(
sc: SparkContext,
nverts: Int): Graph[Int, Int]
GraphX 图分区
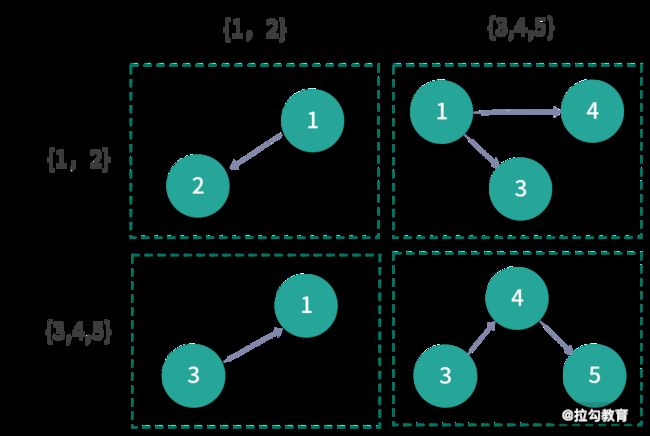
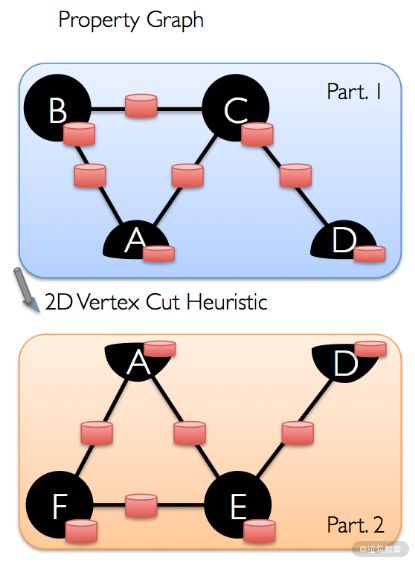
分区对于 RDD 来说是一个很重要的概念。它体现了并行的理念,是分布式计算的基础。对于普通 RDD 来说,分区的逻辑很简单,对数据集水平切分即可。但是在 GraphX 中,对 Graph 的分区就没那么简单了。对图进行分区,实际上就是对图进行切割,通常来说,有两种方式:边切割与顶点切割。如下图所示,左侧的两块图表示的是边切割,右侧的两块图表示的顶点切割。
在边切割中,边有冗余;在顶点切割中,顶点有冗余。与边切割相比,顶点切割可以减少通信与存储开销。你很容易发现,在 Graph 中的边表其实就是顶点切割的实现。所以在 GraphX 中,采取的是顶点切割的方式对图进行分区。而具体的每个分区包含哪些边,目前 GraphX 提供了 4 种分区策略:
-
EdgePartition1D;
-
EdgePartition2D;
-
RandomVertexCut;
-
CanonicalRandomVertexCut。
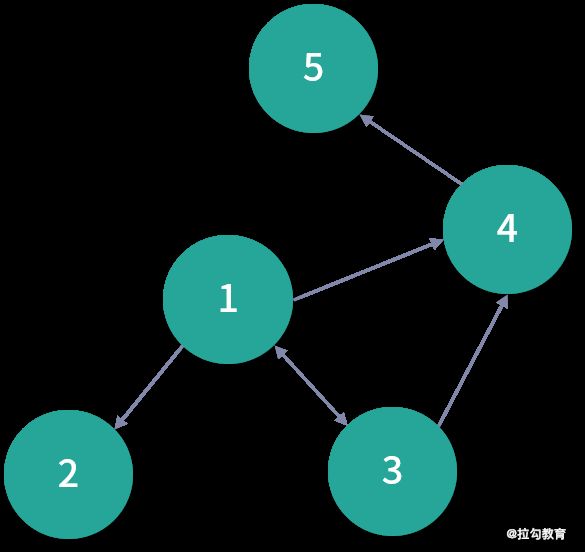
下面我就用一个例子来说明这几个分区策略的不同之处。假设原始图如下:
EdgePartition1D 分区策略保证了同一个顶点的出边一定在同一个分区中,如下:
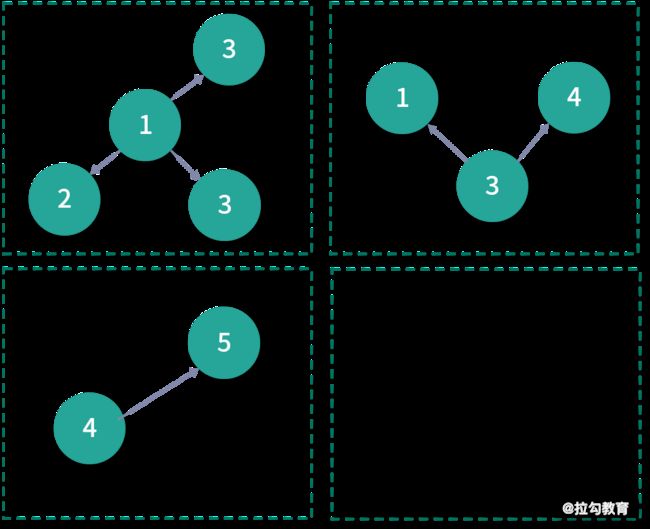
EdgePartition2D 分区策略将边表看成一个邻接矩阵,其中行标表示边的起点 ID,而列标则表示终点 ID,那么该邻接矩阵如下图所示:
其中 0 表示行标和列标对应的起点和终点不存在边,1 表示存在边。形象地说,分区就是对该矩阵进行分块(虚线所示)。按照上图的分块方式,EdgePartition2D 分区策略的边分布如下图所示:
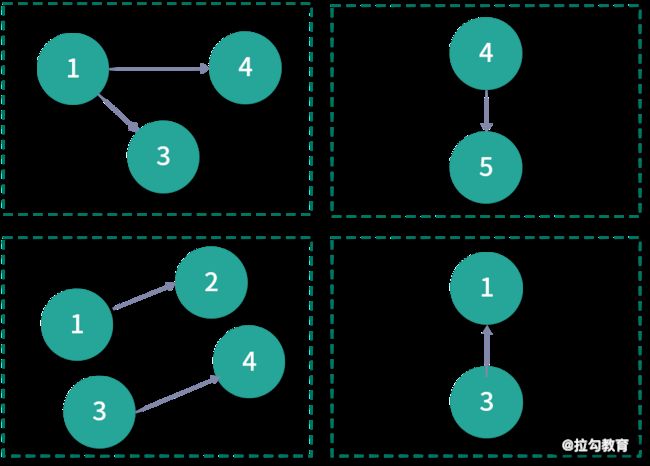
因此 EdgePartition2D 的分区数一定是个平方数。RandomVertexCut 的分区策略最为简单,就是对边表进行随机分区,这种方式可以实现边的完全负载均衡,但是对于度分布为幂律分布的图来说,很容易出现数据倾斜的问题,如下图所示:
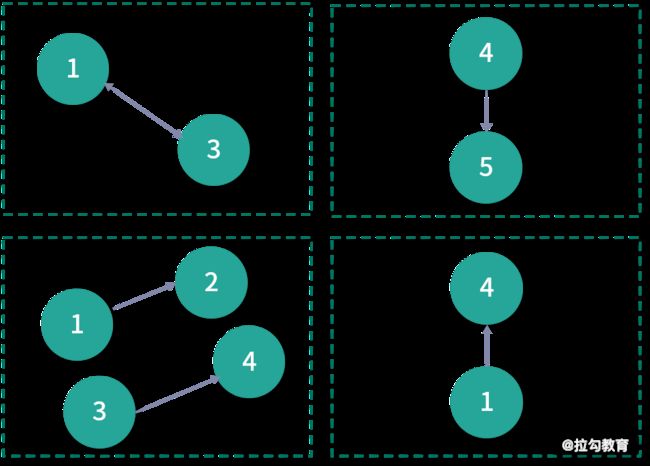
CanonicalRandomVertexCut 分区策略与 RandomVertexCut 类似,但它能保证两点之间的边在同一个分区,如下图所示:
确定好分区策略后,用户可以用如下代码对图分区策略进行设置:
...
val graph = Graph(nodes,edges)
graph.partitionBy(PartitionStrategy.CanonicalRandomVertexCut)
GraphX 图算子
作为有自己核心数据结构与分区策略的 GraphX,当然也有属于 Graph 独有的算子,不过这些算子平常的使用率并没有那么高。在学习了前面的内容后,相信你能够很快掌握这些算子。
属性算子
属性算子的主要作用是改变边的属性与顶点的属性。
-
def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]:将 VD 类型的顶点属性值变换为 VD2 类型的顶点属性值。
-
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]:将 ED 类型的边属性值变换为 ED2 类型的边属性值。
-
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]:将 ED 类型的边点三元组属性值变换为 ED2 类型的边点三元组属性值。
结构算子
该类算子可以改变整个图的结构。
-
def reverse: Graph[VD, ED]:reverse 算子会将图中所有边的起点与终点进行对调,再返回新生成的图。
-
def subgraph(epred: EdgeTriplet[VD,ED] => Boolean,vpred: (VertexId, VD) => Boolean): Graph[VD, ED]:subgraph 算子会根据传入的谓词表达式,分别对顶点与边进行过滤,然后再返回由剩下顶点与边组成的新图。这里,如果移除了点,那么与该点相连的边会断开。
-
def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]:返回和另一个图的公共顶点与边组成的图,类似于两个图求差集。
-
def groupEdges(merge: (ED, ED) => ED): Graph[VD,ED]:groupEdges 算子会合并相同起点与终点的边,并根据 merge 函数的逻辑生成新的边属性值。
连接算子
连接算子有以下几个。
-
def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD): Graph[VD, ED]:图本身的顶点表与一个新的顶点表做内连接,用户定义的 map 函数作用于连接上的顶点,生成新的顶点属性值。
-
def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2): Graph[VD2, ED]:图本身的顶点表与一个新的顶点表做外连接,用户定义的 map 函数作用于所有顶点,因此不仅需要处理连接上的顶点属性值合并的问题,还需要考虑如果没有连接上的情况。
图算子与 RDD 的算子类似,主要是对图进行一些简单而常用的变换。
小结
本课时的主要内容与前面模块的内容安排类似,和学习如何生成 RDD、RDD 算子一样,本课时的主要内容是学习如何生成 Graph、图算子等。
值得注意的是,Graph 与 RDD 一样,都比较底层,与 DataFrame 相对应,GraphX 也有基于DataFrame 的套件 GraphFrame,不过现在并没有加入 Spark 官方套件中,有兴趣的话,你可以试一试。
像顶点一样思考:大规模并行图挖掘引擎 GraphX
在前面的课时中,我们介绍了 Spark 如何抽象图、如何处理图,可能你会觉得有些奇怪,目前学到的这几个图算子离大规模并行挖掘似乎还很遥远,也没什么特别之处。其实,GraphX 真正的精华确实还没有学习到,而这也是本课时我将为你讲到的。
“像顶点一样思考”这句话来源于 Google 在 2010 年发表的一篇论文Pregel,Pregel 是为了纪念大数学家欧拉,著名的欧拉七桥问题提到的那条河就叫 Pregel。这篇论文提出了一种基于图的大规模并行处理思路,GraphX 可以认为是 Pregel 的开源实现。
GraphX 的 Pregel API 就是 Pregel 的开源实现,它完全继承了 Pregel 的思想,体现了一种不同的数据处理思路,本课时的内容有:
-
Pregel 的思想:像顶点一样思考
-
Pregel API
像顶点一样思考
在 Internet 出现后,互联网中的图规模越来越大,如网页之间的链接、社交网络等,这些网络动辄数十亿个顶点、数百亿条边,这对于高效处理这些图提出了新的挑战。Pregel 是一种为此而生的计算模型。在 Pregel 出现之前,要想实现一种处理大规模图数据的算法,需要面临以下几个选项:
-
构建一个定制化的基础架构需要大量工作,而每一种新算法与图都需要重复这些工作。
-
依赖已有的分布式计算平台,但它们通常不适合处理图,如 MapReduce,这类平台非常擅长处理海量结构化数据,但如果使用这类平台处理图数据,可能会造成性能和易用性方面的问题。这些平台对于 SQL 与聚合场景表现很好,但这些扩展对于更适合消息传递模型的图算法来说通常并不理想。
-
使用单点图算法库,如 NetworkX、JDSL、BGL、LEDA 等,但这类型库对于图规模大小有限制。
-
使用现有的并行图处理系统,如 BGL、CGMgraph,这类型类库虽然能够实现并行图算法,但并没有是实现容错性,或者其他对于超大规模分布式系统非常重要的特性。
Pregel 的目标是构建一个对于表达图算法足够灵活且可扩展与容错的平台,并提供其 API。Pregel 基于整体同步并行模型(Bulk Synchronous Parallel,BSP),计算过程包含一系列迭代,我们称其为超步(super step)。在每一个超步中,每个顶点会调用用户自定义函数。
用户自定义函数描述了顶点 V 的行为与单个超步 S。顶点 V 可以读取在超步 S−1 中发送给 V 的消息,并发送消息给其他顶点(这些信息会在超步 S+1 中被读取),然后再修改顶点 V 和它的出边的状态。通常来说,消息是沿着出边的方向发送,也可以通过指定顶点 ID 发送给特定顶点。
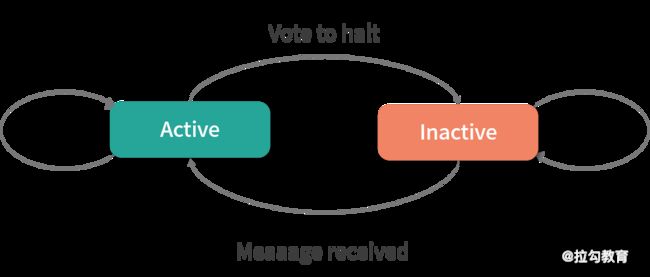
BSP 中同步的概念是指当所有顶点计算完成后,才会开始下一轮的迭代。在每个超步中,顶点会并行执行相同的用户自定义函数,这些用户自定义函数描述了整个图算法。算法停止的条件为每个顶点投票终止(Vote to halt),在第 0 个超步,所有顶点都是激活状态,所有激活的顶点都会参与到超步的计算中去。顶点通过投票终止来使自己不参与到计算中。这意味着:如果没有外部触发,该顶点就没有其他工作要做。直到该顶点收到一条消息,否则 Pregel 框架不会让该顶点参与到接下来的超步计算中去。
如果顶点是通过消息激活的,那么顶点必须显式地使自己进入未激活状态。整个算法停止的条件是所有顶点的状态为未激活,且没有消息在传递。顶点的状态机如下图所示:
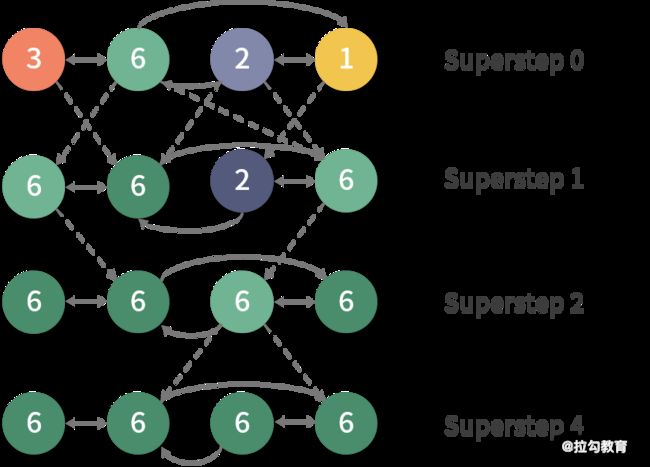
Pregel 计算模型对于表达图相关的算法表现力非常强,且更加自然,下图是一个简单的例子,实现的是强连通图的最值传播,可以帮助你加强对 BSP 模型的理解。
给定一个强连通图,每个顶点包含一个属性值。它将最大值传播到每个顶点。在每个超步中,任何更新了属性值的顶点都会再把消息发送给邻居顶点。当超步中没有顶点变化时,算法终止。上图中,虚线表示发送消息,灰色表示顶点投票终止。
Pregel API
GraphX 实现了 Pregel 计算框架,用户可以通过图算子的方式调用 Pregel API,如下:
def pregel[A: ClassTag](
initialMsg: A,
maxIterations: Int = Int.MaxValue,
activeDirection: EdgeDirection = EdgeDirection.Either)(
vprog: (VertexId, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED]
下面我来分别为你讲解各个参数的含义:
-
initialMsg:表示在最开始的超步中发送给所有顶点的初始消息,经常被用作初始化顶点的属性值;
-
maxIterations 为最大迭代次数,防止由于算法设计的原因,使程序陷入死循环;
-
activeDirection 为激活条件;
-
vprog、sendMsg、mergeMsg 都是用户自定义函数,它们会在一个超步中依次执行,用户需要在这 3 个函数中实现自己的图算法逻辑;
-
vprog 自定义函数:该函数是在每个超步中首先执行,从函数的声明也可看出,它的作用是,用接收到的消息与该顶点的属性值根据用户实现的逻辑得到新的顶点属性值;
-
sendMsg 自定义函数:该函数在 vprog 之后执行,返回的是一个消息的迭代子,其中元组的第一个元素为发送目的地顶点 ID;
-
mergeMsg 自定义函数:顶点会接收到多条消息,该函数是为了优化消息传输,对消息进行合并,该函数的输出会成为下一个超步中 vprog 的输入。
当所有消息停止传递且所有顶点投票终止时,Pregel 应用也就停止。activeDirection 参数设置的是消息发送的条件,该参数可以具体看成触发执行 sendMsg 的条件,它的值可以是以下几个:
-
EdgeDirection.Out:表示当边的起点顶点收到上一个超步的消息时,调用 sendMsg。
-
EdgeDirection.In:表示当边的终点顶点收到上一个超步的消息时,调用 sendMsg。
-
EdgeDirection.Either:表示当边的起点顶点或终点顶点收到上一个超步的消息时,调用sendMsg。
-
EdgeDirection.Both:表示当边的起点顶点和边的终点顶点收到上一个超步的消息时,调用 sendMsg。
经过 Pregel 计算模型地抽象,用户很多图挖掘算法都能很轻易地实现分布式,且 vprog、sendMsg、mergeMsg 对于图算法表现能力极强。用户实现这 3 个自定义函数时,视野中不再是整个图,更不是顶点表与边表,而是图中的一个个顶点与一条条边,这也是谷歌公司在 Pregel 论文最后提出的“像顶点一样思考(Think Like A Vertex)”的意义所在。
小结
本课时的内容虽然不是很长,但包含的内容非常丰富,在本课时中,我们提出了一种新思路,并将其实现。这种数据处理思路是很值得玩味的,并且对图的场景非常实用,如果你才刚接触,那么对于你来说确实有些距离感与新奇感。
为了帮助你尽快上手,这里留一个思考题:
如何求图中包含的三角形结构数?
你可以先试着用普通方法来完成,再试着用 Pregel API 实现。
为了降低难度,我这里给一个思路,可以试着实现:
如果顶点发送的某个消息经过三个超步后,刚好回到原点,那么可以认为是一个三角形结构。好了,就提示到这里。如果你还有问题的话,可以在留言区与我互动。
Pregel 还是 MapReduce:一个有趣的算子 AggregateMeage
在上一课时中,我们学习了 GraphX 的精髓:Pregel API 及其背后所蕴含的思想。你可能会发现,Pregel 和 MapReduce 模型差异很大,那么基于 MapReduce 的 Spark 和基于 Pregel 的 Graph 是否真有如此大的差别,它们是否存在某种共性?本课时将通过讲解 aggregateMessages 这个算子来回答这个问题。
aggregateMessages 是一个比较特殊的算子,它很少被直接使用,但却是 GraphX 的核心算子,是大规模并行图处理的基础,也是理解 Pregel 的关键所在。这个算子最大的特殊之处在于,从顶点的角度出发,用户可以通过该算子自定义 sendMsg 函数来使所有顶点沿着边,向边终点的顶点发送消息,再使用 mergeMsg 函数在目标顶点对收到的消息进行合并,最后返回一个新的顶点表,其中顶点属性的类型与消息类型相同,如下:
def aggregateMessages[Msg: ClassTag](
sendMsg: EdgeContext[VD, ED, Msg] => Unit,
mergeMsg: (Msg, Msg) => Msg,
tripletFields: TripletFields = TripletFields.All)
: VertexRDD[Msg]
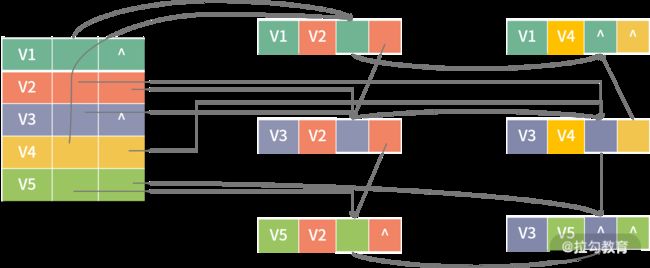
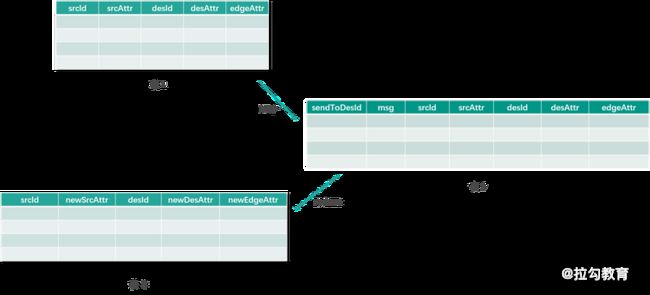
学习了上个课时的内容后,相信你已经能够理解消息传递的概念。sendMsg 接收 EdgeContext 类型的对象作为参数,该对象可以看成是一个边点三元组,即 triplet。通过该对象,用户可以得到起点顶点、终点顶点以及各自的属性(包括边),如下图中的表 1。
还可以利用 sendToSrc 与 sendToDst 向源顶点与目标顶点发送消息。用户可以通过 mergeMsg 函数来对消息进行合并。虽然 sendMsg 与 mergeMsg 的说法看起来比较新颖,有了拟物化的感觉,但其实可以将 sendMsg 看作是 MapReduce 模型中的 map 函数,而 mergeMsg 函数则可以看成是 reduce 函数,如下图所示:
上图表 1 中的每一行都会在 map 函数(sendMsg函数)的作用下,根据 srcAttr、desAttr、edgeAttr 生成待发送的消息 msg 和发送的目标顶点 Id(sendToDesId),中间结果(表 2)会根据目标顶点 Id(sendToDesId)进行分发,经过 reduce 函数(mergeMsg)的化简操作,得到最后的结果:具有全新属性值(newSrcAttr、newDesAttr、newEdgeAttr)的三元组表(表 3)。
这是一个简化的描述过程,但仍然可以看出 aggregateMessages 与 MapReduce 是非常相似的。事实上,aggregateMessages 上一个版本的名字更能说明问题——mapReduceTriplets,可以看到,这个算子的名字里面没有 Message 的字样,而是 MapReduce,说明这个算子和 MapReduce 模型有着很强的联系,而 mapReduceTriplets 的参数也印证了上图的过程:
def mapReduceTriplets[Msg](
map: EdgeTriplet[VD, ED] => Iterator[(VertexId, Msg)],
reduce: (Msg, Msg) => Msg)
: VertexRDD[Msg]
像上面讲到的那样,GraphX 通过顶点表与边表来生成图,这也是 Graph 的底层数据,因此,要想得到上图中的表 1,也就是边点三元组表,需要将原始顶点表与边表进行连接操作。
在上面的例子中,其实并不需要 desAttr(目标顶点属性)这个字段,所以在生成上图中的表 1 时,可以进行优化。aggregateMessages 的最后一个参数,可以指定用户需要哪一边顶点的属性值:源顶点、目标顶点或者二者都需要。默认为 TripletFields.All,那么这里用户的选择如下:
TripletFields.Src、
TripletFields.Dst、
TripletFields.All、
TripletFields.None
因此该字段的主要作用是对连接策略进行优化,它直接影响了连接的条件。如果图中有孤立的顶点,那么最后的结果中是不会包含这些顶点的。这也比较好理解,因为它们根本就没有出现在表 1 中。
综上所述,整个 aggregateMessages 算子可以拆分为 3 步,即连接(join)、转换(map)和化简(reduce),本课时一开始对于 aggregateMessages 算子的描述(顶点沿着边发送消息)看起来不好理解,但拆分成 3 步后,其实是再简单不过的操作的组合,只是换了个说法。
从这个层面上来说,Pregel 是基于 MapReduce 的计算模型,只不过声明的方式(编程接口)有所不同。
连接(join)、转换(map)和化简(reduce)这 3 步也刚好是 aggregateMessages 3 个参数的作用。从这 3 步可以看出,其中性能消耗比较大的是第 1 步连接操作,那么 aggregateMessages 的优化问题,其实又变成了连接问题的优化。
利用该算子,用户可以很容易地求得图中每个顶点的度数(入度和出度),以及每个顶点的邻居顶点。这些 GraphX 已经实现,用户直接调用即可。
aggregateMessages 算子的第一步是连接操作,也是性能消耗最大的一步。如果按照最原始的办法使用顶点表与边表直接进行散列连接,无疑会有很大性能问题。GraphX 对此有自己的优化方案。
首先,像前面介绍的一样,在对数据的分区上,就针对图进行了优化,每个分区内都会有一定数量的边。接下来 GraphX 会生成顶点与分区的路由表,其中路由表结构大致可看成List[(PartitionId,VertexIdList)]。
通过该路由表,可以得到每个分区中需要哪些顶点属性信息,这样就可以通过 Graph 内部维护的索引快速找到对应的顶点属性值,完成连接操作。这种操作类似于 Map 端连接,相当于每个图分区和一个顶点表的子集进行连接操作。但这样保证了这个顶点表正好包含了该图分区的所有顶点,因此不会影响结果的正确性。这也是 aggregateMessages 对于连接优化问题给出的答案,如下图所示:
小结
经过本课时的学习,你会发现 Pregel API 与 aggregateMessages 算子很像,aggregateMessages 也有sendMsg、mergeMsg 等参数,只是没有迭代的概念。事实上它们之间的关系是,Prege API 底层依赖的是 mapReduceTriplets,而 aggregateMessages 则是 mapReduceTriplets 的升级版,其中原理大致一样。
目前 Pregel API 实现仍然没有采用 aggregateMessages,虽然 aggregateMessages 相对 mapReduceTriplets 来说有较大性能提升。这也侧面说明 GraphX 其实是 Spark 中发展比较缓慢的模块,但是这并不影响 GraphX 在图计算场景中发挥的重要作用。
这里给你留一个思考题:连接的优化其实和我们前面讲到过的一种连接方式非常接近,是哪一种呢?
实战 1:用 GraphX 实现 PageRank 算法
在开始之前,我们先对上个课时的习题进行讲解,连接的优化其实和我们前面讲到过的一种连接方式非常接近,那就是 mapjoin。你答对了吗?如果有问题,欢迎和我在留言中讨论。
在前面的课程中,我们已经完整学习了 GraphX 的所有内容,并且对 Pregel API 也有了深入了解。本课时将会用 GraphX 实现 PageRank 算法,实践前面学到的内容。
PageRank 是谷歌公司创始人拉里佩奇和谢尔盖布林提出的链接分析算法,也被评为数据挖掘十大算法之一,它是用于计算网页重要性的基础算法。PageRank 算法会赋予每个网页一个分值,我们称之为** PR 分**,是用来衡量网页重要性的依据,值越大表示网页越重要,即越受欢迎。
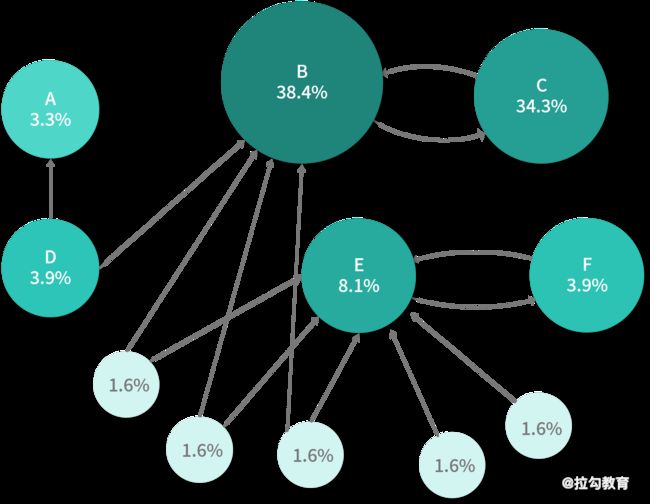
像谷歌这样的搜索引擎公司会泛爬全网所有公开网页,爬下来的网页会将自己的 URL 作为唯一标识进行存储,而网页中又有可能链接到其他网页,这样的数据天然就是图结构,网页就是图中的顶点,而边则是网页与网页之间的链接关系,如下图所示:
PageRank 本质上是计算图中顶点重要性的算法,这其实属于复杂网络中的中心性课题,在 PageRank 之前,其实也有人提出过用顶点的度来衡量,也就是简单地认为顶点的度越大,节点越重要,这其实就是度中心性(Degree Centrality),而 PageRank 计算的结果,我们也可以将其称为 PageRank 中心性。与度中心性不同的是,PageRank 除了考虑网页的链接数,还会考虑网页本身的质量,并将两者进行有机地结合。
PageRank 会用算法输出一个概率分布,用来表示随机点击链接的人将会到达任意特定页面的可能性。在计算过程开始时,假定图中所有网页的初始 PR 值相同。PageRank 需要多次迭代完成计算,通过迭代来调整近似的 PR 值,以更贴近反映理论的真实值。
概率为介于 0 和 1 之间的数值,通常,0.5 的概率表示为发生事件的概率为 50%。因此,0.5 的 PR 值意味着有 50% 的概率点击一个随机链接将被引导到该网页。
PageRank 若一开始假设每个网页的初始 PR 值为 0.25,在一次迭代中,给定网页的 PR 值会沿着出边将 PR 值进行传递,传输的值会根据出边的个数进行平均分配。如下图所示:
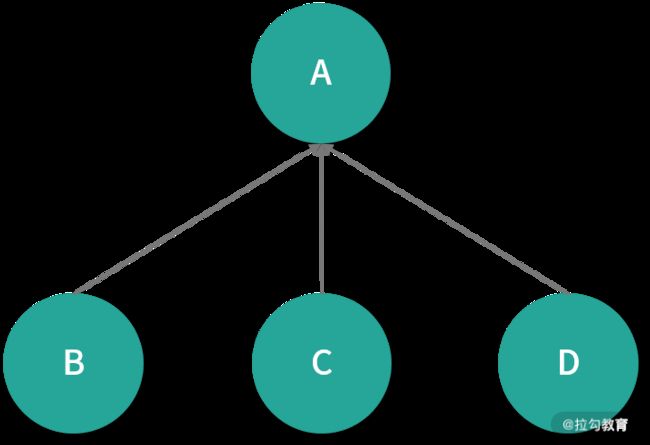
这个简单的图由网页 A、B、C、D 组成,图中链接除了 B、C、D 链向 A 以外,没有其他链接,那么在下一次,迭代 A 的 PR 值为 0.75,它的计算公式如下:
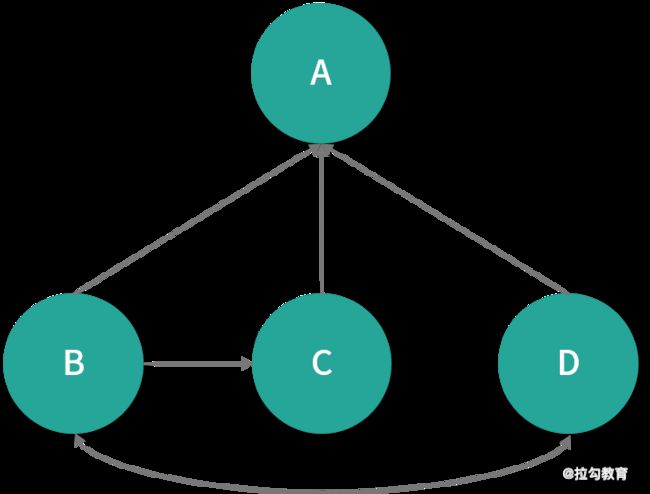
假设有另一种情况:B 链 向 C 和 A,C 链向 A,D 链向 A、B、C,如下图所示 :
在下一次迭代时,B 只会将自己 PR 值的一半(也就是 0.125)分别传送给 *A *和 C,而 *C *会将自己所有的 PR 值(也就是0.25)传输给自己链向的唯一页面 A。D 链向其他 3 个网页,所以传输给 3 个网页的值大概是 0.083。这样在下一次迭代完成后,A 的 PR 值大概为 0.458,计算公式如下:
换句话说,该网页赋予其他网页的值等于自己的 PR 值除以该网页的链出数 L,这样一来 PR(A) 可以表示为:
推而广之,任意网页 u 的 PR 值为:
即网页 u 的 PR 值等于,包含在集合 Bu(包含链入网页 u 的所有网页的集合)中每个网页 v 的 PR 值,除以相应网页 v 的链出数量 L(v) 的和。
PageRank 理论认为用户在随机点击网页的过程中,最终还是会停止点击的(如将网页加到收藏夹并退出,或者没有链出网页可点)。那么在每一步迭代中,用户还能继续点击的概率为 d,我们也称其为阻尼因子(damping factor),很多研究表明,该值大约在 0.85 左右。有了阻尼系数的 PR 值公式为:
这个公式采用的是一个随机网上冲浪者模型,用户在几次点击后感到无聊,并且切换到了一个随机页面,PageRank 的值在前面也提到过,反映了随机点击链接的人将会到达任何特定页面的可能性。这可以理解为马尔科夫链,状态就是下图中的页面,而转移概率就是页面之间的链接,是等可能的。换言之,用户点击页面的过程,是一个随机游走过程。
了解了 PageRank 算法后,我们发现这种算法很适合用 Pregel 编程模型来实现,其过程非常自然。事实上,谷歌公司也在论文中明确表示 PageRank 是由 Pregel 完成。作为图挖掘算法中最经典的算法之一,GraphX 也将其实现,源码文件可以在https://github.com/apache/spark/blob/master/graphx/src/main/scala/org/apache/spark/graphx/lib/PageRank.scala浏览并下载。
整个算法是由 runUntilConvergenceWithOptions 方法触发,在该方法中,首先会对图数据进行预处理:
...
// 用于设置后面的Personalized PageRank算法
val personalized = srcId.isDefined
val src: VertexId = srcId.getOrElse(-1L)
// 连接顶点度数与图
val pagerankGraph: Graph[(Double, Double), Double] = graph
.outerJoinVertices(graph.outDegrees) {
(vid, vdata, deg) => deg.getOrElse(0)
}
// 基于度数设置权重
.mapTriplets( e => 1.0 / e.srcAttr )
// 设置顶点属性为(0,delta)
.mapVertices { (id, attr) =>
if (id == src) (0.0, Double.NegativeInfinity) else (0.0, 0.0)
}
.cache()
其中 delta 用于记录两次迭代之间该顶点 PR 值的变化。下面就进入实现 PageRank 的 3 个核心函数,它们和pregel中的三个核心函数相对应:
def vertexProgram(id: VertexId, attr: (Double, Double), msgSum: Double): (Double, Double) = {
val (oldPR, lastDelta) = attr
// 此处resetProb = 0.15
val newPR = oldPR + (1.0 - resetProb) * msgSum
(newPR, newPR - oldPR)
}
def sendMessage(edge: EdgeTriplet[(Double, Double), Double]) = {
if (edge.srcAttr._2 > tol) {
Iterator((edge.dstId, edge.srcAttr._2 * edge.attr))
} else {
Iterator.empty
}
}
def messageCombiner(a: Double, b: Double): Double = a + b
这 3 个函数理解起来都比较容易,与前面介绍的 PageRank 并无二致。vertexProgram 函数计算新的 PR 值,并记录两次迭代产生的 PR 值之间的差异;sendMessage 函数根据链出边的权重生成发送对应顶点的消息(值)。注意,如果两次迭代的 PR 值足够小,将停止发送消息;messageCombiner 函数将会求出下面这个式子的值:
下面的代码将开始运行 PageRank 算法:
// 设定初始消息,其中Personalized PageRank的初始消息值为0
val initialMessage = if (personalized) 0.0 else resetProb / (1.0 - resetProb)
// 这里可以选取Twitter提出的Personalized PageRank实现,或者普通的PageRank实现
val vp = if (personalized) {
(id: VertexId, attr: (Double, Double), msgSum: Double) =>
personalizedVertexProgram(id, attr, msgSum)
} else {
(id: VertexId, attr: (Double, Double), msgSum: Double) =>
vertexProgram(id, attr, msgSum)
}
val rankGraph = Pregel(pagerankGraph, initialMessage, activeDirection = EdgeDirection.Out)(
vp, sendMessage, messageCombiner
)
.mapVertices((vid, attr) => attr._1)
// 归一化最后的PR值
normalizeRankSum(rankGraph, personalized)
这样我们就学习了 PageRank 算法,并用GraphX将其实现,本课时为实践环节,难度并不是很大。理解 PageRank 算法并不难,理解它的 Pregel API 实现也不是很难,难的是习惯用这种思维来表达算法,在遇到图的场景时,不妨多“像顶点一样思考”。
这里给你留一个课后作业:Personalized PageRank 和 PageRank 有什么不同?
实战 2:用 GraphX 求得顶点的 n 度邻居
在开始本课时的内容之前,我们先来回顾一下上个课时的习题:Personalized PageRank 和 PageRank 有什么不同?
个性化 PageRank(Personalized PageRank) 算法继承了经典 PageRank 算法的思想,利用数据模型(图)链接结构来递归地计算各结点的权重,即模拟用户通过点击链接随机访问图中结点的行为 (随机行走模型)计算稳定状态下各结点得到的随机访问概率。个性化 PageRank 与 PageRank 的最大区别在于随机行走中的跳转行为。
接下来,我们就进入本课时的学习。GraphX 内置了 collectNeighborIds 函数,可以得到每个顶点的邻居顶点,也就是 1 度邻居顶点。如果需要得到每个顶点的 2 度或者 n 度邻居顶点,应该如何利用 GraphX 完成这个任务呢?本课时将解答这个问题。
求 n 度邻居顶点要比 1 度邻居顶点更复杂一些,核心是要模拟出一个带有生命值的消息,每传播一次,生命值就会相应减 1,那么在生命值为 0 的时候到达的顶点就是我们所求的 n 度邻居顶点。
本课时将用 GraphGenerators 造出一个度分布为正态分布的图,然后实现 vertexProgress、sendMsg 和 mergeMsg 这 3 个关键函数,代码如下:
import org.apache.spark.graphx.EdgeTriplet
import org.apache.spark.graphx.EdgeDirection
import org.apache.spark.SparkConf
import org.apache.spark.SparkContext
import org.apache.spark.graphx.util.GraphGenerators
import org.apache.spark.graphx.VertexId
import org.apache.spark.graphx.PartitionStrategy
import org.apache.spark.graphx.Graph.graphToGraphOps
import scala.Iterator
object NDegreeNeighbor {
def main(args: Array[String]): Unit = {
// 顶点个数
val vextexNum = args(0).toInt
// 期望
val u = args(1).toDouble
// 方差
val sigma = args(2).toDouble
// 边分区数
val eParts = args(3).toInt
// 结果输出
val outputPath = args(4)
// 分区数
val numParts = args(5).toInt
// 分区策略
val partStra = args(6).toInt
// n
val n = args(7).toInt
val conf = new SparkConf()
conf.setAppName("NDegreeNeighbor")
val sc = new SparkContext(conf)
// 生成度分布为对数正态分布的图,并将顶点属性初始化
val g = GraphGenerators
.logNormalGraph(sc, vextexNum, eParts, u, sigma, System.currentTimeMillis())
.mapVertices[(List[Long],List[(Long,Int)],Int)]((x,y) => (List(),List(),0))
.partitionBy(
if(partStra == 0)
PartitionStrategy.EdgePartition1D
else if (partStra == 1)
PartitionStrategy.EdgePartition2D
else if (partStra == 2)
PartitionStrategy.CanonicalRandomVertexCut
else
PartitionStrategy.RandomVertexCut,numParts)
// 执行Pregel并保存结果
g.pregel[List[(Long,Int)]](List((-1L,-1)), n, EdgeDirection.Out)(vertexProgress, sendMsg, mergeMsg)
.vertices
.filter(x => if(x._2._1 == List()) false else true)
.saveAsTextFile(outputPath)
def vertexProgress(
id:VertexId,
attr:(List[Long],List[(Long,Int)],Int),
msgSum:List[(Long,Int)])
:(List[Long],List[(Long,Int)],Int) = {
// 迭代次数
val iteCount = attr._3
// 保存邻居顶点Id的集合
val neighbor = attr._1
// 消息存储(集合)
val msgStore = attr._2
// 新的迭代次数
val newIteCount = iteCount + 1
// 如果是第一次迭代
if(iteCount == 0){
(List(),List(),newIteCount)
// 如果是第n + 1次迭代,那么将生命值为1的消息保留
}else if(newIteCount == n + 1){
val newNeighbor = msgSum.par.filter(x => if(x._2 == 1) true else false).map(_._1).toList
(newNeighbor,List(),newIteCount)
// 将传过来的消息保存,生命值-1,以备下一次发送消息,再滤掉不可能跳5次的消息
}else{
val newMsgStore:List[(Long,Int)] = msgSum.map(x => (x._1,x._2 - 1)).++(msgStore)
.map(x => (x._1,x._2 - 1))
(List(),newMsgStore,newIteCount)
}
}
def sendMsg(edgeTriplet: EdgeTriplet[(List[Long],List[(Long,Int)],Int), Int]):Iterator[(Long,List[(Long,Int)])] = {
val oldMsg = edgeTriplet.srcAttr._2
val iteCount = edgeTriplet.srcAttr._3
// 最开始发消息,初始化生命值为n
if(iteCount == 1){
Iterator((edgeTriplet.dstId,List((edgeTriplet.srcId,n))))
}else{
Iterator((edgeTriplet.dstId,oldMsg.par.filter(x => if(x._2 + iteCount == n + 1) true else false).toList))
}
}
def mergeMsg(a:List[(Long,Int)],b:List[(Long,Int)]):List[(Long,Int)] = {
a.++(b)
}
}
}
其中,u、sigma 参数用来声明生成图的顶点数的期望与标准差(对数正态分布)。另外,核心的数据结构是消息的数据结构与顶点属性的数据结构,它们分别是 List[(Long,Int)] 和 (List[Long],List[(Long,Int)],Int),前者的消息是顶点 Id 以及消息生命值组成的元组。后者元组中的第一个元素是保存当前顶点的 n 度邻居顶点 Id 的集合,用于结果输出;第二个元素用于存储发送过来的消息,第三个元素是当前迭代次数。
在本例中,没有考虑成环的情况,你可以试着实现一下这种情况,这也是本课时留给你的思考题。
其实求顶点的 n 度邻居这个需求并不常见,之所以举这个例子,是因为它很好地体现了 Pregel API 的核心用法:消息传递。你可以仔细理解这个带有生命值的消息的抽象,如果有更好的方法,欢迎与我讨论。