西瓜书--第五章.神经网络
人工神经网络（ANN）：模拟人脑神经系统的结构和功能，运用大量简单处理单元经广泛连接而组成的人工网络系统。
一、神经元
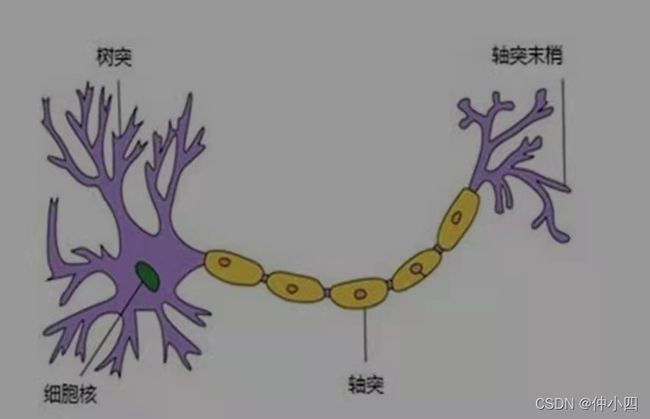
一个神经元通常具有多个树突。主要用来接收传入信息，而轴突只有一条。轴突可以给其他多个神经元传递信息。轴突末梢与树突产生连接，从而传递信号，这个连接则对应着一个权重；权重的值称为权值，这是需要训练得到的。即每个连接线对应一个不同的权重。
神经元模型是一个包含输入，输出与计算功能的模型。输入可以类比为神经元的树突，而输出可以类比为神经元的轴突，计算则可以类比为细胞核。神经网络中最基本的成分是神经元模型。
这里再次强调就是连接是神经元中最重要的东西，每一个连接上都有一个权重。
一个神经网络的训练算法就是让权重的值调整到最佳，以使得整个网络得预测效果最好。
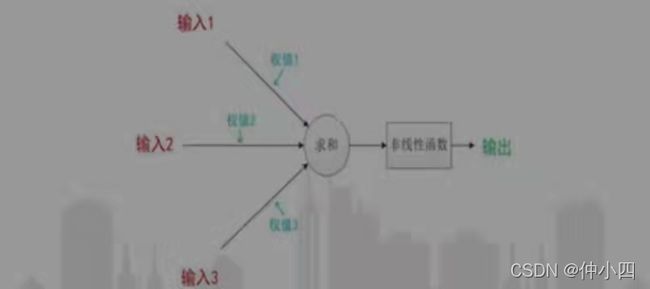
其中一直沿用至今的是M-P神经元模型。在这个模型中，神经元接收来自n个其他神经元传递过来的输入信号，这些输入信号通过权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理以产生神经元的输出。
接下来是关于神经元的计算，输入总共经历了三步数学运算：
1.先输入乘以权重（weight）：x1-->x1 * w1;x2-->x2 * w2
2.求和：(x1 * w1) + (x2 * w2) + b
3.经过激活函数处理得到输出：y = f((x1 * w1) + (x2 *w2) +b)
激活函数：
神经网络中引入非线性函数作为激活函数，它不再是输入得线性组合，而是几乎可以逼近任意函数。
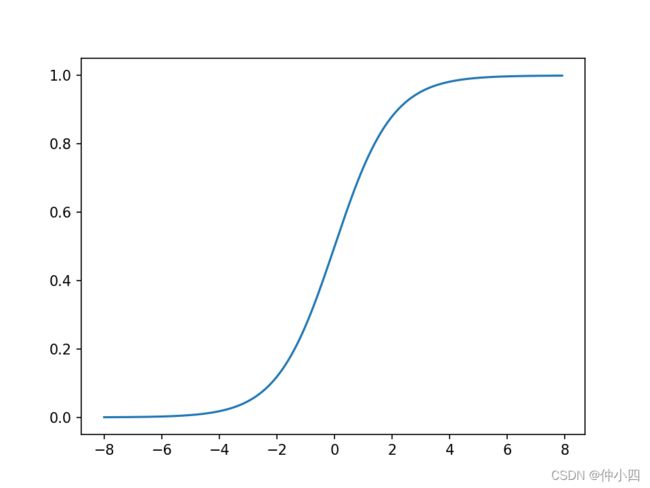
激活函数的作用：将无限制得输入转换为可预测形式得输出，常用得激活函数是sigmoid函数。
sigmoid函数把可能在较大范围内变化的输入值挤压到（0，1）输出值范围内，所以有时也称为”挤压函数“。
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(x):
# 直接返回sigmoid函数
return 1 / (1 + np.exp(-x))
def plot_sigmoid():
# param:起点，终点，间距
x = np.arange(-8, 8, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.show()
if __name__ == '__main__':
plot_sigmoid()
二、神经网络
多层次的神经网络，并不是 层次越多越好。
如何搭建神经网络：
1.搭建神经网络就是把多个神经元连接在一起。
2.这个神经网络有2个输入、一个包含2个神经元的隐藏层（h1和h2）、包含1个神经元的输出层o1。
3.隐藏层是夹在输入层和输出层之间的部分，一个神经网络可以有多个隐藏层。
三、感知机(参考《统计学习方法》)与多层网络
感知机由两层神经元组成。输入层接收外界输入信号后传递给输出层，输出层是M-P神经元，亦称”阈值逻辑单元“。
感知机是二分类问题的线性分类模型。单层感知机只能处理线性问题，无法处理非线性问题！！！感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元。要解决非线性问题，需要考虑使用多层功能神经元。输出层与输入层之间的一层神经元被称为隐含层或隐层，隐含层与输出层神经元都是拥有激活函数的功能神经元。
每层神经元与下一层神经元全互连，神经元之间不存在同层连接，也不存在跨层连接，这样的神经网络结构通常称为”多层前馈神经网络“。
输入层神经元仅仅是接收输入不进行函数超出了，隐层与输出层包含功能神经元，则称其为”两层网络“；只需包含隐层，即可称为”多层网络“。
四、误差逆传播算法（BP算法）
BP是一个迭代学习算法，在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计。
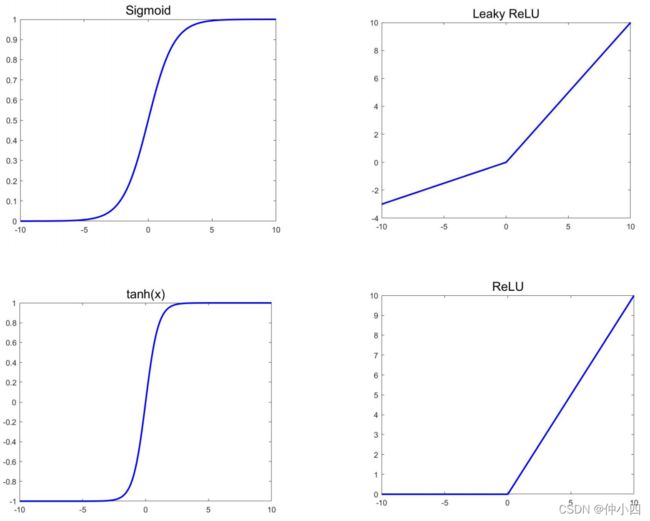
常见的激活函数选择：sigmoid函数、tanh函数、ReLU函数、Leaky ReLU函数。
算法流程：
import numpy as np
def mse_loss(y_true, y_pre):
# y_true 和 y_pre 是同样长度的np数组
return ((y_true - y_pre) ** 2).mean()
测试代码：
y_true = np.array([1, 0, 0, 1])
y_pre = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pre)) # 0.5第六章-支持向量机(SVM)
http://t.csdn.cn/q6o2F
http://t.csdn.cn/q6o2F第四章-决策树http://t.csdn.cn/3Tme3http://t.csdn.cn/3Tme3第三章-线性模型http://t.csdn.cn/4S6Y6http://t.csdn.cn/4S6Y6