文献阅读21期：Attention mechanisms and deep learning for machine vision: A survey

[ 综述阅读·机器视觉 ] Attention mechanisms and deep learning for machine vision:
A survey of the state of the art

推荐理由：一篇较新的综述，主在介绍Attention和配套的深度学习机制在机器视觉领域的最新成果，作者把来龙去脉讲得较为明白，一篇好文

1.摘要&简介

• 最近几年，NLP领域较火的用于上下文预测识别的Attention机制获得了学界很大的认可，这引起了很多其他领域学者的注意。其中博主认为最主要的原因是，我们生活当中很多数据都是需要经过推理得来的，这就意味着很多“未知情况”的预测是需要根据已有的上下文来推理的。
• 而上述这种需求，简单来说，恰好是Attention所擅长的事情，只要对已有的数据进行恰当的Embedding就能实现相应功能。
• 基于以上这种思想，越来越多的计算机视觉领域专家也开始采用Attention机制。
• 博主说：很多Sequence或Query基础的运算，也可以通过Attention机制来处理，你比如VRP问题，RCPSP问题，这种有先后时序和序列输出的问题，都能采用类似的方法来训练并求解。

1.1.自注意力机制

• 自注意力机制旨在为序列中的每个元素建立一个专门用于关系预测的网络（不觉得某种网络跟其思想很像么？）
• 令一个含有n个实体的序列为$\left({\mathbf{x}}_1,{\mathbf{x}}_2,\dots {\mathbf{x}}_n\right)$ by $\mathbf{X}\in {\mathbb{R}}^{n\times d}$，其中d为embedding之后的维度大小。自注意的目的是在对整个语境知识中的每一个元素进行编码后，捕捉所有n个元素之间的依赖关系。
• 但完成上面这个过程，首先需要将一个序列转换为3中可学习的矩阵（是不是有点像CNN里的卷积核？哈哈！）：Queries $\left({\mathbf{W}}^Q\in {\mathbb{R}}^{n\times d_q}\right)$，Keys $\left({\mathbf{W}}^K\in {\mathbb{R}}^{n\times d_k}\right)$，Values $\left({\mathbf{W}}^V\in {\mathbb{R}}^{n\times d_v}\right)$。
• 有了上述三个卷积核，啊不对，三个特征提取权重矩阵后，对原始序列$\mathbf{X}$进行如下运算，得到三个矩阵（注意，非常重要，Attention的基础思想）：
  $$\mathbf{Q}=\mathbf{X}{\mathbf{W}}^Q,\mathbf{K}=\mathbf{X}{\mathbf{W}}^K\text{ and }\mathbf{V}=\mathbf{X}{\mathbf{W}}^V$$
• 有了上述三种预处理，那自注意力层的输出就可以表达为：
  $$Z=\mathrm{softmax}\left(\frac{\mathbf{Q}{\mathbf{K}}^T}{\sqrt{d_q}}\right)\mathbf{V}\text{\hspace{1em}(1)}$$
• 对于向量/序列中的某个元素，自注意机制从根本上找到查询与所有键的点积，然后通过softmax函数对该点积进行归一化，以获得注意图分数。现在每个元素都假定向量/序列中所有元素的加权和的值，其中所有权重都等于注意图得分。

1.2.带遮罩的自注意力机制

• 自注意力机制原本旨在对当前时间戳上的实体的预测提供“过去依据”，但如果将未来的元素当成当下的预测参考，肯定会造成一些不好的影响（想象一下，你从未来穿越回来告诉现在的自己该怎么做，那还不得乱套了？），增加Mask的Self-attention如下：
  $$\mathrm{softmax}\left(\frac{\mathbf{Q}{\mathbf{K}}^T}{\sqrt{d_q}}\circ \mathbf{M}\right)\text{\hspace{1em}(2)}$$
  其中，$\circ$是Hadamard积，在预测向量/序列中的一个元素时，在掩蔽的自我注意中，未来元素的注意图分数被设置为0。

1.3.多头注意力机制

• 虽然自注意力机制很好，但需要注意的是，元素之间的关系并不仅仅维系于“点到点”的层面，有时关系甚至会出现在“面到面”的层面（博主说人话：有时候一个句子里，不仅仅有字与字之间的关系，甚至有单词和单词的关系。在文章里，甚至有句子和句子的关系，在论文里，还有章节对章节的关系，这种层次化的关系，层层套娃，咱们需要一个套娃机来表示它。）
• 一般来说，多头注意过程由多个自我注意单元组成，在原始Transformer结构中h=8。
• 每个单元都由可学习权重矩阵构成：$\left\{{\mathbf{W}}^{Q_i},{\mathbf{W}}^{K_i},{\mathbf{W}}^{V_i}\right\}$。
• 对于一个输入序列$\mathbf{X}$，原本的注意力机制层的输出为$\mathbf{Z}$，但多头注意力机制就不止这一个Z了，它是一箩筐Z：$\left[{\mathbf{Z}}_0,{\mathbf{Z}}_1,\dots {\mathbf{Z}}_{\mathrm{h}-1}\right]\in {\mathbb{R}}^{n\times h\times d_v}$，而相应权重为：$\mathbf{W}\in {\mathbb{R}}^{h\cdot d_v\times d}$

2.基于注意力机制的深度学习结构

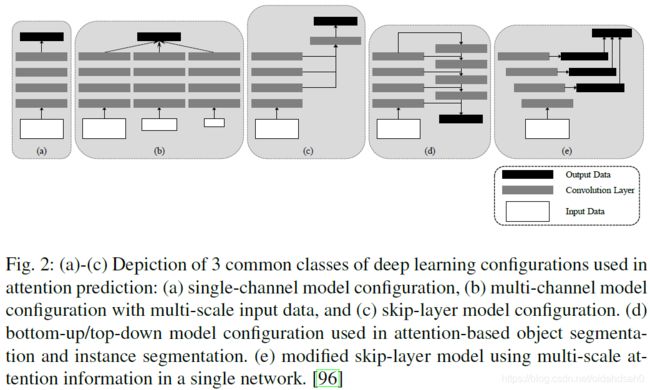
• 如上图所示，流行的深度注意模型的架构分为以下几个重要类：
  1. Single channel model
  2. Multi-channel model feeding on multi-scale data
  3. Skip-layer model
  4. Bottom-up/ top-down model
  5. Skip-layer model with multi-scale saliency single network

2.1.单信道模型（Single channel model）

• 单信道模型是各种基于CNN的注意模型的主要结构，也被许多基于注意的研究所采用。几乎所有其他类型的CNN配置都可以看作是单信道模型的变体。
• 研究表明，不同层次和尺度上的注意线索对注意力的影响是至关重要的。将CNNs的多尺度特征应用到基于注意的模型中是一个明显的选择。在下一种单通道模型，即多通道模型中，这些变化是沿着这条线进行的。

2.2.多信道模型（Multi-channel model）

• 多通道模型的基本概念如图2b所示。这种模型通过多尺度数据输入训练多个模型来学习多尺度注意信息。多个模型通道是并行的，可以具有不同比例的不同配置。输入数据通过多个通道同时传送，然后将不同通道的特征融合并传送到统一的输出层，生成最终的注意力图。我们观察到在多通道模型中，多尺度学习发生在个体模型之外。在接下来讨论的配置中，多尺度学习在模型内部，这是通过组合来自不同卷积层层次结构的特征映射来实现的。

2.3.跨层际模型（Skip-layer model）

• 图2c显示了中使用的一种常见的跳跃层模型。跳层模型不是从多尺度图像上的多个平行通道中学习，而是学习主通道中的多尺度特征图。多尺度输出从具有越来越大的接收场和下采样率的各个层学习。接下来，对这些输出进行融合，输出最终的注意力图。

2.4.自下而上/自上而下模型（Bottom-up/ top-down model）

• 这种相对较新的模型配置称为自顶向下/自下而上模型，已用于基于注意的对象分割和实例分割。模型的结构如图2(d)所示，其中首先通过常见的自下而上卷积技术获得分割特征图，然后进行自上而下的细化，以便将从深层到浅层的数据融合到掩模中。这种配置背后的主要动机是产生高保真分割掩模，因为深层CNN层会丢失精细的图像细节。自下而上/自上而下的模型类似于跳层模型，因为不同的层相互连接。

2.5.多尺度显著单网络跳层模型（Skip-layer model with multi-scale saliency single network）

• 图2(e)中所示的模型受深度监督模型的启发。该模型利用多层次、多尺度的基于注意的信息，通过深度监督技术进行学习。该模型与以前的模型的一个重要区别是前者提供了对隐藏层的组合直接监控，而不是只监控最后一个输出层，然后将监控的输出传播回以前的层。它利用了跳层模型2©的优点，即不从具有多尺度输入数据的多模型通道中学习。此外，它比多通道模型2(b)和自底向上/自顶向下模型2(d)更轻。研究发现，自底向上/自顶向下模型存在训练困难，而深度监督模型具有较高的训练效率。在下一节中，本文将对机器视觉中的各种注意机制和深度学习技术进行分类，并详细讨论每一类。

3.机器视觉中的注意力与深度学习

• 机器视觉中的注意力研究主要分为三大类：
  1. Attention-based CNNs
  2. CNN transformer pipelines
  3. Hybrid transformers

3.1.Attention-based CNNs

• 最近注意机制被应用于机器视觉应用的深度学习中，例如目标检测、图像字幕和动作识别。注意机制的核心思想是在卷积神经网络（CNNs）中定位特征映射中最显著的部分，以消除机器视觉应用中的冗余。
• 通常，注意力是通过使用注意力Map嵌入到CNN中的。
• 有的基于注意力Map的论文，以自学习的方式产生了其他信息，而对注意Map的监督很弱。
• 有的论文引用其他技术，通过利用人类注意力数据或通过关注感兴趣区域（ROI）来指导CNN。

3.1.1.图像分类检索与目标检测

• 人在看一张图的时候，肯定不可能把每一个像素都看进去，而是仅仅关注核心且突出的点。
• 直接从CBAM开始。对于输入的Feature Map：$\mathbf{F}\in {\mathbb{R}}^{C\times H\times W}$，CBAM给出一个1维的Attemtion Map：${\mathbf{M}}_c\in {\mathbb{R}}^{C\times 1\times 1}$以及一个2维的spatial attention map：${\mathbf{M}}_s\in {\mathbb{R}}^{1\times H\times W}$，如图3所示：
  
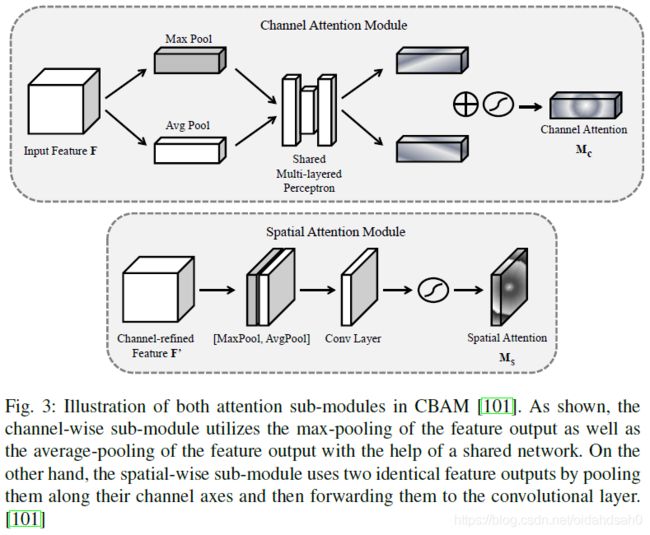
• 这种注意机制的运作可以表达为：
  $${\mathbf{F}}^{\prime }={\mathbf{M}}_c(\mathbf{F})⨂\mathbf{F}\text{\hspace{1em}(3)}$$
  $${\mathbf{F}}^{\prime \prime }={\mathbf{M}}_s\left({\mathbf{F}}^{\prime }\right)⨂{\mathbf{F}}^{\prime }\text{\hspace{1em}(4)}$$
  其中，$⨂$是元素到元素的乘法运算符。
• Channel注意力的数学计算如下：
  $$\begin{array}{rl}{\mathbf{M}}_c(\mathbf{F})=\sigma (\mathrm{MLP}(\text{ AvgPool }(\mathbf{F}))+& \mathrm{MLP}(\mathrm{MaxPool}(\mathbf{F})))\\ & =\sigma \left({\mathbf{W}}_1\left({\mathbf{W}}_0\left({\mathbf{F}}_{\text{avg }}^c\right)\right)+{\mathbf{W}}_1\left({\mathbf{W}}_0\left({\mathbf{F}}_{\max }^c\right)\right)\right)\end{array}\text{\hspace{1em}(5)}$$
  其中$\sigma$是sigmoid函数，且有${\mathbf{W}}_0\in {\mathbb{R}}^{C/r\times C}$和${\mathbf{W}}_1\in {\mathbb{R}}^{C\times C/r}$。多层感知权重(MLP)${\mathbf{W}}_0$和${\mathbf{W}}_1$，为所有输入所共享。${\mathbf{W}}_0$在经过ReLU激活后得出。即有：
  $${\mathbf{M}}_s(\mathbf{F})=\sigma \left(f^{7\times 7}([\mathrm{AvgPool}(\mathbf{F});\mathrm{MaxPool}(\mathbf{F})])\right)=\sigma \left(f^{7\times 7}\left(\left[{\mathbf{F}}_{\text{avg }}^s;{\mathbf{F}}_{\max }^s\right]\right)\right)\text{\hspace{1em}(7)}$$
• 对于AG-CNN：基于三种不同的监督Loss来训练：
  1. attention-prediction
  2. eature-visualization
  3. glaucoma-classification
• AG-CNN作者使用Kullbac-Leibler（KL）散度函数作为自然引起的注意力Loss的等价，其如下所示：
  $${\mathrm{Loss}}_a=\frac{1}{I\cdot J}\sum _{i=1}^I\sum _{j=1}^J{A}_{ij}\log \left(\frac{A_{ij}}{{\hat{A}}_{ij}}\right)\text{\hspace{1em}(7)}$$

3.1.2.手语识别

• 在手语识别中，空间注意的Map可以如下计算：
  $$M_{i,k}(p)=\exp \left(-\frac{{\Vert p-x_{i,k}\Vert }_2^2}{\sigma }\right)\text{\hspace{1em}(8)}$$

4.后续

• 后续部分都相对简单些，可以阅读原文。

参考文献

[1] Hafiz A M, Parah S A, Bhat R U A. Attention mechanisms and deep learning for machine vision: A survey of the state of the art[J]. 2021.