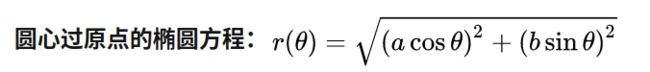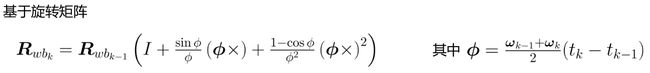【ORB_SLAM3源码解读】IMU基础介绍、IMU姿态、速度、位置解算以及误差方程、坐标系

ORB_SLAM3优势

IMU(Inertial Measurement Unit),惯性测量单元
• 典型 6 轴 IMU 以较高频率(≥ 100Hz)返回被测量物体的角速度与加速度
• 受自身温度、零偏、振动等因素干扰,积分得到的平移和旋转容易漂移

六自由度 IMU 本身由一个陀螺仪和一个加速度计组成,分别测量自身的角速度和加速度。

IMU 适合计算短时间、快速的运动;

快速响应,不受成像质量影响,角速度普遍比较准确,可估计绝对尺度

存在零偏,低精度 IMU 积分位姿发散,高精度价格昂贵

可利用视觉定位信息来估计 IMU 的零偏,减少 IMU 由零偏导,致的发散和累积误差;

视觉 Visual Odometry
• 以图像形式记录数据,频率较低(15 − 60Hz 居多)
• 通过图像特征点或像素推断相机运动

视觉适合计算长时间、慢速的运动。

不产生漂移,直接测量旋转与平移

受图像遮挡,运动物体干扰,单目视觉无法测量尺度,单目纯旋转运动无法估计,快速运动时易丢失

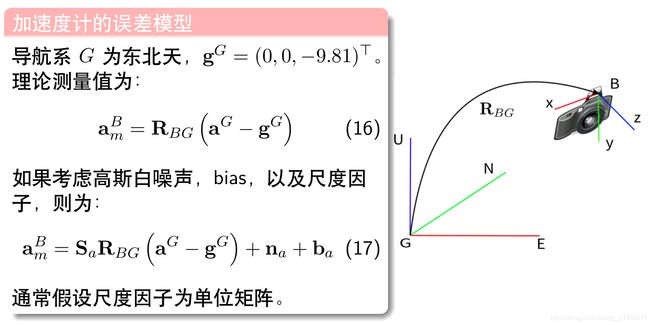
IMU 可以为视觉提供快速运动时的定位

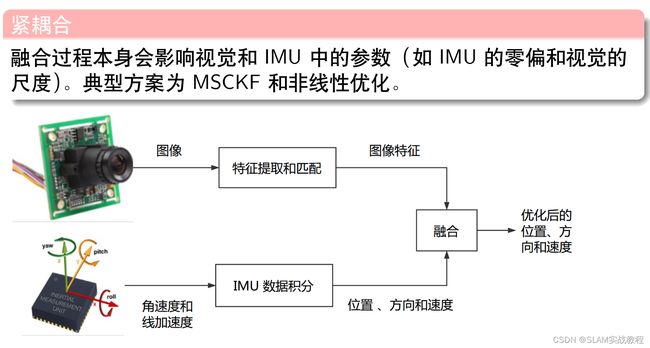
单目视觉或 IMU 不具备估计 Pose 的能力，视觉存在尺度不确定性、IMU 存在零偏导致漂移。
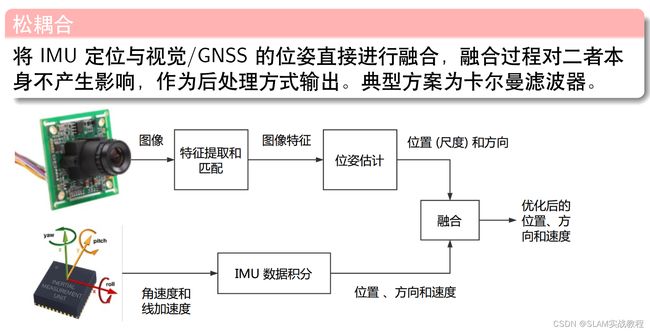
松耦合中：视觉内部 BA 没有 IMU 的信息在整体层面来看不是最优的。
紧耦合中：可以一次性建模所有的运动和测量信息更容易达到最优。

单纯凭(单目)视觉或 IMU 都不具备估计 Pose 的能力:视觉存,在尺度不确定性、IMU 存在零偏导致漂移;
• 松耦合中,视觉内部 BA 没有 IMU 的信息,在整体层面来看不是最优的。
• 紧耦合可以一次性建模所有的运动和测量信息,更容易达到最优。

IMU的加速度

六自由度 IMU 本身由加速度计测量自身的加速度。

IMU的角速度

六自由度 IMU 本身由一个陀螺仪测量自身的角速度。

IMU的零偏(Bias)

https://www.zhihu.com/question/352293998

在陀螺静止时仍会以规定时间内测得的输出量平均值等效输入角速率单位为°/h，°/s。
理想状态下该数值应为地球自转角速度的分量。
在角速度输入为零时陀螺仪的输出是一条复合白噪声信号缓慢变化的曲线，曲线的平均值就是零偏值。

IMU的高斯白噪声

https://www.cnblogs.com/wt869054461/p/7169072.html

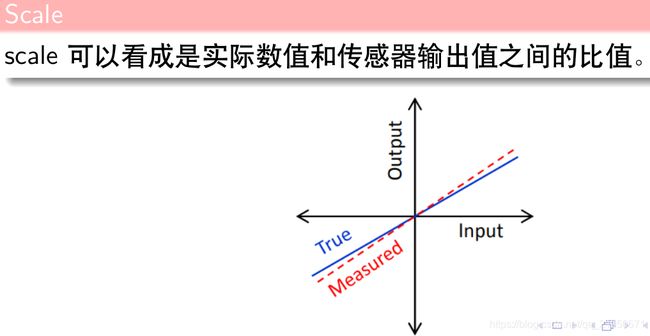
IMU的Scale

VIO 中的 IMU 模型

ORB_SLAM3相机和IMU位置姿态描述

如 I 到 W 系的变换矩阵为:T W I,右乘一个 I 系下(齐次)坐标,将得到该点 W 系下坐标

质量块是我们测量IMU的一部分，是真执行计算的部分，二者分别处于不同的坐标系。

从零手写VIO|第二节——imu.cpp代码解析

用欧拉角表示body坐标系到惯性系的旋转,下方公式表示的是用欧拉角表示从惯性系到body系的转换：

// euler2Rotation:   body frame to interitail frame
Eigen::Matrix3d euler2Rotation( Eigen::Vector3d  eulerAngles)
{
    double roll = eulerAngles(0);
    double pitch = eulerAngles(1);
    double yaw = eulerAngles(2);

    double cr = cos(roll); double sr = sin(roll);
    double cp = cos(pitch); double sp = sin(pitch);
    double cy = cos(yaw); double sy = sin(yaw);

    Eigen::Matrix3d RIb;
    RIb<< cy*cp ,   cy*sp*sr - sy*cr,   sy*sr + cy* cr*sp,
            sy*cp,    cy *cr + sy*sr*sp,  sp*sy*cr - cy*sr,
            -sp,         cp*sr,           cp*cr;
    return RIb;
}

惯性系下的欧拉角速度转换到body坐标系

Eigen::Matrix3d eulerRates2bodyRates(Eigen::Vector3d eulerAngles)
{
    double roll = eulerAngles(0);
    double pitch = eulerAngles(1);

    double cr = cos(roll); double sr = sin(roll);
    double cp = cos(pitch); double sp = sin(pitch);

    Eigen::Matrix3d R;
    R<<  1,   0,    -sp,
            0,   cr,   sr*cp,
            0,   -sr,  cr*cp;

    return R;
}

运动模型的离散积分-欧拉法

运动学模型模型线性化-离散化
https://zhuanlan.zhihu.com/p/156822207

运动模型的离散积分－中值法

B-Spline 产生 IMU数据

B样条曲线（B-spline Curves）
Bezier曲线有以下几个不足点，所以导致出现了B-spline算法：
一旦确定特征多边形，就确定了曲线的阶次
Bezier曲线拼接复杂（需要满足几何连续性，参数连续性等）
Bezier曲线不能作局部修改（只能整体修改）
B-spline算法是整条曲线用一段一段的曲线连接而成，采用分段连续多段式生成
[从零手写VIO|第二节]从已有轨迹生成imu数据推导
从零手写VIO|第二节——imu.cpp代码解析

imusim代码实战教程

imu和cam数据仿真，用于vio算法测试。

创建工作空间
mkdir -p ~/catkin_ws/src
cd ~/catkin_ws/src
catkin_init_workspace
编译工作空间
cd ~/catkin_ws/
catkin_make
当前终端生效的工作空间环境变量配置方法
source  ~/catkin_ws/devel/setup.bash
然后把代码放到src目录下面，再次编译

中值积分和欧拉积分

坐标系

• Body frame: imu坐标系
• Cam frame: 相机坐标系
• World frame: imu坐标系的第一帧位置
• Navigation frame: NED（北东地）or ENU（东北天），本代码采用的是ENU，重力向量在该坐标系下为$(0,0,-9.81)$

目前，imu的z轴向上，xy平面内做椭圆运动，z轴做正弦运动，x轴沿着圆周向外。

外参数Tbc将相机坐标旋转，使得相机朝向特征点。

代码结构

main/gener_alldata.cpp : 用于生成imu数据，相机轨迹，特征点像素坐标，特征点的3d坐标

src/paramc.h：imu噪声参数，imu频率，相机内参数等等

src/camera_model.cpp：相机模型，调用的svo，目前代码里这个文件删掉了

python_tool/：文件夹里为可视化工具，draw_points.py就是动态绘制相机轨迹和观测到的特征点。如果是ubuntu不需额外安装，windows需要安装python matplot等依赖项

数据存储的格式

特征点

x，y，z，1，u，v

每个特征出现在文件里的顺序，就是他们独立的id，可用来检索特征匹配

imu data

timestamp (1)，imu quaternion(4)，imu position(3)，imu gyro(3)，imu acc(3)

cam data

timestamp (1)，cam quaternion(4)，cam position(3)，imu gyro(3)，imu acc(3)

注意，由于imu和cam的存储采用的是同一个函数，所以cam也会存储一些gyro,acc这些数据，但是没用，是多余存储的。

void CreatePointsLines(Points& points, Lines& lines)

using Point = Eigen::Vector4d;

C++11使用using定义别名（替代typedef）

using Points = std::vector >;
EIGEN_MAKE_ALIGNED_OPERATOR_NEW

从Eigen向量化谈内存对齐

C++,vector模板类的问题？ std::vector points；

using Line = std::pair;

STL pair的使用

using Lines = std::vector >;

std::vector使用总结

Eigen::Vector4d pt1( x, y, z, 1 );
lines.emplace_back(pt0, pt1);

生成两个Eigen::Vector4d的点，两个点连成一条线。

emplace_back()和push_back()的区别

emplace_back() 和 push_back() 的区别，就在于底层实现的机制不同。push_back() 向容器尾部添加元素时，首先会创建这个元素，然后再将这个元素拷贝或者移动到容器中（如果是拷贝的话，事后会自行销毁先前创建的这个元素）；而 emplace_back() 在实现时，则是直接在容器尾部创建这个元素，省去了拷贝或移动元素的过程。

C++ STL vector添加元素（push_back()和emplace_back()）详解

Eigen::Quaterniond

三维空间的旋转可以用欧拉角，旋转向量，旋转矩阵，四元数来表示。
欧拉角表示法，我们可以用绕某个轴旋转来表示。
旋转向量就是用一个旋转轴和一个旋转角来表示旋转。
旋转矩阵用一个矩阵来表示空间中的旋转变换关系。
四元数用４个变量来表示旋转增加一个维度，避免万向锁。

Eigen库中各种形式的表示如下
Eigen::AngleAxisd //旋转向量（3*1）
Eigen::Matrix3d //旋转矩阵（3*3）
Eigen::Quaterniond //四元数（4*1）
Eigen::Vector3d //平移向量或欧拉角（3*1）
Eigen::Isometry3d //欧式变换矩阵（4*4）
Eigen::Affine3d      //仿射变换矩阵（4*4）
Eigen::Projective3d  //射影变换矩阵（4*4）
Eigen::Quaterniond q1(w, x, y, z);// 第一种方式,实部是前面的w
Eigen::Quaterniond q2(Vector4d(x, y, z, w));// 第二种方式,实部是后面的w
Eigen::Quaterniond q2(Matrix3d(R));// 第三种方式由旋旋转矩阵构造四元数
Eigen::Quaterniond Qwb;
Qwb.setIdentity();// 表示单位旋转的四元数
Eigen::Quaterniond.coeffs().transpose()
coeffs的顺序是(x,y,z,w) w为实部，前三者为虚部，输出四元数的每一个值。
从零开始手写vio作业-ch1-编程实现旋转的更新(分别用旋转矩阵和四元数实现)
https://blog.csdn.net/joun772/article/details/110133708

Eigen::MatrixXd和VectorXd的用法注意

//方式一：用matrix()
//方式二：用toRotationMatrix()
Eigen::Quaterniond.toRotationMatrix()

将四元数转换为旋转矩阵

时间戳

double dt_tmp = 0.005;
for (double i = 0; i < 20.; i += dt_tmp) {

浅显理解激光雷达的时间同步。

《The swirlds hashgraph consensus algorithm: Fair, fast, byzantine fault tolerance》Hashgraph论文的学习

采用一致的时间戳(当前时间的一个数字序列)，每一个区块（实际上是事件，下文会谈到）以及区块里的每一笔交易都有顺序

无论是相机还是IMU如果同时启动，那么在这个时间就会产生两个数据一个是图像一个是IMU输出的加速度和角速度，假设每一个数据没有时间戳去标记的化，那么再次读取的时候我们怎么确定先后顺序呢？也没办法找到图片输出的那一时刻IMU的数据，所以在去中心化系统中唯一的标识就是时间戳。例如git每一个提交的版本的就是一个时间戳，只不过形式是哈希值，当然我们也可以自己定义规则去生成数字序列。

mkdir("keyframe", 0777);
// 头文件：sys/types.h, sys/stat.h
// 函数：int mkdir(const char *pathname, mode_t mode)

函数：int rmdir(const char *_Path)
头文件：sys/types.h, sys/stat.h
功能：删除文件夹，成功返回0，否则-1。

功能：创建文件夹，返回0为创建成功，否则返回-1。

Linux中创建时会有权限要求，该权限参数可以去了解Linux对于文件权限的设置相关内容，例如：0777表示对文件具有完全的权限。

构造函数

class Param{
public:
    Param();

构造函数（Constructor）名字和类名相同，没有返回值。

如果没有构造函数要通过成员函数 setname()、setage()、setscore() 分别为成员变量 name、age、score 赋值，这样做虽然有效，但显得有点麻烦。

构造函数Student(char *, int, float)，它的作用是给三个 private 属性的成员变量赋值。要想调用该构造函数，就得在创建对象的同时传递实参，并且实参由( )包围，和普通的函数调用非常类似。

不管是构造函数还是普通函数都是定义的时候是形式参数，传递的是实际参数，

构造函数和析构函数的由来

类的数据成员不能在类的声明时候初始化,为了解决这个问题? 使用构造函数处理对对象的初始化。构造函数是一种特殊的成员函数,与其他函数不同,不需要用户调用它,而是创建对象的时候自动调用。析构函数是对象不再使用的时候,需要清理资源的时候调用。

构造函数和析构函数的基本语法

构造函数

• C++中的类需要定义与类名相同的特殊成员函数时,这种与类名相同的成员函数叫做构造函数;
• 构造函数可以在定义的时候有参数;
• 构造函数没有任何返回类型。
• 构造函数的调用: 一般情况下,C++编译器会自动的调用构造函数。特殊情况下,需要手工的调用构造函数。

析构函数

• C++中的类可以定义一个特殊的成员函数清理对象,这个特殊的函数是析构函数;

• 析构函数没有参数和没有任何返回类型;

• 析构函数在对象销毁的时候自动调用;

• 析构函数调用机制: C++编译器自动调用。

  C++类成员的访问权限以及类的封装

  C++构造函数详解

形式参数和实际参数

形参（形式参数）
在函数定义中出现的参数可以看做是一个占位符，它没有数据，只能等到函数被调用时接收传递进来的数据，所以称为形式参数，简称形参。

这里按自己的理解为什么说形参看作一个占位符，后文还说到在调用之前并没有给他分配内存，看上去这两段是有些矛盾的，其实机器在时间上的运行顺序这么说没毛病；

本人理解是在程序编译过程中，程序计数器不断加以程序顺序执行，执行到调用函数位置时，会将之前的数据压栈就像中断一样，调用前要传递实参值对应的内存位置并没有开辟，所以可以说形参再调用前不占内存；

但是这里没有开辟不是说实参会传到随机的位置，这是不会发生的，程序在编译好之后，每执行一条指令，数据都会有个确切的内存位置对应（这是在编译器编译的时候就已经确定好的），所以这么说来，形参确实是一个占位符（占有一个内存地址的位置）；

只是调用前别的参数也可以占用这个位置，但编译器编译的时候肯定不会让一个全局变量的内存地址和分配给形参的内存地址是同一个地址，原因大家应该通过上面的解释也明白编译器在编译时不会让两个没有关联的变量，同时服务于一个地址这样会造成数据的混乱。

就像两个服务员负责同一桌客人时，当客人需要一瓶饮料时，两个服务员分别在不同时刻听到，可能就会造成给客人拿两瓶情况。

实参（实际参数）
函数被调用时给出的参数包含了实实在在的数据，会被函数内部的代码使用，所以称为实际参数，简称实参。

形参和实参的功能是传递数据，发生函数调用时，实参的值会传递给形参。

形参和实参的区别和联系

1. 形参变量只有在函数被调用时才会分配内存，调用结束后，立刻释放内存，所以形参变量只有在函数内部有效，不能在函数外部使用。

2. 实参可以是常量、变量、表达式、函数等，无论实参是何种类型的数据，在进行函数调用时，它们都必须有确定的值，以便把这些值传送给形参，所以应该提前用赋值、输入等办法使实参获得确定值。

3. 实参和形参在数量上、类型上、顺序上必须严格一致，否则会发生“类型不匹配”的错误。当然，如果能够进行自动类型转换，或者进行了强制类型转换，那么实参类型也可以不同于形参类型。

4. 函数调用中发生的数据传递是单向的，只能把实参的值传递给形参，而不能把形参的值反向地传递给实参；换句话说，一旦完成数据的传递，实参和形参就再也没有瓜葛了，所以，在函数调用过程中，形参的值发生改变并不会影响实参。

5. 形参和实参虽然可以同名，但它们之间是相互独立的，互不影响，因为实参在函数外部有效，而形参在函数内部有效。

源地址：https://www.cnblogs.com/zhj868/p/14180848.html

MotionData IMU::MotionModel(double t)

椭圆函数

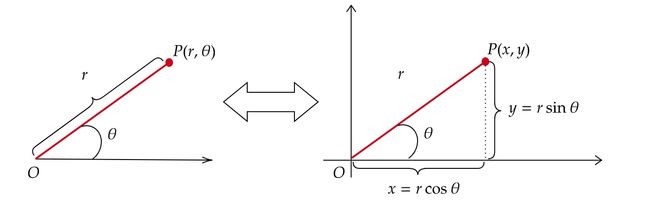
• 圆和椭圆的参数方程是函数. x=acosθ ， y=bsinθ

一.圆锥曲线的参数方程：

​ 圆锥曲线的参数方程与三角换元思想联系紧密。

​ 譬如x2/4 +y2/3=1，把左边两项看成同角正余弦平方之和，列出x2/4=（cosa）2、y2/3=（sina）2

​ 再反解出x与y，此时不需考虑正负号，因为一个角cos与sin可以取遍【-1，1】

​ 最后用大括号将解出的x与y括起来，记得用小括号标注a（你用的那个角）为参数。

​ 双曲线同理。个人推荐题主掌握三角函数的相关思想，这对求取值范围、最值等问题十分有帮助！

​ 二.圆锥曲线的极坐标方程：

​ 用极坐标的定义直接变形。

​ 在以x轴非负半轴为极轴的极坐标系中，所有点都满足x=pcosa、y=psina。

​ 故将上面两式直接带入圆锥曲线方程，即得到了圆锥曲线的极坐标方程。

关于极坐标

极坐标就是：用角度和长度描述位置的坐标系

// param
    float ellipse_x = 15;　// 椭圆短轴
    float ellipse_y = 20;　// 椭圆长轴
    float z = 1;           // z轴做sin运动
    float K1 = 10;          // z轴的正弦频率是x，y的k1倍
    float K = M_PI/ 10;    // 20 * K = 2pi 由于我们采取的是时间是20s, 系数K控制yaw正好旋转一圈，运动一周
    // translation
    // twb:  body frame in world frame
    Eigen::Vector3d position( ellipse_x * cos( K * t) + 5, ellipse_y * sin( K * t) + 5,  z * sin( K1 * K * t ) + 5);

对称中心不在原点的椭圆

Eigen::Vector3d position( ellipse_x * cos( K * t) + 5, ellipse_y * sin( K * t) + 5,  z * sin( K1 * K * t ) + 5);

所以这里就是定义一个对称中心不在原点的椭圆，用极坐标表示。

Eigen::Vector3d dp(- K * ellipse_x * sin(K*t),  K * ellipse_y * cos(K*t), z*K1*K * cos(K1 * K * t));  

一阶导数

Eigen::Vector3d ddp( -K2 * ellipse_x * cos(K*t),  -K2 * ellipse_y * sin(K*t), -z*K1*K1*K2 * sin(K1 * K * t));

二阶导数

float K1 = 10;          // z轴的正弦频率是x，y的k1倍

正弦型函数是形如y=Asin(ωx+φ)+k的函数

A称为振幅，ω称为圆频率或角频率，φ称为初相位或初相角。

往复振动一次所需要的时间T=2π/ω，它叫做振动的周期。

单位时间内往复振动的次数f=1/T=ω/2π，它叫做振动的频率。

Eigen::Vector3d eulerAngles(k_roll * cos(t) , k_pitch * sin(t) , K*t );   // roll ~ [-0.2, 0.2], pitch ~ [-0.3, 0.3], yaw ~ [0,2pi]

https://blog.csdn.net/qq_21950671/article/details/100080945

euler2Rotation

欧拉角和旋转矩阵的转换

Eigen::Vector3d euler_angles = R.eulerAngles(2, 1, 0)：旋转矩阵R用欧拉角euler_angles表示。 
//旋转向量使用AngleAxis，运算可以当做矩阵沿着Z轴旋转45°
AngleAxisd rotation_vector(M_PI / 4, Vector3d(0,0,1));   


Eigen::Matrix3d euler2Rotation( Eigen::Vector3d  eulerAngles)
{
    double roll = eulerAngles(0);
    double pitch = eulerAngles(1);
    double yaw = eulerAngles(2);
 
    double cr = cos(roll); double sr = sin(roll);
    double cp = cos(pitch); double sp = sin(pitch);
    double cy = cos(yaw); double sy = sin(yaw);
 
    Eigen::Matrix3d RIb;
    RIb<< cy*cp ,   cy*sp*sr - sy*cr,   sy*sr + cy* cr*sp,
            sy*cp,    cy *cr + sy*sr*sp,  sp*sy*cr - cy*sr,
            -sp,         cp*sr,           cp*cr;
    return RIb;

欧拉角转旋转矩阵

Mat eulerAnglesToRotationMatrix(Vec3f &theta)
{
    // Calculate rotation about x axis
    Mat R_x = (Mat_(3,3) <<
        1,       0,              0,
        0,       cos(theta[0]),   -sin(theta[0]),
        0,       sin(theta[0]),   cos(theta[0])
    );
    // Calculate rotation about y axis
    Mat R_y = (Mat_(3,3) <<
        cos(theta[1]),    0,      sin(theta[1]),
        0,               1,      0,
        -sin(theta[1]),   0,      cos(theta[1])
    );
    // Calculate rotation about z axis
    Mat R_z = (Mat_(3,3) <<
        cos(theta[2]),    -sin(theta[2]),      0,
        sin(theta[2]),    cos(theta[2]),       0,
        0,               0,                  1
    );
    // Combined rotation matrix
    Mat R = R_z * R_y * R_x;
    return R;
}
Vec3f rotationMatrixToEulerAngles(Mat &R)
{
    float sy = sqrt(R.at(0,0) * R.at(0,0) +  R.at(1,0) * R.at(1,0) );
    bool singular = sy < 1e-6; // If
    float x, y, z;
    if (!singular)
    {
        x = atan2(R.at(2,1) , R.at(2,2));
        y = atan2(-R.at(2,0), sy);
        z = atan2(R.at(1,0), R.at(0,0));
    }
    else
    {
        x = atan2(-R.at(1,2), R.at(1,1));
        y = atan2(-R.at(2,0), sy);
        z = 0;
    }
    #if 1
    x = x*180.0f/3.141592653589793f;
    y = y*180.0f/3.141592653589793f;
    z = z*180.0f/3.141592653589793f;
    #endif
    return Vec3f(x, y, z);
}

旋转矩阵到欧拉角

//由旋转矩阵计算欧拉角
        private double[] rotationMatrixToEulerAngles(double[] M)
        {
            double R00 = M[0], R01 = M[1], R02 = M[2];
            double R10 = M[4], R11 = M[5], R12 = M[6];
            double R20 = M[8], R21 = M[9], R22 = M[10];
 
            double sy = Math.Sqrt(R00 * R00 + R10 * R10);
 
            bool singular = sy < 1e-6; // If
 
            double x, y, z;
            if (!singular)
            {
                x = Math.Atan2(R21, R22);
                y = Math.Atan2(-R20, sy);
                z = Math.Atan2(R10, R00);
            }
            else
            {
                x = Math.Atan2(-R12, R11);
                y = Math.Atan2(-R20, sy);
                z = 0;
            }
            x = x * 180.0 / Math.PI;
            y = y * 180.0 / Math.PI;
            z = z * 180.0 / Math.PI;
            double[] angle = new double[3] { x, y, z };
            return angle;
        }

从两帧IMU数据中获得当前位姿的预测思路非常简单，

无非是求出当前时刻与下一时刻+1加速度的均值， 把它作为Δ时间内的平均加速度，有了这个平均加速度及当前时刻的初始速度和初始位置，就可以近似的求出+1时刻的速度和位置。

求出当前时刻与下一时刻+1角速度的均值， 把它作为Δ时间内的平均角速度，有了这个平均角速度及当前时刻的姿态，就可以近似的求出+1时刻的姿态。

但是由于IMU的数据存在着坐标系、bias和重力加速度的问题需要额外的一些处理。
首先对于加速度，因为imu的加速度数据是在Body坐标系下表示的，所以要利用对应时刻的姿态将其转换到世界坐标系下，转换之前要减去bias，转化之后要减去重力加速度（世界坐标系下的重力加速度恒等于9.8）

加速度计（accelerometer）

陀螺仪（gyroscope，也称作 gyro）

加速度传感器的单位是g，陀螺仪的单位是 度/秒

加计和陀螺仪都能计算出姿态，但为何要对它们融合呢，是因为加速度计对振动之类的扰动很敏感，但长期数据计算出的姿态可信，而陀螺仪虽然对振动这些不敏感，但长期使用陀螺仪会出现漂移，因此我们要进行互补，短期相信陀螺，长期相信加计。不过，其实加计无法对航向角进行修正，修正航向角需要磁力计，也就是下次要总结的9轴数据融合。

在融合之前先要对传感器原始数据进行一些处理。理想情况下，加速度计水平放置时，XY轴应该是0输出的，仅Z轴输出1个G，因此，我们需要对加速度计进行XY轴的零点校准（注意Z轴可不能一起校准去了~）；同样的，陀螺仪在水平静止放置时各轴输出应为0，因此需对陀螺仪进行三轴的校准。方法就是把机体标准水平静止放置时采集它个一两百次数据求个平均作为校准值保存起来喽，然后工作状态下各轴输出的数据就是采集来的数据减去校准值喽。仅此还不够，陀螺仪不进行滤波还可以接受，但加速度计噪声比较大，所以至少也得来个滑动窗口滤波，我用了20深度的滑动窗口，数据还是有很大波动，不过最后计算出的姿态角只有0.3度左右的抖动（我看大家一般都是建议8深度就够了，所以单滑动窗口滤波效果是没法做到更好了，可以考虑加个卡尔曼滤波？还没研究，不过这样处理器运算量就上去了）。（11.28补充：后面改对加计使用8深度滑动滤波，陀螺仪进行16阶凯撒窗滤波后只有0.1不到的波动，不过凯撒滤波参数的整定还不会，用的别人整定的一组参数，近期继续研究）。滤波效果如图：

加速度是速度对时间的一阶求导。

位移对时间的一阶导数，就是位移随时间的变化率，其物理意义就是速度；
位移对时间的二阶导数，就是位移随时间变化率随时间的变化率，也就是速度随时间的变化率，其物理意义就是加速度。

加速度是由作用在物体上的外力和物体的质量决定的。

v = ds/dt，速度是单位时间里位移的变化，也就是说速度 v 是位移 s 对时间 t 的一阶导数。
a = dv/dt，意思就是加速度是单位时间里速度的变化，也就是说，加速度 a 是速度 v 对时间 t 的一阶导数，是位移 s 对时间 t 的二阶导数。

IMU 姿态估计的第一步是将陀螺仪（gyroscope）测量的角速度积分成陀螺仪的姿态。

我们将介绍三种形式的积分方法：分别使用旋转矩阵、四元数和欧拉角。在这些方法中，我们不考虑地球自身的旋转和地球的曲率，因此只限于小范围内的 IMU 的应用。在开始之前，我们先做一个约定：在本文中所有的角速度 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wb3JGbxi-1609298398225)(https://www.zhihu.com/equation?tex=%5Cbm%7B%5Comega%7D)] 指旋转坐标系（IMU坐标系）相对于固定坐标系（地球坐标系）的角速度，并且 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-bP8BOIP7-1609298398226)(https://www.zhihu.com/equation?tex=%5Cbm%7B%5Comega%7D)] 的坐标表示在旋转坐标系中。

IMU姿态估计

尽管刚体的姿态有很多种不同的表示方法，它们的积分方法也不相同，但这其中有一些共通的地方，在这里作一些简要但不严格的介绍。刚体旋转群 SO(3) 是一个李群，所谓李群是指同时具有光滑流形和群的结构的空间，同时群内的运算也是光滑的。李群的定义需要花很长篇幅解释清楚，也不重要，在这篇文章中我们需要知道的是 SO(3) 上的每一个旋转，都有一个切空间。这个切空间是一个线性空间，它的维数与 SO(3) 相同，即具有三个自由度。在李群的语言中，切空间也叫做李代数（Lie Algebra）。切空间的直观理解是：切空间内的每一个向量代表了一个速度，并且这个速度可以通过李群的性质积分成一个位移，而这个积分就是李群的指数映射（exponential map）。可以证明指数映射在局部是一一对应的，也就是每个速度都对应了唯一一个位移。

4.1 IMU误差模型

陀螺仪和加速度计的系统误差一般包含以下几种：开机后恒定的零偏误差（bias），比例因子误差（scale factor），不重合及非正交误差（misalignment and non-orthogonality），非线性误差（non-linearity），温度误差（thermal noise）。其中陀螺仪还包含加速度的变化引起的误差（g-dependent noise）[1]。因此包含系统误差的角速度可以写为以下的表达式：

2. 陀螺仪和加速度计的随机误差-随机行走

使用ROS版本的代码得到静态仿真数据 .bag格式 使用Allan方差标定IMU参数

1. 回放数据包运行imu_utils
2. 标定结果后处理
3. 标定结果与设定参数对比
   
   使用imu_utils的结果处理
   
   使用imu_utils的结果后处理
   

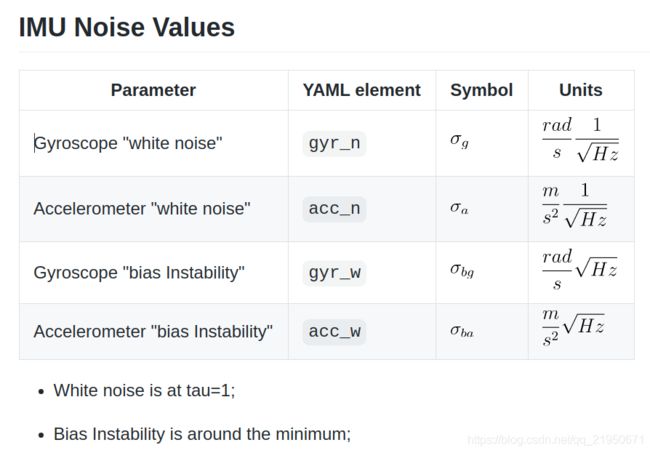
白噪声 white noise
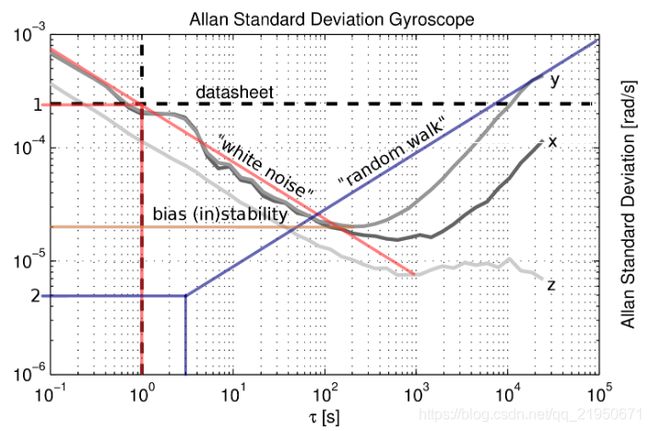
双对数图上拟合的斜率为-0.5的直线与τ = 1s的交点纵坐标

零偏不稳定性 bias instability
一般取双对数图上斜率为零且最小点的纵坐标

速率随机游走 rate random walk
双对数图上拟合的斜率为0.5的直线与τ = 3s的交点纵坐标

Imu_utils 输出的是白噪声和零偏不稳定性,我们需要标定的参数是白噪声和速率随机游走,所以得不到需要的
所有参数

参考资料

多传感器融合定位（3-惯性导航原理及误差分析）8-惯性导航解算验证

在现实中 高精度惯导中用等效旋转矢量，低精度惯导中，用角增量；一般中低精度的导航里面，提高的比例都在10%以内，没有太高；实际系统中可以做个实验对比一下，看能提高多少，来决定要不要使用等效旋转矢量的方法解算

我们先来回顾一下姿态更新的框架图
两种姿态解算方法：
1.使用theta t 时间内角增量做积分中值处理
2.使用角增量求解等效旋转矢量的方法

注：表征姿态变化，一般使用四元数较为方便

旋转矩阵（Rotation Matrix）的推导及其应用

imu_utils

A ROS package tool to analyze the IMU performance. C++ version of Allan Variance Tool. The figures are drawn by Matlab, in scripts.

Actually, just analyze the Allan Variance for the IMU data. Collect the data while the IMU is Stationary, with a two hours duration.

https://pan.baidu.com/disk/home?#/all?vmode=list&path=%2Fimu_dataset

下载仿真代码
cd  ~/catkin_ws/src git clone https://github.com/HeYijia/vio_data_simulation/tree/ros_version
bag.open("./imu.bag", rosbag::bagmode::Write);// 修改vio_data_simulation/src/gener_alldata.cpp中imu.bag的存储路径为：
cd ~/catkin_ws
catkin_make
source  ./devel/setup.bash
roscore
cd ~/catkin_ws/devel/lib/vio_data_simulation// 生成包imu.bag包即是仿真得到的IMU数据，后续使用这个包里的数据生成Allan方差。
rosrun vio_data_simulation vio_data_simulation_node
    

https://blog.csdn.net/YunLaowang/article/details/95608107

VIO标定IMU随机误差：Allan方差法
陀螺 Allan 方差分析

在IMU选型时，需要重点关注陀螺的随机游走和零偏稳定性参数，这些是影响姿态精度的主要参数。

一般，芯片手册上给定的参数比较理想。需要在拿到硬件后，进行误差分析，多次测试看其性能。

Allan方差法是一种时域分析技术，对实际静态条件下采集的惯性器件数据进行分析得到双对数曲线图，如图1, 根据不同拟合直线的斜率可以辨识不同的误差系数。

Allan方差分析的使用要点

\1. Allan方差分析主要用于分析陀螺量化噪声、角度随机游走噪声（角速率白噪声）、零偏不稳定性、角速率随机游走（角加速度白噪声）和速率斜坡（角速率常值趋势项），等五种典型误差。有些文献也提到可用于分析周期项和一阶马尔可夫误差，但这不是Allan方差分析的强项，周期项更适合用功率谱分析，马尔可夫更适合于用相关分析（时间序列分析），不要试图以己之短攻人所长！

\2. Allan方差分析的是静态误差，陀螺必须在静基座下进行采集数据，否则要是动基座下采集的陀螺数据，分析的结果到底是陀螺误差呢还是基座运动特性？！

\3. Allan方差计算中采用了“差分”计算操作，因此Allan方差无法分析获得陀螺随机常值漂移参数。若是将几个陀螺的Allan方差曲线同时绘制在同一个双对数图上，曲线在左下角的对应的陀螺性能一般较好些，而右上角的差些。如下图从下到上分别为激光陀螺、光纤陀螺和MEMS陀螺，其中激光陀螺性能最好。如果是同一类型的陀螺，也是左下角的曲线性能稍好些。

\4. Allan方差可用于分析五种典型误差，但是某个陀螺中并不一定五种误差都有同时表现出来，不画Allan方差图/不肉眼看图，而盲目的采用最小二乘回归方法强行地就想求解五个系数的人是典型的教条主义者，往往得不到好的结果。比如如下Allan方差图中y曲线所示（摘自https://github.com/ethz-asl/kalibr/wiki/IMU-Noise-Model），采用“三段论”大概读图计算角度随机游走系数、零偏不稳定性和角速率随机游走（或速率斜坡）即可，完全可满足实际应用。过细分析想得出精确系数的人都是有洁癖的。

\5. 如下图红圈中的Allan方差并不是什么马尔可夫过程噪声的，往往是由于陀螺经过低通滤波器后造成的，这时Allan方差反映的是滤波器的特性，而不是实际陀螺的特性。因此要得到陀螺的本质特性，应该对陀螺作高频采样，并且不能对原始数据做任何处理，直接用Allan方差分析才行。

\6. Allan方差分析的一个用途是分析陀螺的性能或对比不同陀螺的性能，如前3所述，相比于其它分析法Allan法还是很好用的，比较全面。另一个用途是获得噪声参数，用于组合导航的Kalman滤波噪声参数设置。不是所有的Allan方差噪声系数都有用，主要有用的是角度随机游走系数（用于设置Q阵）和零偏不稳定性系数（用于设置一阶马氏过程的方差），其实这两个系数量级大小差不多就行了，太精细也没用。毕竟Allan方差分析的只是一个样本，你再采一个样本试试，肯定会有差异的；此外采集的是陀螺的静态性能数据，鬼知道实际动态应用的时候陀螺误差会变化多大，存在数量级差别都很有可能。这里需要的是理论指导下的工程和经验，而不是教条主义。

\7. 老外给MEMS陀螺指标喜欢用Allan方差，也就是Allan方差图的最低点，比如下图stim202，说该陀螺精度是0.5deg/h。其实国内喜欢用10s平滑结果，从图中直接读10s对应的大概是4deg/h。数值“0.5deg/h”表面看着挺振奋的，实际不要被它迷惑，它对应的时间横坐标是3000s多，谁用陀螺也不会静止这么长时间！而且该误差是一次启动稳定性，而不是逐次启动重复性，也许该陀螺逐次重复性有可能几十甚至上百deg/h。使用该陀螺在静态下是不能找北的，不要被“0.5deg/h”迷惑。当然在目前MEMS陀螺世界中，stim202性能还是相对很优秀的。

\8. 如果画出的Allan方差图形不像典型的U型或V型图，极端如下，不要感觉到诧异，也不要再试图用Allan方差去分析它（又是教条主义），没意义！此时Allan分析失效，应试图对原始数据作分析和解释。

\9. Allan方差分析理论可参见《惯性仪器测试与数据分析》第八章，程序可见psins工具箱中的avar函数，用不着太复杂的计算方法。

B样条曲线（B-spline Curves）

是B-样条基曲线（给定区间上的所有样条函数组成一个线性空间。这个线性空间的基函数就叫做B样条基函数）的线性组合。

B-样条是贝兹曲线的一种一般化，B样条不能表示一些基本的曲线，比如圆，所以引入了NURBS,可以进一步推广为非均匀有理B-样条(NURBS)。三者关系可以表示为：

B样条曲线曲面（附代码）

B样条方法具有表示与设计自由型曲线曲面的强大功能，是形状数学描述的主流方法之一，另外B样条方法是目前工业产品几何定义国际标准——有理B样条方法 (NURBS)的基础。B样条方法兼备了Bezier方法的一切优点，包括几何不变性，仿射不变性等等，同时克服了Bezier方法中由于整体表示带来不具有局部性质的缺点（移动一个控制顶点将会影响整个曲线）。B样条曲线方程可表示为

B-样条曲线教程（B-spline Curves Notes）目录

本教程是关于B-样条曲线（B-spline Curves）的教程。B-样条曲线在计算机视觉(computer vision )，计算机图形学（Computer Graphics ），计算机辅助设计（Computer-Aided Design ），计算几何（Computational Geometry ） ，可视化（Visualization）等许多领域有着广泛应用。

B-spline Curves 学习之B样条基函数的定义与性质（2）

IMU姿态、速度、位置解算以及误差方程

【ORB_SLAM2源码解读】坐标变换 Eigen、Sophus、旋转矩阵、轴角、旋转向量、欧拉角、四元数、位姿变换

旋转向量求导数

假设某个旋转运动的旋转轴为单位向量 u，绕该轴旋转的角度为 θ,那么它对应的单位四元数为:

当旋转一段微小时间,即角度趋于 0 时,容易有:

其中 δθ 的方向表示旋转轴,模长表示旋转角度。角速度:

四元数对时间求导数

应用李代数对旋转矩阵求导数

使用旋转矩阵 R 时,角速度为 ω,那么 R 相对于时间的导数可写作:

该式被称为泊松公式(Possion’s equation),其中${}^{\wedge }$为反对称矩阵算子:${\omega }_{\times }$ 或者 $[\omega {]}^{\times }$ ,表达含义相同。

so(3) 导数

在优化带有旋转的函数时,通常计算一个增量 φ ∈ so(3),然后用它更新当前估计值:

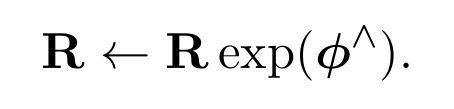
其中 exp 为 so(3) 至 SO(3) 上的指数映射。
习惯为右乘,实际当中左右乘等价,仅为习惯上的差别。
注:(i) 不同的 R 函数,具体的导数形式也不同。(ii) 在程序中,不必区分 R 是以矩阵存储或是以四元数存储,只需按照该式更新即可。

旋转点的左扰动雅可比

旋转点的右扰动雅可比

旋转连乘的雅可比

旋转连乘的雅可比

有关 SE(3)

由于 SE(3) 李代数性质复杂,在 VIO 中,我们通常使用SO(3) + t 的形式表达旋转和平移。对平移部分使用矢量更新而非SE(3) 上的更新。

四元数和李代数更新

可以使用旋转矩阵和四元数存储旋转变量，用计算出来的 ω 对某旋转更新时，有两种不同方式

对于小量 ω = [0.01, 0.02, 0.03] T ,两种方法得到的结果非常接近,实践当中可视为等同。因此后文提到旋转时并不刻意区分旋转本身是 q 还是 R,也不区分其更新方式为上式的哪一种。

使用右乘 so(3) 推导以下导数

位置、速度、姿态解算

目的：利用IMU测量的角速度、加速度，根据上一时刻信息，推算出当前时刻的姿态、速度、位置。
方法：由姿态、速度、位置的微分方程，推导出它们的解，并转变成离散时间下的近似形式，从而可以在离散时间采样下，完成姿态、速度、位置信息求解。
优点：IMU不受外界信号干扰，可以得到稳定、平滑的导航结果。
缺点：误差随时间累计，一般时间越长，累计误差越大。因此需要融合，而姿态、速度、位置解算及其误差分析，是融合的基础。

姿态更新

基于旋转矩阵求姿态

基于旋转矩阵的姿态更新

基于四元数的姿态更新

速度更新

位置更新

加速度计的误差模型

陀螺仪的误差模型

姿态误差方程

速度误差方程

位置误差方程

bias误差方程

坐标系