attention mechanism in computer vision(1)——channel attention

attention mechanism in computer vision(1)——channel attention

---

一、attention的一般模式：

Attention = f(g(x), x)，g(x)代表了识别出重要区域的过程，f(g(x), x）代表了从识别出的重要区域获取信息的过程，几乎所有现有的注意机制都可以写入上述公式中：

二、Channel attention

深度神经网络中，不同特征图中的不同信道通常代表不同的对象。通道注意自适应地重新校准每个通道的权重，可以看作是一个对象选择过程，从而决定需要注意什么。 第一个提出这个概念的并使用上的模型是SENet，随后的工作还有GSop-Net,SRM,GCT,ECANet,FcaNet,EncNet,Bilinear attention

三、总结

把总结放在这里是方便直接查看结果，后面细节之类的太多，为了方便直接看各种模型的结构、优略、作者信息什么的：
模型的结构：

提供了net的出版信息，常用于的任务，最重要的g(X)，f(g(X),X)结构，soft attention还是hard attention：

四、细节解释：

稍微解释部分，最多只是让我自己看懂，如果觉得不太详细，自己去看论文或看看其它博客文章吧

1、SENet

senet的全称为Squeeze-and-Excitation Networks，压缩-激活网络
Sequeeze：对进行global average pooling，得到
大小的特征图，这个特征图可以理解为具有全局感受野。
Excitation ：使用一个全连接神经网络，对Sequeeze之后的结果做一个非线性变换。
特征重标定：使用Excitation 得到的结果作为权重，乘到输入特征上。
效果：分类网络现在一般都是成一个block一个block,se模块就可以加到一个block结束的位置，进行一个信息refine。这里用了一些STOA的分类模型如：resnet50,resnext50，bn-inception等网络。通过添加SE模块，能使模型提升0.5-1.5%,效果还可以，增加的计算量也可以忽略不计。在轻量级网络MobileNet,ShuffleNet上也进行了实验，可以提升的点更多一点大概在1.5-2%。但是SE使用的是GAP，在squeeze model中，全局平均池太简单，无法捕获复杂的全局信息。在excitation model中，全连接层增加了模型的复杂性。

从attention的角度描述：SE Block被分成两个部分，即squeeze module和excitation model,通过全局平均池化，在squeeze model中收集全局空间信息。excitation model通过使用全连接层和非线性层(ReLU和sigmoid)来捕获信道级关系并输出注意向量。然后，通过乘以注意向量中相应的元素，对输入特征的每个通道进行缩放,放在attention的通用模式中的公式就是:

2、GSoP-Net

SE块仅通过使用全局平均池（即一阶统计信息）来捕获全局信息，这限制了其建模能力，特别是捕获高阶统计信息的能力,而GSoP-Net主要在squeeze model使用了全局二阶池(GSoP)块，在收集全局信息的同时建模高阶统计数据。
操作步骤：首先通过一个1X1卷积层降低层数，然后计算不同信道的协方差矩阵，得到它们的相关性。得到的协方差矩阵具有明确的物理意义，即其第i行表示通道i与所有通道的统计相关性。由于所涉及的二次操作改变了数据的顺序，为了保证固有的结构信息，接下来，对协方差矩阵进行行级归一化，然后应用一个全连接层和一个sigmoid函数得到一个c维注意向量。
通过使用二阶池化，GSoP块提高了通过SE块收集全局信息的能力。然而，这是以额外的计算为代价的。因此，通常在几个残差块之后添加单个GSoP块。

从attention角度描述：

3、SRM

SRM将风格转移与注意机制结合起来。它的主要贡献是风格池，它利用输入特征的均值和标准差来提高其捕获全局信息的能力，它还采用了一个轻量级的通道全连接(CFC)层，以代替原来的全连接层，以减少计算需求，它由两个主要组件组成：Style Pooling 和 Style Integration。Style Pooling 运算符通过汇总跨空间维度的特征响应来从每个通道提取风格特征。紧随其后的是 Style Integration 运算符，该运算符通过基于通道的操作利用风格特征来生成特定于示例的风格权重。

Style Pooling：定输入特征图 (N,C,H,W)，通过以下方式计算样式特征(N,C,d) ,一般来说d=2：

风格矢量 用作每个示例 [公式] 和通道 [公式] 的风格信息的总结描述。其他类型的风格特征，例如不同通道之间的相关性也可以包含在样式向量中，但是为了效率和概念上的清晰，这里只专注于按通道统计。

Style Integration：
风格集成运算符将风格特征转换为通道方式的风格权重。风格权重应该被用来建模与各个通道关联的风格的重要性，从而相应地强调或压抑它们。为了实现这一点，我们采用了通道级完全连接（CFC）层，批标准化（BN）层和 Sigmoid 激活函数的简单组合。给定风格表示形式$TϵR^{N\cdot C\cdot 2}$ 作为输入，风格集成运算符使用可学习的参数$WϵR^{C\cdot 2}$ 进行通道编码,这里做的是点积：

可以将此操作视为具有两个输入节点和一个输出的独立于通道的完全连接层，其中偏置项被吸纳到随后的BN层中。然后，我们应用BN来促进训练和将 Sigmoid 函数作为门控机制：

从attention角度：给定一个输入特征图$XϵR^{C.H.W}$，SRM首先使用样式池(SP（·）)收集全局信息，该样式池结合了全局平均池和全局标准偏差池。然后利用通道全连接（CFC（·））层（即每个通道全连接）、批归一化BN和s型函数σ提供注意向量。最后，就像在一个SE块中一样，将输入特征乘以注意向量。总的来说，一个SRM可以写成：

4、GCT

SENet在squeeze model采用了两个全连接层，导致计算复杂度增加，一般只能在几个残差块之后加上一个SE块，而且全连接是一种隐式表达，但是GCT的核心部分归一化没有参数，后面部分门控自适应操作符的参数易于可视化，可以直观地解释GCT的行为。这种少参数的单元容易部署，可以把它看成batch normalization一般的轻量级护理。部署GCT层有三个可能的点，分别是在卷积层之前、归一化层之前和归一化层之后。
如图，输入的feature map 经过 Global Context Embedding，Channel Normalization，Gating Adaptation

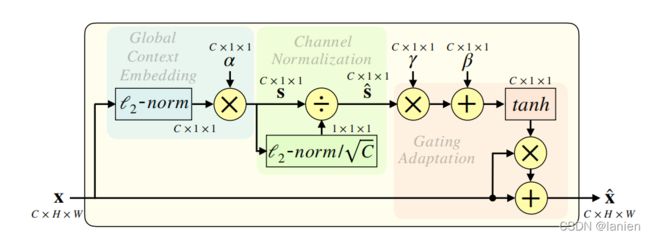
1、Global Context Embedding：不同于前面几个模型，这里先采集全局的信息

汇聚。给定嵌入参数$\alpha =[{\alpha }_1,{\alpha }_2...{\alpha }_c]$ ，该模块定义如上图：
其中， 为极小常识用于避免倒数为0。不同SE，GCT并未使用全局均值池化进行通道上下文信息汇聚。作者认为GAP在某些极限情况下会失效，比如SE位于Instance Normalization之后时GAP的输出将是常数，因为IN会固化通道特征的均值。为避免上述问题，作者提出采用了 范数进行替代，GCT对不同${\iota }_p$ 具有较好的鲁棒性，最佳者是${\iota }_2$。
此外，我们提出采用可训练参数 用于控制不同通道的重要性。特别的当$\alpha$ 近似于0时，通道c将不会被纳入到通道规范化中。也就是说 使得GCT能学习极限情形：单通道起作用。

2、Channel Normalization：
规范化可以通过少量计算资源构建神经元间的竞争关系，类似于LRN，作者采用 ${\iota }_2$进行跨通道特征规范化，即通道规范化，此时定义如下：

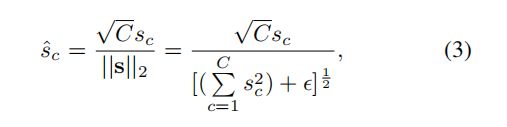
3、Gating Adaptation：在前述基础上添加了门限机制，通过引入门线机制，GCT可以有助于促进神经元的竞争or协同关系。定义如下：

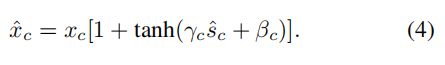
由于通道规范化是无参数操作，作者设计了一组可训练参数$\gamma$ ,$\beta$ 用于控制通道门线。不同于LRN仅促进通道竞争，GCT可以同时促进通道竞争与协同关系。当通道的门限权值为正时，GCT取得了类似LRN的通道竞争关系；当通道的门限权值为负时，GCT取得了通道协同作用。

从attention的角度：

效果：GCT块比SE块的参数更少，而且由于它具有轻量级的特性，因此可以在CNN的每个卷积层之后添加。

5、ECANet

为了避免较高的模型复杂度，SENet减少了通道的数量，但是作者通过实验发现避免降维对于学习通道注意力非常重要，适当的跨信道交互可以在显著降低模型复杂度的同时保持性能。为此提出了一种有效的通道关注(ECA)模块，该模块只增加了少量的参数，却能获得明显的性能增益。
下图为ECA模块，输入的feature map先经过一个GAP,输出一个(1,1,C)的向量，再将这个向量经过一个1D的卷积，核的大小K是可以学习的，最后得到权重向量：

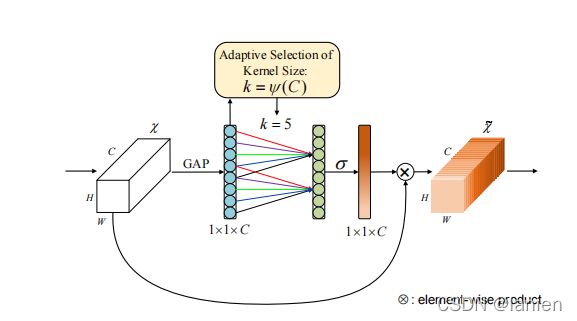
k和C之间存在映射，由于通道维数通常是2的指数倍，所以，这里采用以2为底的指数函数来表示非线性映射关系:

得到（$\gamma$和b是超参数，实验一般分别是2，1，${\left|t\right|}_{odd}$表示最接近t的奇数）：

从attention的角度：ECA块与SE块具有类似的公式，包括用于聚合全局空间信息的squeeze model和用于建模跨信道交互的有效exitation model。不同于SENet的间接的通道交互，ECA块只考虑每个通道与其k个最近邻之间的直接交互，以控制模型的复杂性。

效果：与SENet相比，ECANet具有改进的exitatioon model，并提供了一个高效、有效的模块，可以很容易地集成到各种CNN。

6、FcaNet

Squeeze model的GAP缺乏表征能力，作者证明了全局平均池化是离散余弦变换(DCT)的一种特殊情况，为了增强模型的表征能力，利用这一观察结果，提出了一种新的多光谱通道注意方法（multi-spectral channel attention），下图是FcaNet的结构。

步骤：给定一个输入特征图$XϵR^{C.H.W}$，多光谱通道注意首先将X分成许多部分$X^iϵR^{C^{{}^{\prime }}.H.W}$。然后对每个部分$X^i$应用一个二维DCT,2D的DCT可以使用预处理结果来减少计算量。在处理每个部分后，所有的结果都被连接到一个向量中。然后经过一个全连接，一个sigmoid激活函数。

从attention角度:

该工作基于信息压缩和离散余弦变换，在分类任务上取得了良好的性能。

7、EncNet

这篇文章我没大看懂，可以参考博客https://blog.csdn.net/u011974639/article/details/79806893

8、 Bilinear Attention

以往的注意模型只使用一阶信息，而不考虑高阶统计信息。因此，他们提出了一种新的双线性注意块（双注意），在保留空间信息的同时，捕获每个通道内的局部成对特征交互作用。双注意采用在注意中的注意(AiA)机制来获取二阶统计信息：从内信道注意的输出中计算出外点向信道注意向量。
给定输入特征图X，双注意首先使用bilinear pooling来捕获二阶信息：

其中$\varphi$表示用于降维的embedding function，Utri（·）提取矩阵的上三角元素，Vec（·）是向量化。
接下来将内通道注意机制应用于$\tilde{x}ϵR^{\frac{c^{{}^{\prime }}(c^{{}^{\prime }}+1)}{2}.H.W}$上：

这里的ω和ϕ也是embedding function。
最后，利用输出特征图$\hat{x}$计算最终的空间通道注意权重

效果：
bi_attention利用bilinear pooling对沿每个通道的局部成对特征交互进行建模，同时保持空间信息。由于利用了所提出的AiA，与其他基于注意力的模型相比，该模型更关注高阶统计信息。双注意力可以被纳入任何CNN主干中，以提高其表征能力，同时抑制噪声