题目 全题解 2022年第十三届蓝桥杯省赛 C/C++b组 含解析

题目 全题解 2022年第十三届蓝桥杯省赛 C/C++b组 含解析

---

---

经过简单测试基本正确，测试网站

试题 A: 九进制转十进制

1478
（29^3+29+2=1478）

试题 B: 顺子日期

争议性很强的一个题，主要是012算还是321算
我这里按照012算来写的，14个
（20221012 20221123 20221230 20221231 2022012X(x为0~9)

试题 C: 刷题统计

方法一：二分答案

写了个蛇皮写法

#include
using namespace std;
using ll = long long;
using ull = unsigned long long;
int main() {
	ull a, b, n;
	cin >> a >> b >> n;

	ull ans = 0;

	ull l = 1, r = (7 * n / (a + b)) + 1;
	while (l < r) {
		ull m = ((r - l) >> 1) + l;
		ull cost = 0;
		cost += ((m / 7) * 5 + min<ull>(m % 7, 5)) * a;
		cost += ((m / 7) * 2 + (m % 7 == 6 ? 1 : 0)) * b;
		if (cost >= n) r = m;
		else l = m + 1;
	}
	cout << l;
	return 0;
}

方法二：数学

建议直接计算即可

#include
using namespace std;

int main() {
	int64_t a, b, n;
	cin >> a >> b >> n;
	auto w = n / (a * 5 + b * 2);
	n = n - w * (a * 5 + b * 2);
	w = w * 7;
	for (int i = 0; n > 0; ++i) {
		if (i < 5) n -= a;
		else n -= b;
		++w;
	}
	cout << w;
	return 0;
}

试题 D: 修剪灌木

方法一：脑筋急转弯（划掉）

这个数据范围……含不含1啊，应该不含吧
含1要特判一下 输出1而不是0（但是这个范围……）

#include
using namespace std;
int main() {
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i) {
		cout << (max(n - i - 1, i) * 2) << endl;
	}
	return 0;
}

试题 E: X 进制减法

方法一：数学 + 贪心

用x进制做减法，然后按照最小进制转回10进制就行了，不知道理解的对不对

#include

using namespace std;

using ll = long long;
using ull = unsigned long long;
using pii = pair<int, int>;
using db = double;

static int stream_off = []() {
	std::ios::sync_with_stdio(false);
	cin.tie(NULL);
	return 0;
}();//关闭流同步，注意不要和c式输入同时使用（如快读板子）

int main() {
	ll n;
	cin >> n;
	ll ma, mb;
	cin >> ma;

	vector<ll> a(ma), b(ma), c(ma);
	vector<ll> q(ma, 2);
	for (int i = 0; i < ma; ++i) {
		cin >> a[i];
	}

	cin >> mb;

	for (int i = ma - mb; i < ma; ++i) {
		cin >> b[i];
	}
	
	for (int i = 0; i < ma; ++i) {
		q[i] = max({ q[i], a[i] + 1, b[i] + 1 });
	}
	ll carry = 0, mul = 1, ans = 0;
	for (int i = ma - 1; i >= 0; --i) {
		c[i] = a[i] - carry - b[i];
		if (c[i] < 0) {
			carry = 1;
			c[i] += q[i];
		}
		else {
			carry = 0;
		}
		ans = (ans + c[i] * mul) % 1000000007;
		mul = (mul * q[i]) % 1000000007;
	}

	cout << ans;
	return 0;
}

试题 F: 统计子矩阵

方法一：前缀和 + 双指针

枚举右下角坐标，用双指针找出左上的端点范围，计算可行的矩阵数量

#include
using namespace std;

static int stream_off = []() {
	std::ios::sync_with_stdio(false);
	cin.tie(NULL);
	return 0;
}();//关闭流同步，注意不要和c式输入同时使用（如快读板子）


using ll = long long;
using ull = unsigned long long;
ll v[501][501]{};
int main() {
	int n, m;
	ll k;
	cin >> n >> m >> k;

	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) {
			cin >> v[i][j];
			v[i][j] += v[i - 1][j] + v[i][j - 1] - v[i - 1][j - 1];
		}
	}
	ll ans = 0;
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= m; ++j) {
			int x = i - 1, y = 0;
			while (x >= 0 && y < j) {
				ll s = v[i][j] - v[i][y] - v[x][j] + v[x][y];
				while (s > k) {
					++y;
					s = v[i][j] - v[i][y] - v[x][j] + v[x][y];
				}
				ans += j - y;
				--x;
			}
		}
	}
	cout << ans;
	return 0;
}

复杂度分析

• 时间复杂度 $O(mn(m+n))$ 每一个右下角端点， 双指针最多移动 $m+n$ 次
• 空间复杂度 $O(mn)$

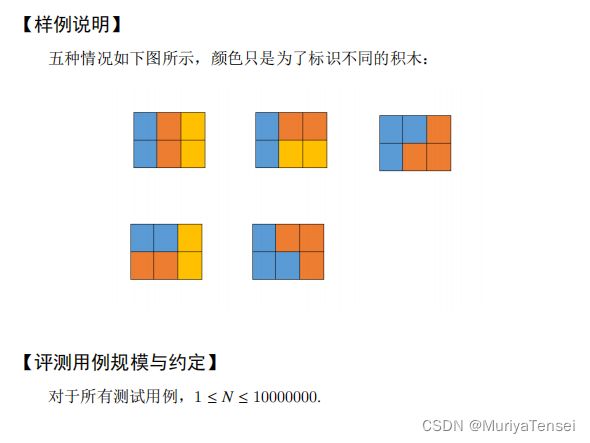
试题 G: 积木画

方法一：动态规划

设 $f(n)$ 为 $2\ast n$ 大小的画布可行的方法数
自己画一画就能发现，
多一行可以加一块，
多两行可以立着的两块（另一个方向在多一行的部分计算过了）
多一行半加一块L

而一行半结尾的情况，又由 整行+L或 半行+I 转移而来

因此有

$f(x)=f(x-1)+f(x-2)+g(x-2)$
$g(x)=g(x-1)+f(x-1)\ast 2$

注意转移然后取模即可

#include
using namespace std;
using ll = long long;
using ull = unsigned long long;
int main() {
	ll n;
	cin >> n;
	vector<ll> dp(n + 1), dpc(n + 1);
	dp[0] = 0, dp[1] = 1, dp[2] = 2;
	dpc[0] = 0, dpc[1] = 2, dpc[2] = 4;
	for (int i = 3; i <= n; ++i) {
		dp[i] = (dp[i - 1] + dp[i - 2] + dpc[i - 2]) % 1000000007;
		dpc[i] = (dpc[i - 1] + dp[i - 1] * 2) % 1000000007;
	}
	cout << dp[n] << endl;
	return 0;
}

复杂度分析

• 时间复杂度 $O(n)$
• 空间复杂度 $O(n)$

空间优化

可以进行如下空间优化，使得空间化为 $O(1)$

#include
using namespace std;
using ll = long long;
using ull = unsigned long long;
int main() {
	ll n;
	cin >> n;
	ll x0 = 1, x1 = 1, x2, y0 = 0, y1;
	while (--n) {
		x2 = (x1 + x0 + y0) % 1000000007;
		y1 = (y0 + x0 * 2) % 1000000007;

		x0 = x1;
		x1 = x2;
		y0 = y1;
	}
	cout << x1;
	return 0;
}

方法二：动态规划优化

把方法一中的式子化简

把②式不断代入①式消去g, 再把得到的式子③中的x替换为x-1得到④
③④左右分别作差后化简即可得到如下式子

$f(n)=f(n-1)\ast 2+f(n-3)$

#include
using namespace std;
using ll = long long;
using ull = unsigned long long;
int main() {
	ll n, a = 0, b = 1, c = 1, d = 1;
	cin >> n;
	ll t = n;
	while (--t) {
		d = (c + c + a) % 1000000007;
		a = b;
		b = c;
		c = d;
	}
	cout << d << endl;
	return 0;
}

复杂度分析

• 时间复杂度 $O(n)$
• 空间复杂度 $O(1)$

方法三：矩阵快速幂

化简后的式子就可以用矩阵快速幂进行进一步优化（不过本题数据量1e7应该没太大必要）

#include

template<typename size_type = uint64_t, size_type MOD = 1000000007>
class matrix_t {
public:
    int n, m;
    std::vector<std::vector<size_type> > nums;

    /* 方阵/单位矩阵 ;fillFlag = 1时 构造单位矩阵， 在对角线填充FillChar */
    matrix_t(const int n = 0, bool fillFlag = 1, int fillChar = 1) :nums(n, std::vector<size_type>(n)), n(n), m(n) {
        if (fillFlag == 1) for (int i = 0; i < n; ++i) nums[i][i] = fillChar;
    }

    /* 一般矩阵 */
    matrix_t(const int n, const int m) : n(n), m(m), nums(n, std::vector<size_type>(m)) {}

    /* 邻接矩阵 */
    matrix_t(const std::vector<std::vector<int>>& relation, const int n) :nums(n, std::vector<size_type>(n)), n(n), m(n) {
        for (auto&& ns : relation) nums[ns[0]][ns[1]] = 1;
    }

    /* 数组构造矩阵 */
    matrix_t(const std::vector<std::vector<size_type>>& relation) :n(relation.size()), m(relation.front().size()), nums(relation) { }

    matrix_t operator * (const matrix_t& other)const {
        if (this->m != other.n) throw std::string("矩阵乘法长宽不符");
        matrix_t ret(this->n, other.m);
        for (int x = 0; x < this->n; ++x)
            for (int y = 0; y < other.m; ++y)
                for (int k = 0; k < this->m; ++k)
                    ret.nums[x][y] = (ret.nums[x][y] + this->nums[x][k] * other.nums[k][y]) % MOD;
        return std::move(ret);
    }

    template<typename T>
    matrix_t pow(T k)const {
        matrix_t e(n), ans(e), base(*this);
        while (k) {
            if (k & 1) ans = ans * base;
            base = base * base;
            k >>= 1;
        }
        return std::move(ans);
    }

    template<typename T>
    matrix_t operator ^ (T k)const {
        return std::move(this->pow(k));
    }

    size_type __sums() {
        size_type ret{};
        for (auto&& x : nums) for (auto&& v : x) ret = (ret + v) % MOD;
        return ret;
    }

    inline size_type& set(int x, int y, size_type v) {
        return nums[x][y] = v;
    }

    std::vector<size_type>& operator [] (int x) {
        return nums[x];
    }
};
template<typename size_type = uint64_t, size_type MOD = 1000000007>
using __mat_t = matrix_t<size_type, MOD>;
using namespace std;
using ll = long long;
using ull = unsigned long long;
int main() {
	vector<vector<ll> > vb{ {1,1,2} }, ve{ {0,0,1},{1,0,0}, {0,1,2} };
	__mat_t<ll, 1000000007> b(vb), e(ve);
	int n;
	cin >> n;
	cout << (b * (e ^ n))[0][0] << endl;
	return 0;
}

复杂度分析

• 时间复杂度 $O(log(n))$ 实际上常数为运算四阶矩阵乘法所需 $O(4^3)$
• 空间复杂度 $O(1)$实际上常数为储存四阶矩阵乘法所需

试题 H: 扫雷

方法一：BFS + 哈希表（待优化）

模拟了下，似乎常数太大了，试了一个小时没降下去，极限用例无论如何都要 20s+（而民间测试中，应该是随机数据，可以极限过）
这里直接跑的BFS，但是还是差点意思，优化了好久
试过在map上二分优化，但是map又不能在查找过程中删除（会导致迭代器失效），所以效果比较有限

但是总感觉不应该爆，有没有大佬帮忙挑挑问题，是不是哪里删除失效了，或者错误插入了导致破坏了线性复杂度

感觉做的很暴力，极限对于半径均为10的5e4个雷和火箭 就会超时
最好的优化方法应该是自己手写哈希，大概能快10~30倍左右，就没问题了（蠢了，STL玩太多）

#include

namespace std {
	template <typename T>
	struct hash<pair<T, T>> {
		size_t operator()(const pair<T, T>& p) const noexcept {
			return hash<T>()(p.first) ^ hash<T>()(p.second);
		}
	};
}
using namespace std;

/*

 */

using ll = long long;
using ull = unsigned long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using db = double;


inline long long read() {
	long long o = 0, f = 1; char c = getchar();
	while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar(); }
	while (c > '/' && c < ':') { o = o * 10 + c - '0'; c = getchar(); }
	return o * f;
}

inline void writeLL(long long x) {
	if (x < 0) {
		putchar('-');
		writeLL(-x);
	}
	if (x > 9LL) writeLL(x / 10LL);
	putchar(x % 10 + 48);
}

int main() {
	int n, m;
	n = read(), m = read();
	unordered_map < ll, unordered_map<ll, pair<ll, int> > > s;
	ll x, y, r;
	for (int i = 0; i < n; ++i) {
		x = read(), y = read(), r = read();
		auto&& q = s[x][y];
		q.first = max(q.first, r);
		++q.second;
	}
	int ans = 0;
	function<int(ll, ll)> exp = [&](ll rx, ll ry) -> int {
		deque<pll> dq;
		deque<pll> dr;
		dq.emplace_back(rx, ry);
		dr.emplace_back(s[rx][ry]);
		s[rx].erase(ry);
		if (s[rx].empty()) s.erase(rx);
		int ret = 0;
		while (dq.size()) {
			ll x = dq.front().first, y = dq.front().second;
			ll r = dr.front().first;
			ret += dr.front().second;
			dq.pop_front();
			dr.pop_front();

			for (int i = -r; i <= r; ++i) {
				for (int j = -r; j <= r; ++j) {
					if (i * i + j * j > r * r) continue;
					ll nx = x + i, ny = y + j;
					if (s.count(nx) == 0 || s[nx].count(ny) == 0) continue;
					dq.emplace_back(nx, ny);
					dr.emplace_back(s[nx][ny]);
					s[nx].erase(ny);
					if (s[nx].empty()) s.erase(nx);
				}
			}
		}
		return ret;
	};
	for (int i = 0; i < m; ++i) {
		x = read(), y = read(), r = read();
		auto&& q = s[x][y];
		q.first = max(q.first, r);
		ans += exp(x, y);
	}
	writeLL(ans);
	return 0;
}

复杂度分析

• 时间复杂度 $O((m+n)\ast r^2)$ 至多遍历每个点(包括地雷和火箭)及其周围r^2的区域
• 空间复杂度 $O(m+n)$

试题 I: 李白打酒加强版

方法一：动态规划

三维dp，$dp[i][j][k]$ 表示 剩余 $i$ 次店、$j$ 次花 时 有 $k$ 斗酒 的方法数
转移方法如代码所示，非常好理解

注意：最后返回的是 dp[0][1][1] 因为最后一次是花，因此最后剩余1次花1斗酒

这里懒得用vector开三维数组了，c++11自推导模板类型太菜了，写起来好麻烦，直接开全局数组了。
如果支持c++14我就继续vector了，开成 n+1 m+1 m+1三维即可

#include
using namespace std;
using ll = long long;
ll dp[105][105][105]{};
int main() {
	int n, m;
	cin >> n >> m;
	ll MOD = 1000000007;
	dp[n][m][2] = 1;
	for (int i = n; i >= 0; --i) {
		for (int j = m; j >= 0; --j) {
			for (int k = m; k >= 0; --k) {
				if (i > 0 && k + k <= m) {
					dp[i - 1][j][k + k] = (dp[i - 1][j][k + k] + dp[i][j][k]) % MOD;
				}
				if (j > 0 && k > 0) {
					dp[i][j - 1][k - 1] = (dp[i][j - 1][k - 1] + dp[i][j][k]) % MOD;
				}
			}
		}
	}
	cout << (dp[0][1][1] % MOD) << endl;
	return 0;
}

复杂度分析

• 时间复杂度 $O(n{m}^2)$ 注意到，酒的数量不能超过花（不然喝不完）因此，酒这一维上限与花一样即可
• 空间复杂度 $O(n{m}^2)$

试题 J: 砍竹子

不确定对不对，做的时候写错了个函数名，直接g了（样例过了，我自己测了两组也过了，但是考完又造了一组wa了……）

注意到，（数据范围内）最大的数 运行转换至多七次可以到1

那么我们处理出所有数字转化的路线，从小到大 合并连续相同的部分即可

方法一：逆向思维

#include
using namespace std;

using ll = long long;
using ull = unsigned long long;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using db = double;


static int stream_off = []() {
	std::ios::sync_with_stdio(false);
	cin.tie(NULL);
	return 0;
}();//关闭流同步，注意不要和c式输入同时使用（如快读板子）

ll fuc(ll x) {
	return sqrt(x / 2 + 1);
}

int main() {
	int n;
	cin >> n;
	ll ans = 0;
	vector<vector<ll> > v(n);
	for (int i = 0; i < n; ++i) {
		ll x;
		cin >> x;
		while (x > 1) {
			v[i].push_back(x);
			x = fuc(x);
		}
		reverse(v[i].begin(), v[i].end());
	}
	for (int step = 0; step < 7; ++step) {
		ll rear = -1;
		for (auto& x : v) {
			if (x.size() <= step) {
				rear = -1;
				continue;
			}
			if (x[step] != rear) ++ans;
			rear = x[step];
		}
	}
	cout << ans;
	return 0;
}

复杂度分析

• 时间复杂度 $O(n)$ 这里把7次视为常数了，因为数据范围是固定的
• 空间复杂度 $O(n)$